15.Функциональный ряд Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция .Функциональный ряд

 — n-ная частичная сумма.

Сходимость

Ряд называется сходящимся поточечно, если последовательность   его частичных сумм сходится поточечно.

Ряд называется сходящимся равномерно, если последовательность   его частичных сумм сходится равномерно.

Необходимое условие равномерной сходимости

Критерий Коши равномерной сходимости

Критерий Коши для последовательности  . Чтобы последовательность функций  , определенных на множестве  , равномерно сходилась на этом множестве, необходимо и достаточно, чтобы для всякого   существовал номер  , такой, что при всех   больше либо равных   одновременно для всех   выполнялось неравенство 

Абсолютная и условная сходимость

Ряд   называется абсолютно сходящимся, если   сходится. Абсолютно сходящийся ряд сходится.

Если ряд   сходится, а   расходится, то ряд   называется сходящимся условно. Для таких рядов верна теорема Римана о перестановке членов условно сходящегося ряда.

Признаки равномерной сходимости

Признак сравнения

Ряд   сходится абсолютно и равномерно, если выполнены условия:

1. Ряд 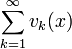  сходится равномерно.

2. 

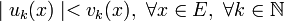
Частным случаем является признак Вейерштрасса, когда  . Таким образом функциональный ряд ограничиваеся обычным. От него требуется обычная сходимость

Признак Дирихле

Ряд   сходится равномерно, если выполнены следующие условия:

1. Последовательность действительнозначных функций   монотонна 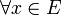  и 

2. Частичные суммы   ряда   равномерно ограничены.

Признак Абеля

Ряд   сходится равномерно, если выполнены следующие условия:

1. Последовательность действительнозначных функций   равномерно ограничена и монотонна  .

2. Ряд   равномерно сходится.

Свойства равномерно сходящихся последовательностей и рядов

Теоремы о непрерывности

Рассматриваются комплекснозначные функции на множестве 

Последовательность непрерывных в точке функций сходится к функции непрерывной в этой точке.

Последовательность 

 функция   непрерывна в точке 

Тогда   непрерывна в  .

Ряд непрерывных в точке функций сходится к функции непрерывной в этой точке.

Ряд 

 функция   непрерывна в точке 

Тогда   непрерывна в  .

Теоремы об интегрировании

Рассматриваются действительнозначные функции на отрезке действительной оси.

Теорема о переходе к пределу под знаком интеграла.

 функция   непрерывна на отрезке 

 на 

Тогда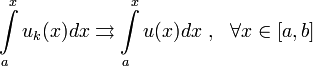 

Теорема о почленном интегрировании.

 функция   непрерывна на отрезке 

 на 

Тогда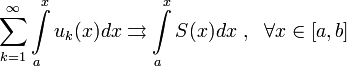 

Теоремы о дифференцировании

Рассматриваются действительнозначные функции на отрезке действительной оси.

Теорема о дифференцировании под пределом.

 функция   непрерывно дифференцируема на отрезке 

 сходится

 на отрезке 

Тогда   — непрерывно дифференцируема на  ,   на 

Теорема о почленном дифференцировании.

 функция   непрерывно дифференцируема на отрезке 

 сходится

 равномерно сходится на отрезке 

Тогда   — непрерывно дифференцируема на  ,   на