
- •Изложены методические рекомендации, задания для самостоятельной работы и образцы решения задач по теме: «Симплексный метод в решении задач линейного программирования»
- •« Симплексный метод в решении задач линейного программирования»
- •212005, Г. Могилев, пр. Мира,43
- •Обыкновенные и модифицированные жордановы исключения
- •Задачи для самостоятельного решения
- •Базисные и опорные решения системы линейных уравнений
- •Задачи для самостоятельного решения
- •Основная идея и алгоритм симплексного метода
- •Список литературы
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ»
Кафедра «Высшая математика»
Методические указания к изучению темы
« Симплексный метод в решении задач линейного программирования»
для студентов экономических специальностей
дневной и заочной форм обучения

Могилев 2010
УДК 517
ББК 221
Л 59
Рекомендовано к опубликованию
учебно-методическим управлением
ГУВПО «Белорусско-Российский университет»
Одобрено кафедрой «Высшая математика» « 15» января 2010 г.,
протокол №4
Составители: канд. физ.-мат. наук, доц. Данилович Л. А.,
ст. преп. Бутома А. М.
Рецензент канд. физ.-мат. наук, доц. Л. В. Плетнев
Изложены методические рекомендации, задания для самостоятельной работы и образцы решения задач по теме: «Симплексный метод в решении задач линейного программирования»
Учебное издание
ВЫСШАЯ МАТЕМАТИКА
« Симплексный метод в решении задач линейного программирования»
Ответственный за выпуск Л. В. Плетнев
Технический редактор А. Т. Червинская
Компьютерная верстка Н. П. Полевничая
Подписано в печать . Формат 6084/16. Бумага офсетная. Гарнитура Таймс.
Печать трафаретная. Усл. печ. л. . Уч.-изд. л. . Тираж 215 экз. Заказ №
Издатель и полиграфическое исполнение
Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет»
ЛИ № 02330/375 от 29.06.2004 г.
212005, Г. Могилев, пр. Мира,43
© ГУ ВПО «Белорусско-Российский
университет», 2010
Обыкновенные и модифицированные жордановы исключения
Рассмотрим одно алгебраическое преобразование, лежащее в основе удобного вычислительного аппарата, используемого в математическом программировании.
Пусть дана система
 линейных функций)
линейных функций)
 от
от
 неизвестных
неизвестных
 :
:
 ,
(1)
,
(1)
где
 ─
постоянные величины
─
постоянные величины
 .
.
Представим систему (1.1) в форме таблицы 1.
Таблица 1.
|
|
… |
|
… |
|
… |
|
|
|
… |
|
… |
|
… |
|
… |
........................................................................................................................ |
||||||
|
|
… |
|
… |
|
… |
|
… |
……………………………………………………………………………… |
||||||
|
|
… |
|
… |
|
… |
|
… |
……………………………………………………………………………… |
||||||
|
|
… |
|
… |
|
… |
|
Таблицу 1 в дальнейшем
будем называть жордановой.
От табличной записи легко перейти к
обычной записи системы. Для этого надо
умножить элементы
 й
строки на соответствующие неизвестные
,
стоящие в верхней заглавной строке,
полученные произведения сложить и сумму
приравнять к
й
строки на соответствующие неизвестные
,
стоящие в верхней заглавной строке,
полученные произведения сложить и сумму
приравнять к
 .
.
Выберем из системы
(1) какое-либо уравнение, например
 е:
е:
 ,
(2)
,
(2)
и предположим, что
коэффициент при
в уравнении (2) отличен от нуля, т.е.
 .
Затем представим себе схематизированную
алгебраическую операцию перераспределения
ролей между зависимой переменной
.
Затем представим себе схематизированную
алгебраическую операцию перераспределения
ролей между зависимой переменной
 и независимой
,
т.е. операцию решения уравнения
относительно переменной
:
и независимой
,
т.е. операцию решения уравнения
относительно переменной
:
 ,
(3)
,
(3)
подстановки
полученного выражения (3) во все остальные
уравнения системы (1), приведения подобных
членов и записи преобразованной таким
образом системы в форме жордановой
таблицы. Описанную операцию будем
называть шагом
обыкновенного жорданова исключения,
произведенным
над таблицей 1 с разрешающим элементом
,
с
й
разрешающей строкой и
 м
разрешающим столбцом.
м
разрешающим столбцом.
Выясним, как преобразуются элементы таблицы 1 в результате шага обыкновенного жорданова исключения. С этой целью значение из выражения (3) подставим в остальные равенства системы (1) и выполним необходимые преобразования:
 .
(4)
.
(4)
Обозначим в системе (4)

 .
(5)
.
(5)
Тогда система (4) запишется в виде
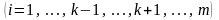 .
(6)
.
(6)
Преобразованную систему (3),(6) перепишем в форме жордановой таблицы (таблица 2).
Таблица 2
|
|
… |
|
… |
|
|
|
… |
|
… |
|
… |
……………………………………………………………………………. |
||||
|
|
… |
|
… |
|
… |
…………………………………………………………………………… |
||||
|
|
… |
|
… |
|
Сопоставляя таблицы 1 и 2, нетрудно заметить, что один шаг обыкновенного жорданова исключения с разрешающим элементом переводит таблицу 1 в новую таблицу 2 по схеме, состоящей из следующих четырех правил:
1) разрешающий элемент заменяется обратной величиной;
2) остальные элементы разрешающей строки делят на разрешающий элемент и меняют знаки;
3) остальные элементы разрешающего столбца делят на разрешающий элемент;
4) прочие элементы вычисляют по формуле (5).
На практике при вычислении элементов по формуле (5) удобно пользоваться правилом прямоугольника. Чтобы выяснить его суть, рассмотрим фрагмент таблицы 1, содержащий элементы, входящие в формулу (5):
-
………………………………
…
…
…
……………………………….
…
…
…
……………………………….
Они расположены
в вершинах воображаемого «прямоугольника».
Диагональ этого прямоугольника, на
которой расположены разрешающий
и преобразуемый
элементы, назовем главной,
а другую диагональ ─ побочной.
Тогда из формулы (5) непосредственно
следует, что преобразованный
элемент
 равен разности
произведений элементов, расположенных
на главной и побочной диагоналях,
деленной на разрешающий элемент.
равен разности
произведений элементов, расположенных
на главной и побочной диагоналях,
деленной на разрешающий элемент.
Сформулированного правила следует придерживаться независимо от того, в какой вершине прямоугольника расположен разрешающий элемент.
Из формулы (5)
видно, что если в разрешающей строке
некоторый элемент
 ,
то
,
то
 ,
т.е. элементы столбца, в котором расположен
нулевой элемент разрешающей строки,
остаются после шага жорданова исключения
без изменения. Аналогично: если в
разрешающем столбце есть нулевой элемент
,
т.е. элементы столбца, в котором расположен
нулевой элемент разрешающей строки,
остаются после шага жорданова исключения
без изменения. Аналогично: если в
разрешающем столбце есть нулевой элемент
 ,
то соответствующая ему строка остается
на данном шаге неизменной, так как
.
,
то соответствующая ему строка остается
на данном шаге неизменной, так как
.
Вместо обыкновенных часто пользуются так называемыми модифицированными жордановыми исключениями, при которых система (1) записывается в форме жордановой таблицы 3, отличающейся от таблицы 1 тем, что переменные в заглавной строке записаны со знаком “минус”.
Таблица 3.
|
|
…
|
………………………..
|
Можно показать, что один шаг модифицированного жорданова исключения переводит таблицу 3 в новую таблицу по следующим правилам:
1) разрешающий элемент заменяется обратной величиной;
2) остальные элементы разрешающей строки делят на разрешающий элемент;
3) остальные элементы разрешающего столбца делят на разрешающий элемент и меняют знаки;
4) прочие элементы вычисляют по формуле (5).
Решение систем линейных уравнений
Рассмотрим систему линейных уравнений с неизвестными
 (7)
(7)
Пусть ранг матрицы
коэффициентов

 равен
равен
 .
Перепишем уравнения системы (7) в форме
нуль-равенств
.
Перепишем уравнения системы (7) в форме
нуль-равенств

и полученную систему запишем в жорданову таблицу (таблица 4).
Таблица 4.
|
1 |
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
… |
|
|
|
… |
|
Над таблицей 4 можно произвести лишь последовательных жордановых исключений. В результате получится, например, таблица 5.
Таблица 5.
|
1 |
|
… |
|
|
… |
|
|
|
|
… |
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
|
… |
|
|
|
|
… |
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
|
… |
|
Система (7) совместна тогда и только тогда, когда для некоторой совокупности значений выполняются одновременно все равенства (7). Это возможно в том и только в том случае, если в таблице 5
=…= = .
Если хотя бы один из свободных членов ,…, отличен от нуля, то система (7) несовместна.
В случае совместности системы из таблицы 5 получаем общее решение системы (7):
 (8)
(8)
При решении задач столбцы под переброшенными в верхнюю часть таблицы нулями (а такими столбцами являются разрешающие) опускают за ненадобностью.
Придавая в
равенствах (8) переменным
 произвольные числовые значения
произвольные числовые значения
 ,
вычисляют соответствующие значения
остальных неизвестных:
,
вычисляют соответствующие значения
остальных неизвестных:

и тем самым получают
частное решение
 системы (7). Таким путем можно найти
бесконечное множество решений системы
(7).
системы (7). Таким путем можно найти
бесконечное множество решений системы
(7).
В частном случае,
когда
 ,
через
шагов жордановых исключений все
переменные
,
через
шагов жордановых исключений все
переменные
 окажутся в левом заглавном столбце
таблицы 5, а их место наверху таблицы
займут нули, поэтому система (7) будет
иметь единственное решение:
окажутся в левом заглавном столбце
таблицы 5, а их место наверху таблицы
займут нули, поэтому система (7) будет
иметь единственное решение:
 .
.
Итак, для решения системы линейных уравнений ее надо записать в форме жордановой таблицы и проделать возможное число шагов жордановых исключений, вычеркивая после каждого шага разрешающий столбец и строки, если они целиком состоят из нулевых элементов. Если в ходе исключений появится строка, все элементы которой, кроме свободного члена, равны нулю, то данная система несовместна. В противном случае система совместна. При этом она имеет бесконечное множество решений, если в верхней заглавной строке последней жордановой таблицы останется хотя бы одна переменная, и единственное решение, если все переменные окажутся в левом заглавном столбце.
Пример 1. Найти решение системы:

Решение: Запишем систему в виде жордановой таблицы и сделаем два шага жордановых исключений (табл.68).
Таблица 6.
|
1 |
|
0= |
3 |
1 2 1 6 |
0= |
0 |
1 1 1 4 |
0= |
3 |
1 0 1 2 |
|
|
|
Таблица 7. |
|
|
|
1 |
|
0= |
3 |
1 1 2 |
x2 |
0 |
1 1 4 |
0= |
3 |
1 1 2 |
Таблица 8. |
|
|
|
1 |
|
0= |
0 |
0 0 |
x2 = |
3 |
0 2 |
x1 = |
3 |
1 2 |
При практическом решении задач столбцы под переброшенными наверх таблицы нулями (и такими столбцами являются разрешающие) опускают за ненадобностью.
Из таблицы 8 выпишем общее решение системы:

где х3 и х4 могут принимать любые значения.
































 …
…

























 =
=
