Вопросы для зачёта 1.
Математическое ожидание дискретной случайной величины и его свойства.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Если дискретная случайная величина принимает только значения x1, x2, ..., xn, вероятности которых соответственно равны p1, p2, ..., pn . Тогда математическим ожидание определяется равенством:
M (X) = x1p1 + x2p2 + ...+ xnpn. (3.1)
Если дискретная случайная величина принимает счетное множество возможных значений, то
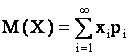(3.2)
Свойства математического ожидания случайной величины:
1. Математическое ожидание постоянной величины равно самой величине:
М[C]=C.
2. Постоянный множитель можно выносить за знак математического ожидания:
М[C×Х]=C×M[X].
3. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин:
М[Х+Y]=M[X]+M[Y].
4. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин:
М[Х×Y]=M[X]×M[Y].
(Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения принимает другая величина.)
На практике часто приходится оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.
Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D[Х] = М[(Х – М[Х])2]. (6.4)
Рассмотрим дискретную случайную величину Х, принимающую значения , , …, с вероятностями , , …,. Используя в выражении (6.4) определение математического ожидания (6.3), получим следующую формулу для вычисления дисперсии:
D[Х] =
=
×p1+
×p2+…+
×p.
Для вычисления дисперсии также можно пользоваться следующей формулой:
D[Х] = М[Х2] – (М[Х])2. (6.6)
Докажем формулу (6.6). Раскрыв квадрат разности, получим:
D[Х] = М[(Х – М[Х])2] = М[Х2 – 2×Х×М[Х]+ М[Х]2].
Учитывая, что М[Х] – это некоторое постоянное число, раскроем предыдущее равенство так: D[Х] = М[Х2]–M[2×Х×М[Х]]+M[М[Х]2] = М[Х2]– 2×(М[Х])2 +(М[Х])2 = М[Х2] – (М[Х])2.
Свойства дисперсии случайной величины:
1. Дисперсия постоянной величины равна нулю:
D[C]=0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D[C×Х]=C2×M[X].
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D[Х+Y]=D[X]+D[Y].
4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин:
D[Х–Y]=D[X]+D[Y].
Средним квадратическим отклонением случайной величины Х называется корень квадратный из ее дисперсии:
Числовые характеристики непрерывных случайных величин.
При введении понятия математического ожидания воспользуемся понятием элемента вероятности
р(х) Dх.
Предположим, что все возможные значения случайной величины Х принадлежат отрезку [а, b]. Разобьем произвольным образом этот отрезок точками а=x0<x1<x2<…<xn=b на п частичных отрезков. В каждом таком частичном отрезке, длина которого D х,, произвольно возьмем точку hi, где i=l, 2, 3, ..., п. Известно, что вероятность попадания значения непрерывной случайной величины на отрезок Dх приближенно равна р(х)Dx (элемент вероятности) и поэтому приближенно будем считать, что случайная величина Х может принять n значений hi на отрезке [а, b] с вероятностями р(hi) Dxi. Теперь можно воспользоваться формулой, задающей математическое ожидание для дискретной случайной величины. В результате будем иметь
Переходя к пределу в правой части равенства, имеем:
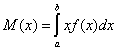
Определение. Математическим ожиданием M(X) непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл
Если возможные значения случайной величины распределены по всей оси Ох, то
Здесь предполагается, что несобственный интеграл сходится абсолютно, т. е. существует.
Т.к. дисперсия случайной величины есть математическое ожидание квадрата отклонения случайной величины от своего математического ожидания, то
Дисперсией непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл
При вычислении дисперсии НСВХ также можно пользоваться формулой
Среднее квадратическое отклонение равно корню квадратному из дисперсии
