
4. Приближенное решение обыкновенных дифференциальных уравнений.
Метод Эйлера численного интегрирования
обыкновенных дифферинциальных уравнений.
Для приближенного
решения дифференциального уравнения
![]() с
начальным условием
с
начальным условием
![]() Расчетная
формула
Расчетная
формула![]()
Пример1 Для уравнения
![]() при
начальном условии
при
начальном условии
![]() с
шагом
h =
0,1 значение
с
шагом
h =
0,1 значение
![]() с
точностью до сотых равно …
Решение:
Найдем
значения:
с
точностью до сотых равно …
Решение:
Найдем
значения:
![]()
![]()
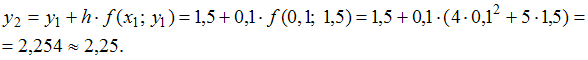 Тогда
получим:
Тогда
получим:
![]()
Пример. На отрезке 0;0,5 вычислить с шагом h=0,1 интеграл уравнения y’=x+y, если y(0)=1.
xi |
yi |
y’=xi+yi |
hf(xi,yi)=hy’ |
0 |
1 |
1 |
0,1 |
0,1 |
1,1 |
1,2 |
0,12 |
0,2 |
1,22 |
1,42 |
0,142 |
0,3 |
1,362 |
1,662 |
0,1662 |
0,4 |
1,5282 |
1,9282 |
0,19282 |
0,5 |
1,72102 |
|
|
Тогда для уравнения
 при
начальном условии
с
шагом
h =
0,1 значение
с
точностью до сотых равно …
при
начальном условии
с
шагом
h =
0,1 значение
с
точностью до сотых равно …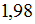
для уравнения
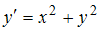 при
начальном условии
с
шагом
при
начальном условии
с
шагом
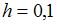 и
с точностью до сотых
равно …1,22
и
с точностью до сотых
равно …1,22
для уравнения
 при
начальном условии
с
шагом
и
точностью до сотых
равно …1,23
при
начальном условии
с
шагом
и
точностью до сотых
равно …1,23
Для приближенного вычисления
определенного интеграла от функции
можно
воспользоваться формулой трапеций
 и
вычислили
пример2
и
вычислили
пример2
 Интервал
Интервал
![]() разбили
на 4 равные части … Решение:
Отрезок
разбит
на 4 равные части, с шагом
разбили
на 4 равные части … Решение:
Отрезок
разбит
на 4 равные части, с шагом
![]() Получили:
Получили:
![]() соответствующие приближенные значения
соответствующие приближенные значения
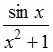 .:
.:
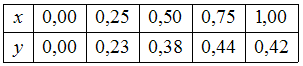 .,т.е.
.,т.е.
![]()
![]()
![]()
![]()
![]() По
формуле трапеций имеем:
По
формуле трапеций имеем:
Для приближенного вычисления определенного интеграла от функции
 на
интервале
можно
воспользоваться формулой трапеций Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения функции
.
на
интервале
можно
воспользоваться формулой трапеций Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения функции
.
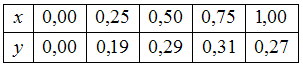 ,
тогда
,
тогда
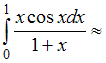 …0,23
…0,23Для приближенного вычисления определенного интеграла от функции
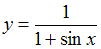 на
интервале
можно
воспользоваться формулой трапеций. Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения функции
.
на
интервале
можно
воспользоваться формулой трапеций. Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения функции
.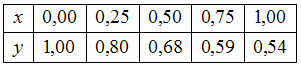 ,тогда
,тогда
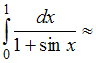 … 0,71
… 0,71Для приближенного вычисления определенного интеграла от функции
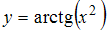 на
интервале
на
интервале
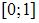 можно
воспользоваться формулой трапеций
Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения
можно
воспользоваться формулой трапеций
Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения
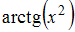 :
: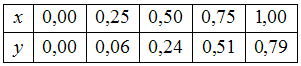 Тогда
Тогда
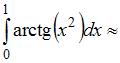 …0,30
…0,30
6. Численное дифференцирование.
Интерполяционные формулы
Интерполяционные формулы — в
математике формулы, дающие приближённое
выражение функции
![]() при
помощи интерполяции,
то есть через интерполяционный многочлен
при
помощи интерполяции,
то есть через интерполяционный многочлен
![]() степени
степени
![]() ,
значения которого в заданных точках
,
значения которого в заданных точках
![]() совпадают
со значениями
совпадают
со значениями
![]() функции
функции
![]() в
этих точках. Многочлен
определяется
единственным образом, но в зависимости
от задачи его удобно записывать различными
по виду формулами.
в
этих точках. Многочлен
определяется
единственным образом, но в зависимости
от задачи его удобно записывать различными
по виду формулами.
|
|
Интерполяционная формула Лагранжа
Функция
![]() может
быть интерполирована на отрезке
может
быть интерполирована на отрезке
![]() интерполяционным
многочленом
,
записанным в форме Лагранжа:
интерполяционным
многочленом
,
записанным в форме Лагранжа:
![]()
Интерполяционная формула Ньютона
Если точки
расположены
на равных расстояниях
![]() ,
многочлен
можно
записать так:
,
многочлен
можно
записать так:
![]()
(здесь
![]() ,
а
,
а
![]() —
разности k-го порядка:
—
разности k-го порядка:
![]() ).
Это так называемая формула Ньютона для
интерполирования вперёд; название
формулы указывает на то, что она содержит
заданные значения
).
Это так называемая формула Ньютона для
интерполирования вперёд; название
формулы указывает на то, что она содержит
заданные значения
![]() ,
соответствующие узлам интерполяции,
находящимся только вправо от
,
соответствующие узлам интерполяции,
находящимся только вправо от
![]() .
Эта формула удобна при интерполировании
функций для значений
.
Эта формула удобна при интерполировании
функций для значений
![]() ,
близких к
.
Если требуется
найти значение производной данной
функции
в некоторой точке, то можно
заменить данную, аналитическая запись
которой неизвестна, некоторой другой
функцией
,
близких к
.
Если требуется
найти значение производной данной
функции
в некоторой точке, то можно
заменить данную, аналитическая запись
которой неизвестна, некоторой другой
функцией
![]() для
которой
для
которой
![]() и
найти производную функции
и
найти производную функции
![]() Если
шаг таблицы h
(разность между соседними значениями
x)
является величиной постоянной, то можно
воспользоваться формулой
Если
шаг таблицы h
(разность между соседними значениями
x)
является величиной постоянной, то можно
воспользоваться формулой
Пример1.Некоторая
функция
![]() задана
в виде таблицы
задана
в виде таблицы
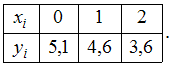 Найдите
Найдите
![]() …
…
Решение:
Напоминаем,
что
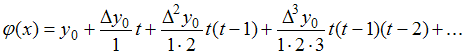 ,
где
,
где
![]() .
Тогда
.
Тогда
 .
.
![]() ;
;
![]()
![]() .
.
![]() .
.
![]()
Пример2 Некоторая
функция
задана
в виде таблицы
 Для
заданной в виде таблицы функции
значение
Для
заданной в виде таблицы функции
значение
![]() …
Вычисления производите с двумя знаками
после запятой. Решение:
Напоминаем,
что
…
Вычисления производите с двумя знаками
после запятой. Решение:
Напоминаем,
что
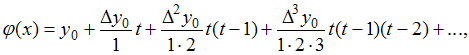 где
где
![]() Тогда
Тогда
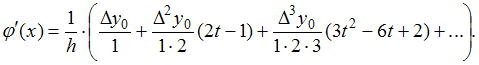
![]()
![]()
![]()
![]()
![]()
Некоторая функция задана в виде таблицы
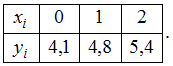 где
где
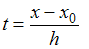 и
и
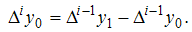 Вычисления
производите с двумя знаками после
запятой. Для заданной в виде таблицы
функции
значение
…0,76
Вычисления
производите с двумя знаками после
запятой. Для заданной в виде таблицы
функции
значение
…0,76Некоторая функция задана в виде таблицы
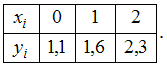 Для
заданной в виде таблицы функции
значение
…0,56
Для
заданной в виде таблицы функции
значение
…0,56Некоторая функция задана в виде таблицы
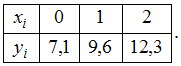 Для
заданной в виде таблицы функции
значение
…2,58
Для
заданной в виде таблицы функции
значение
…2,58
ИТОГОВЫЙ ТЕСТ ПО ТЕМЕ: «Основные численные методы»
1. Если число 2,5 округлить до 3, тогда относительная погрешность полученного приближенного числа будет равна:
1) 0,5 2) 0,2 (и) 3) -0,2 4) -0,5
2. Вычислили значение функции
![]() при
при
![]() и
и
![]() получили
результат равный 800. Известны относительные
погрешности чисел 10 и 2:
получили
результат равный 800. Известны относительные
погрешности чисел 10 и 2:
![]() Тогда
относительная погрешность полученного
результата равна …
Тогда
относительная погрешность полученного
результата равна …
1) 0,01 2) 0,06 3) 0.05 (и) 4) 0,02
3. Абсолютная погрешность округления с избытком числа 1,8 до целых равна:
1) -0,2 2) 0,1 3) 0 4) 0,2 (И)
4. Приближённое значение интеграла
![]() ,
вычисленное по формуле прямоугольников
,
вычисленное по формуле прямоугольников
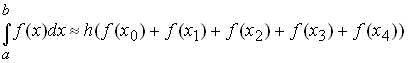
Где
![]() ,
,
![]() ,
,
![]() равно:
равно:
1) 5 2) 10 (и) 3) 15 4) 12,5
5. По таблице функции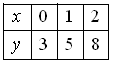 составлена
таблица конечных разностей:
составлена
таблица конечных разностей:
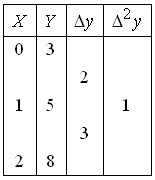
Тогда приближённое значение производной
функции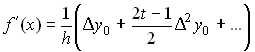 где
где
![]() ,
в точке
,
в точке
![]() ,
равно:
,
равно:
1) 2 (и) 2) 3 3) 1 4) 4
6. . Некоторая функция
задана
в виде таблицы
![]() Если
требуется найти значение производной
данной функции
в некоторой точке,
то можно заменить данную, аналитическая
запись которой неизвестна, некоторой
другой функцией
для
которой
и
найти производную функции
Если
шаг таблицы h (разность между соседними
значениями x) является величиной
постоянной, то можно воспользоваться
формулой
Если
требуется найти значение производной
данной функции
в некоторой точке,
то можно заменить данную, аналитическая
запись которой неизвестна, некоторой
другой функцией
для
которой
и
найти производную функции
Если
шаг таблицы h (разность между соседними
значениями x) является величиной
постоянной, то можно воспользоваться
формулой
![]() где
и
Вычисления
производите с двумя знаками после
запятой. Для заданной в виде таблицы
функции
значение
…
где
и
Вычисления
производите с двумя знаками после
запятой. Для заданной в виде таблицы
функции
значение
…
1) –1,22 2) 0,52 3) 0,60 4) 0,68 (и)
7. Если последовательные значения
функции, являющейся решением задачи
Коши для дифференциального уравнения
![]() с
начальными условиями
с
начальными условиями
![]() ,
,
![]() ,
находятся по методу Эйлера
,
находятся по методу Эйлера
![]() ,
то
,
то
![]() ,
определяемое уравнением
,
определяемое уравнением
![]() ,
при
,
при
![]() и шаге
и шаге
![]() ,
равно:
,
равно:
1) 2 2) 1,1 (и) 3) 1,2 4) 1,3
8. Конечная разность первого порядка
![]() функции
функции
![]() при
начальном значении
при
начальном значении
![]() и шаге
и шаге
![]() равна:
равна:
1) 1 2) 2 (и) 3) 3 4) -2
9. Первое приближение к значению корня
уравнения
![]() ,
расположенного на отрезке
,
расположенного на отрезке
![]() ,
полученное методом хорд по формуле
,
полученное методом хорд по формуле
![]() ,
где а и b –концы отрезка
,
где а и b –концы отрезка
![]() ,
равно:
,
равно:
1) 0,5 2) 0,2 (и) 3) -0,2 4) 0,25
10. Приближенное значение интеграла
 ,
вычисленное по формуле прямоугольников
,
вычисленное по формуле прямоугольников
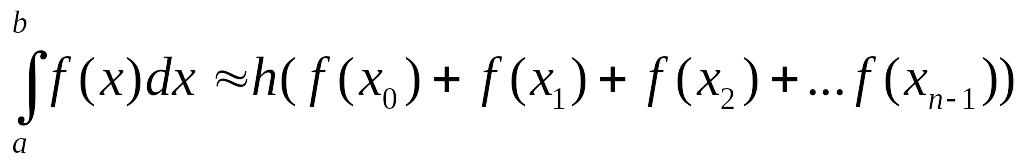 ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
равно:
,
равно:
1) 24 2) 22,5 3) 27 4) 20 (И)
11. Приближенное значение функции
![]() ,
вычисленное с помощью дифференциала,
при
,
вычисленное с помощью дифференциала,
при
![]() равно:
равно:
1) 3,2 2) 0,02 3) 2,98 4) 3,02 (И)
12. Если последовательные значения
функции, определяемой дифференциальным
уравнением
![]() ,
находятся по методу Эйлера
,
находятся по методу Эйлера
![]() ,
то
,
то
![]() ,
определяемое уравнением
,
определяемое уравнением
![]() ,
при
,
при
![]() ,
,
![]() и шаге
и шаге
![]() ,
равно:
,
равно:
1) 6 2) 1,! 3) 5 4) 1,5 (И)
13. Вычислили значение функции
 при
при
![]() и
получили
результат равный 5.
Известны
относительные погрешности чисел 10
и 20:
и
получили
результат равный 5.
Известны
относительные погрешности чисел 10
и 20:
![]() Тогда
относительная погрешность полученного
результата равна …
Тогда
относительная погрешность полученного
результата равна …
1) 0,04 (и) 2)0,03 3) 0,02 4) 0,01
14.Некоторая функция
задана
в виде таблицы
Если
требуется найти значение производной
данной функции
в некоторой точке,
то можно заменить данную, аналитическая
запись которой неизвестна, некоторой
другой функцией
![]() ,
для которой
и
найти производную функции
Если
шаг таблицы h (разность между соседними
значениями x) является величиной
постоянной, то можно воспользоваться
формулой
,
для которой
и
найти производную функции
Если
шаг таблицы h (разность между соседними
значениями x) является величиной
постоянной, то можно воспользоваться
формулой
![]() где
и
Вычисления
производите с двумя знаками после
запятой. Для заданной в виде таблицы
функции
значение
…
где
и
Вычисления
производите с двумя знаками после
запятой. Для заданной в виде таблицы
функции
значение
…
1) -0,36 2)0,64 3) 0,70 4) 0,76 (и)
14. Воспользоваться методом Эйлера:
.
Тогда для уравнения
![]() при
начальном условии
при
начальном условии
![]() с
шагом
h = 0,1 значение
с
точностью до сотых равно …
с
шагом
h = 0,1 значение
с
точностью до сотых равно …
1) 2,90 2) 3,00 (и) 3) 2,40 4) 1,26
15. Для приближенного вычисления
определенного интеграла от функции
![]() на
интервале
можно
воспользоваться формулой
трапеций
Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения
на
интервале
можно
воспользоваться формулой
трапеций
Интервал
разбили
на 4 равные части и вычислили соответствующие
приближенные значения
![]() .
.
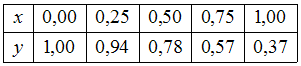 Тогда
Тогда
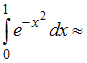 …
…
1) 1,86 2) 0,18 3) 2,08 4) 0,74 (и)
16. При вычислении значения выражения
![]() данные
в условии задачи значения
данные
в условии задачи значения
![]() и
и
![]() округлили
до целых и получили:
округлили
до целых и получили:
![]() Тогда
абсолютная погрешность полученного
результата равна …
Тогда
абсолютная погрешность полученного
результата равна …
1) 1 (и) 2) 0.3 3) 0,2 4) 0,8
17. Для некоторой функции известна таблица ее значений . Тогда конечная разность равна … 1) 0,2 (и) 2)-0,2 3) -0,4 4) 0 18.
Для приближенного решения дифференциального
уравнения
с
начальным условием
можно
воспользоваться методом Эйлера:
.
Тогда
для уравнения
1) 2,80 2) 1,60 3) 4,85 4) 3,61 (и)
19. Известно, что ребра прямоугольного параллелепипеда равны 103 см, 21 см и 98 см. Для упрощения вычислений эти числа округлили до 100 см, 20 см и 100 см соответственно. Нашли объем: (куб. см.) Полученный результат имеет относительную погрешность, равную … 1) 0,01 2) 0,02 3) 0,1 (и) 4) 0,5 20.
Для приближенного вычисления значения
функции y(x) в точке
1)
21.
Для вычисления объема куба было
измерено линейкой его ребро. Оно
оказалось равным 10 см. Известно,
что погрешность измерения линейкой
равна 0,5 см.
Объем куба будет
1) 0,01 2) 0,03 3)0,05 4) 0,15 (и)
|
22. Для приближенного решения
дифференциального уравнения
с
начальным условием
можно
воспользоваться методом Эйлера:
.
Тогда для уравнения
![]() при
начальном условии
с
шагом h = 0,1 и точностью до десятых
равно …
при
начальном условии
с
шагом h = 0,1 и точностью до десятых
равно …
1) 2,19 2) -2,54 3) 2,40 (и) 4) -2,80
23. Некоторая функция
![]() задана
в виде таблицы
задана
в виде таблицы
![]() Если
требуется найти значение производной
данной функции
в некоторой точке то
можно заменить данную, аналитическая
запись которой неизвестна, некоторой
другой функцией
Если
требуется найти значение производной
данной функции
в некоторой точке то
можно заменить данную, аналитическая
запись которой неизвестна, некоторой
другой функцией
![]() для
которой
для
которой
![]() и
найти производную функции
и
найти производную функции
![]() Если
шаг таблицы h (разность между соседними
значениями x) является величиной
постоянной, то можно воспользоваться
формулой
Если
шаг таблицы h (разность между соседними
значениями x) является величиной
постоянной, то можно воспользоваться
формулой
![]() ,
где
и
,
где
и
![]() .
Вычисления производите с двумя знаками
после запятой. Для заданной в виде
таблицы функции
значение
…
.
Вычисления производите с двумя знаками
после запятой. Для заданной в виде
таблицы функции
значение
…
1) -2,22 2) 0,44 (и) 3) 0,76 4) 3.40
24. Для приближенного вычисления определенного интеграла от функции на интервале можно воспользоваться формулой трапеций Интервал разбили на 4 равные части и вычислили соответствующие приближенные значения функции . Получили: , тогда …
0,23 (и) 2) 0,92 3) 0,02 4) 1,04
