Раздел III. Введение в логику. Лекция № 8. Элементы математической логики.

Математическая логика – разновидность формальной логики, т.е. науки, которая изучает умозаключения с точки зрения их формального строения.

Определение. Высказыванием называется предложение, к которому возможно применить понятия истинно или ложно.

В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.

Понятно, что истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами “и”, “или”.

Таким образом, операции с высказываниями можно описывать с помощью некоторого математического аппарата.

Вводятся следующие логические операции (связки) над высказываниями

1. Отрицание. Отрицанием (логическим “не”) высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно.

Обозначается Р или .

Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:

P	Р
И	Л
Л	И

2) Конъюнкция. Конъюнкцией (логическим “и”) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.

Обозначается P&Q или РQ.

P	Q	P&Q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

3) Дизъюнкция. Дизъюнкцией (логическим “или”) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.

Обозначается PQ.

P	Q	PQ
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

4) Импликация. Импликацией (логическим следованием) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно.

Обозначается PQ (или РQ). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.

P	Q	PQ
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

5) Эквиваленция. Эквиваленцией (логической равносильностью) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.

Обозначается РQ или РQ.

P	Q	PQ
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул.

Замечание. В дальнейшем мы познакомимся с принципиально иной, более широкой трактовкой тех понятий, которые мы определили в данной лекции. Мы будем их рассматривать уже не как операции над высказываниями, но как некоторые функции. Поясним на следующем примере. Запись можно рассматривать как обозначение бинарной операции умножения переменных и , а, с другой стороны, так же обозначается функция двух переменных .

Пример 1. С помощью таблиц истинности проверить, являются ли эквивалентными формулы  и .

Составим таблицы истинности для каждой формулы:

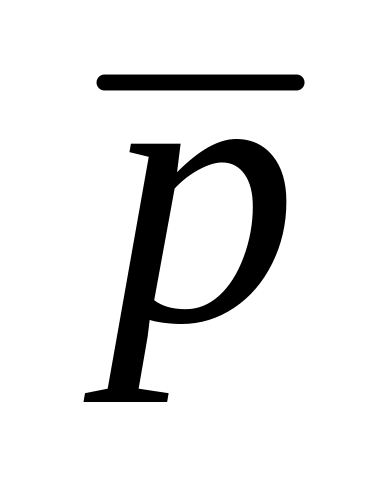
p	r		(pr)
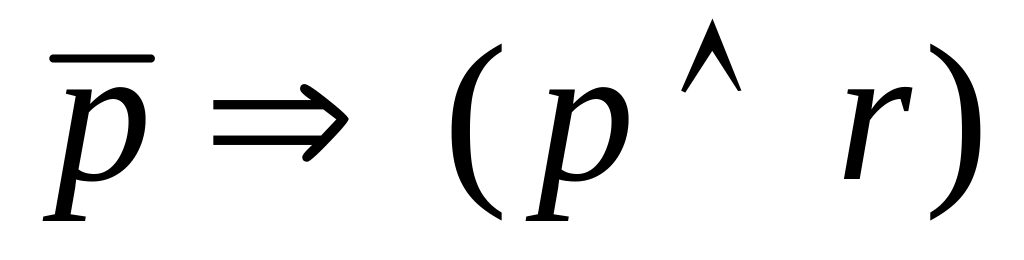
И	И	Л	И	И
И	Л	Л	Л	И
Л	И	И	Л	Л
Л	Л	И	Л	Л

p	r
И	И	Л	Л	Л	И
И	Л	Л	И	И	И
Л	И	И	Л	И	И
Л	Л	И	И	И	И

Данные формулы не являются эквивалентными.

Пример 2. С помощью таблиц истинности проверить, являются ли эквивалентными формулы  и .

Составим таблицы истинности для заданных формул.

p	q	r	pq	(pq)r
И	И	И	И	И
И	И	Л	И	И
И	Л	И	Л	И
И	Л	Л	Л	Л
Л	И	И	Л	И
Л	И	Л	Л	Л
Л	Л	И	И	И
Л	Л	Л	И	И

p	q	r	pq	qp	(pq)(qp)	(pq)(qp)r
И	И	И	И	И	И	И
И	И	Л	И	И	И	И
И	Л	И	Л	И	И	И
И	Л	Л	Л	И	И	И
Л	И	И	И	Л	И	И
Л	И	Л	И	Л	И	И
Л	Л	И	И	И	И	И
Л	Л	Л	И	И	И	И

Из составленных таблиц видно, что данные формулы не равносильны.

Основные равносильности.

Для любых формул А, В и С справедливы следующие равносильности:

A & B  B & A; A & A  A; A & (B & C)  (A & B) & C;

A  B  B  A; A  A  A; A  (B  C)  (A  B)  C;

A  (B & C)  (A  B) & (A  C); A & (B  C)  (A & B)  (A & C);

A & (A  B)  A; A  (A & B)  A; A  A; (A & B)  A  B;

A  (A & B)  (A & B); A  (A  B) & (A  B);