5. Вычисление тройного интеграла по любой области. Пример.

Пусть функция f(x, y, z) определена на ЕR³.

Е_ху – проекция множества Е на плоскость (х, у), если множество Е={(x, y, z)(x, y)E_xy, z₀(x, y)zZ(x, y)}.

E_xy={(x, y)axb, y₀(x)yY(x)},

где функции Z(x, y), y₀(x), Y(x) соответственно непрерывны на [a, b] и на множестве {Е_ху}. f(x, y, z) также непрерывна на {E}. Тогда имеет место формула:

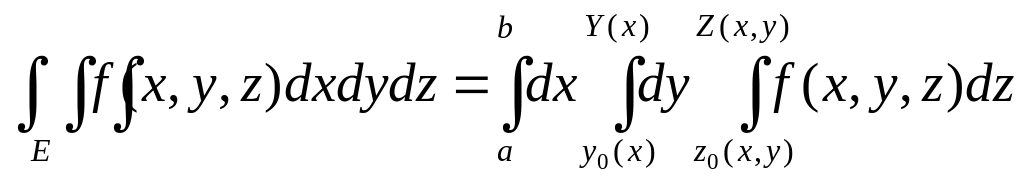
При f(x, y, z)=1 ((x, y, z)E) получим:

6. Геометрический смысл двойного интеграла.

Пусть в R³ задана непрерывная поверхность z=f(x, y)E, где Е – квадрируемая область. Пусть функция f(x, y) интегрируема на Е и не отрицательна. Требуется определить объем тела, ограниченного сверху поверхностью z=f(x, y), снизу плоскостью z=0, с боков цилиндрической поверхностью, проходящей через границу Е_ху, образующая которой параллельна оси Oz.

Разобьем Е_ху на конечное число частей {E_i}. В каждом {E_i} произвольным образом возьмем точку M_i. Посчитаем значение функции в этой точке M_i. Отметим, что каждая {E_i} – квадрируемая фигура и все {E_i} не имеют общих внутренних точек.

Пусть diam (E_i)=sup{(M₁, M₂)M₁E_i, M₂E_i}.

Просуммируем значение функций в М₁, умноженных на меру Е:

Если f(x, y)=1, то:

7. Основные свойства кратных интегралов.

Линейность.

Если функции f и g интегрируемы на Е и R¹, R¹, тогда функция f+g интегрируема на Е:

Адитивность.

Если Е=Е₁Е₂ и {E₁} и {E₂} не имеют общих внутренних точек (₁₂diamE), тогда из интегрируемости функции на Е следует интегрируемость функции на Е₁ и Е₂:

Если f и g интегрируемы на Е и для любых (х, у)Е, ((x, y, z)E), f(x, y)g(x, y) (f(x, y, z) g(x, y, z)), то:

Если функция f интегрируема на Е, то:

Если функция f непрерывна на Е, то существует хотя бы одна точка М(х^*, у^*) (М(x^*, y^*, z^*))такая, что:

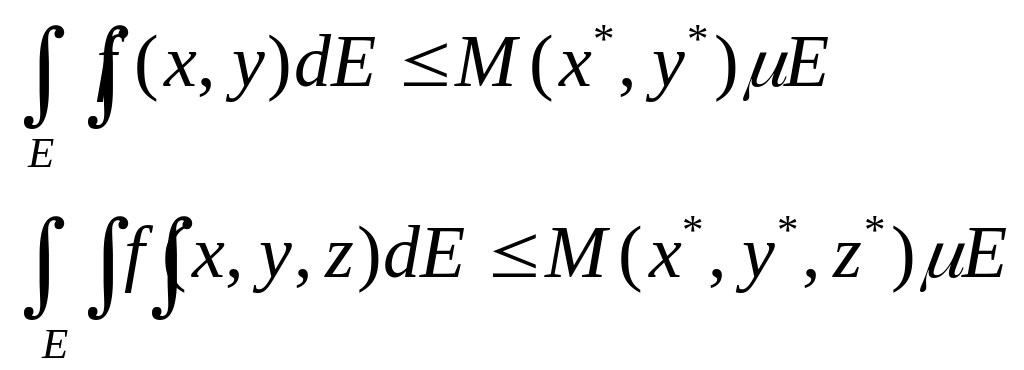
Ограниченность.

Если функция f интегрируема на Е площадь S (объем V), тогда интеграл

ограничен, при чем:

где m и М – соответственно точная нижняя грань и точная верх­няя грань множества значений функции f.

8. Существование кратных интегралов.

Необходимым условием интегрируемости функции f на квадрируемом (кубируемом) множестве Е является ограниченность функции f. Если функция f ограничена на Е, то можно определить нижние и верхние суммы Дарбу.

Определение: Пусть функция f ограничена на квадрируемом (кубируемом) множестве {Е}. Произведем разбиение множества Е на части, которые пересекаются только может быть по своим границам:

Пусть

Тогда нижняя сумма Дарбу:

и верхняя сумма Дарбу функции f:

Свойства сумм Дарбу аналогичны свойствам сумм Дарбу в одномерном случае.

Теорема: Критерий существования……

Для того, чтобы ограниченная на квадрируемом (кубируемом) множестве Е функция f была интегрируемой необходимо и достаточно, чтобы

9. Вычисление двойных двойных интегралов в полярной системе координат. Пример.

Введем прямоугольную систему координат на плоскости ху, у которой положительное направление оси Ох совпадает с направлением полярной оси.

x=cos

y=sin

02

Уравнение  ₁₂ и  непрерывная функция, определяющая в полярной системе координат кривую , т.е. геометрическое место точек, полярные координаты которых удовлетворяют заданному уравнению.

Зададим в плоскости ху область, ограниченную лучами ₁, ₂ и кривой . Пусть в этой области задана непрерывная функция f(x, y). Тогда имеет место равенство:

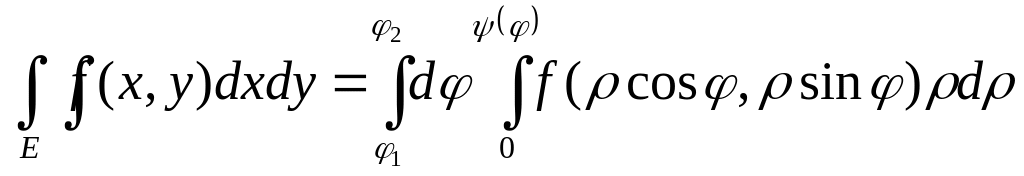Площадь произвольной элементарной фигуры (элемент площади) в полярных координатах равна с точностью до бесконечно малых высшего порядка.

S

dSdd

Строим интегральную сумму:

Пределу при n этой суммы равен двойному интегралу от функции f на Е:

Если центр полярной системы координат расположен внутри границы области Е, то тогда:

В случае если =₁() и =₂(), ₁<<₂ то