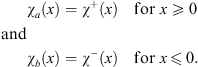- •1. Introduction
- •2. Supersymmetry essentials
- •2.1. A new spacetime symmetry
- •2.2. Supersymmetry and the weak scale
- •2.3. The neutral supersymmetric spectrum
- •2.4. R-Parity
- •2.5. Supersymmetry breaking and dark energy
- •2.6. Minimal supergravity
- •2.7. Summary
- •3. Neutralino cosmology
- •3.1. Freeze out and wimPs
- •3.2. Thermal relic density
- •3.2.1. Bulk region
- •1. Introduction
- •2. Construction of trial functions
- •2.1. A new formulation of perturbative expansion
- •2.2. Trial function for the quantum double-well potential
- •3. Hierarchy theorem and its generalization
- •4. Asymmetric quartic double-well problem
- •4.1. Construction of the first trial function
- •4.2. Construction of the second trial function
- •4.3. Symmetric vs asymmetric potential
- •5. The n-dimensional problem
- •1. Introduction
- •2. The star product formalism
- •3. Geometric algebra and the Clifford star product
- •4. Geometric algebra and classical mechanics
- •5. Non-relativistic quantum mechanics
- •6. Spacetime algebra and Dirac theory
- •7. Conclusions
- •1. Introduction
- •1.1. Historical overview
- •1.2. Aims of this article
- •2. Random curves and lattice models
- •2.1. The Ising and percolation models
- •2.1.1. Exploration process
- •2.2. O (n) model
- •2.3. Potts model
- •2.4. Coulomb gas methods
- •2.4.1. Winding angle distribution
- •2.4.2. N-leg exponent
- •3.1. The postulates of sle
- •3.2. Loewner’s equation
- •3.3. Schramm–Loewner evolution
- •3.4. Simple properties of sle
- •3.4.1. Phases of sle
- •3.4.2. Sle duality
- •3.5. Special values of κ
- •3.5.1. Locality
- •3.5.2. Restriction
- •3.6. Radial sle and the winding angle
- •3.6.1. Identification with lattice models
- •4. Calculating with sle
- •4.1. Schramm’s formula
- •4.2. Crossing probability
- •4.3. Critical exponents from sle
- •4.3.1. The fractal dimension of sle
- •4.3.2. Crossing exponent
- •4.3.3. The one-arm exponent
- •5. Relation to conformal field theory
- •5.1. Basics of cft
- •5.2. Radial quantisation
- •5.3. Curves and states
- •5.4. Differential equations
- •5.4.1. Calogero–Sutherland model
- •6. Related ideas
- •6.1. Multiple slEs
- •6.2. Other variants of sle
- •6.3. Other growth models
- •1. Introduction
- •1.1. Acoustic force field
- •1.2. Primary axial acoustic force
- •1.3. Primary and secondary acoustic force
- •2. Application of Newton’s second law
- •3. Mathematical model
- •3.1. Preliminary analysis
- •4. Equation for particle trajectories
- •5. Concentration equation
- •6. Experimental procedure and results
- •6.1. SiC particle trajectories in an acoustic field
- •7. Comparison between experimental results and mathematical model
- •8. Summary and conclusions
4.3. Symmetric vs asymmetric potential
As we shall discuss, the general description leading from the trial function χ (x) to the final wave function ψ (x) that satisfies the Schroedinger equation (4.2) may be set in a more general framework. Decompose any potential V (x) into two parts
|
|
(4.67) |
Next, extend the functions Va (x) and Vb (x) by defining
|
|
(4.68) |
Thus, both Va (x) and Vb (x) are symmetric potential covering the entire x-axis. Let χa (x) and χb (x) be the ground state wave functions of the Hamiltonians T + Va and T + Vb:
|
(T+Va(x))χa(x)=Eaχa(x) |
(4.69a) |
and
|
(T+Vb(x))χb(x)=Ebχb(x). |
(4.69b) |
The symmetry (4.68) implies that
|
|
(4.70) |
and at x = 0
|
|
(4.71) |
Choose the relative normalization factors of χa and χb, so that at x = 0
|
χa(0)=χb(0). |
(4.72) |
The same trial function (4.9) for the specific quartic potential (4.1) is a special example of
|
|
(4.73) |
with
|
|
(4.74) |
In general, from Figs. (4.69a) and (4.69b) we see that χ (x) satisfies
|
|
(4.75) |
Depending on the relative magnitude of Ea and Eb, we define, in the case of Ea > Eb
|
|
(4.76a) |
and
|
|
(4.77a) |
otherwise, if Eb > Ea, we set
|
|
(4.76b) |
and
|
|
(4.77b) |
Thus, we have either
|
|
(4.78a) |
at all finite x, or
|
|
(4.78b) |
at
all finite x.
A comparison between Figs. (4.9),
(4.10),
(4.11),
(4.12),
(4.13),
(4.14),
(4.15),
(4.16)
and (4.17)
and (4.73)–(4.77a)
shows that w (x)
of (4.14)
and the above
![]() differs
only by a constant.
differs
only by a constant.
As in (4.2), ψ (x) is the ground state wave function that satisfies
|
(T+V(x))ψ(x)=Eψ(x), |
(4.79) |
which can also be written in the same form as (1.14)
|
|
(4.80) |
with
|
|
(4.81) |
Here, unlike (1.32), V (x) can now also be asymmetric. Taking the difference between ψ (x) times (4.75) and χ (x) times (4.80), we derive
|
|
(4.82) |
Introduce
|
ψ(x)=χ(x)f(x), |
(4.83) |
in which f (x) satisfies
|
|
(4.84) |
On account of Figs. (4.82) and (4.83), the same equation can also be written as
|
|
(4.85) |
Eq. (4.80) will again be solved iteratively by introducing
|
ψn(x)=χ(x)fn(x) |
(4.86) |
with
ψn
and its associated energy
![]() determined
by
determined
by
|
|
(4.87) |
and
|
|
(4.88) |
In terms of fn (x), we have
|
|
(4.89) |
On account of (4.88), we also have
|
|
(4.90) |
and
|
|
(4.91) |
For definiteness, let us assume that
|
Ea>Eb |
(4.92) |
in
Figs. (4.69a)
and (4.69b);
therefore
![]() and
and
![]() ,
in accordance with (4.76a).
Start
with, for n = 0,
,
in accordance with (4.76a).
Start
with, for n = 0,
|
f0(x)=1, |
(4.93) |
we can derive {En} and {fn (x)}, with
|
|
(4.94) |
by using the boundary conditions, either
|
|
(4.95) |
or
|
|
(4.96) |
It
is straightforward to generalize the Hierarchy theorem to the present
case. As in Section 3,
in Case (A), the validity of the Hierarchy theorem imposes no
condition on the magnitude of
![]() .
But in Case (B) we assume
.
But in Case (B) we assume
![]() to
be not too large so that (4.91)
and the boundary condition fn (−∞) = 1
is consistent with
to
be not too large so that (4.91)
and the boundary condition fn (−∞) = 1
is consistent with
|
fn(x)>0 |
(4.95) |
for all finite x. From the Hierarchy theorem, we find in Case (A)
|
E1>E2>E3> |
(4.96) |
and
|
1 |
(4.97) |
while in Case (B)
|
E1>E3>E5> |
(4.98) |
|
E2<E4<E6< |
(4.99) |
|
1 |
(4.100) |
and
|
1 |
(4.101) |
A soluble model of an asymmetric square-well potential is given in Appendix A to illustrate these properties.