- •1.Ортогональные и ортонормированные системы функций, ряды Фурье по ортого-
- •§1 Ортогональные системы функций. Ряды Фурье по ортогональным системам функций
- •Частичные суммы рядов Фурье: ядро Дирихле, формулы Дирихле.
- •3.Сходимость ряда Фурье в точке: Принцип локализации, условие Гёльдера, теорема
- •4.Равномерная сходимость ряда Фурье: Неравенство Бесселя, Теорема о равномерной
- •5.Сходимость семейства функций: определение равномерной сходимости семейства
- •6.Собственные интегралы с параметрами: свойства, теорема о дифференцировании
- •§1. Собственные интегралы с параметрами
- •7. Равномерная сходимость несобственного интеграла с параметрами: определение,
- •8. Свойства равномерно сходящихся несобственных интегралов: теоремы о предель-
- •9. Свойства равномерно сходящихся несобственных интегралов: теоремы о диффе-
- •10. Эйлеровы интегралы. Гамма-функция: определение, основное соотношение, про-
- •§3. Эйлеровы интегралы
- •11. Интеграл Фурье: определение, теорема (с леммами) о сходимости интеграла Фу-
- •§4 Интеграл Фурье
- •12. Преобразование Фурье: определение, свойства (ограниченность и непрерывность
- •§5. Преобразования Фурье
- •13. Теоремы о преобразовании Фурье и дифференцировании. Преобразование Фурье
- •14. Системы множеств: определения кольца, минимального кольца. Теорема о сущест-
- •§1 Системы множеств
- •15. Мера клеточных множеств. Теорема о полуаддитивности меры клеточных мно-
- •16. Внешняя мера, измеримые множества, мера Лебега. Свойства внешней меры.
- •17. Теорема о конечной аддитивности меры Лебега. Теорема о счетной аддитивности
- •18. Теорема о непрерывности меры Лебега. Какие множества измеримы по Лебегу?
- •19. Обобщение понятие меры Лебега на случай всей плоскости. Пример неизмеримого
- •20.Мера Лебега-Стилтьеса. Понятие абсолютно-непрерывной, дискретной и сингу-
- •21. Общее понятие меры. Продоление меры. Теорема о существовании и единственно-
- •§3 Общее понятие меры
- •22. Лебегово продолжение меры. Структура системы измеримых по Лебегу множеств.
- •§4. Лебегово продолжение меры
- •23. Измеримые функции: определения (X,y ) – измеримой, -измеримой, борелев-
- •24. Теорема об арифметических операциях с измеримыми функциями. Теорема об из-
- •25.Понятие сходимости почти всюду. Теорема Егорова.
- •26. Понятие сходимости по мере. Две теоремы о связи сходимости по мере и сходимо-
- •27. Простые функции: определение, теорема о простой функции. Необходимое и дос-
- •28. Интеграл Лебега для произвольных функций. Свойства интеграла Лебега. Теорема
- •29. Предельный переход в интеграле Лебега. Теорема Лебега (с док-вом). Теоремы
- •30. Понятие сигма-конечной меры. Интеграл Лебега по множеству бесконечной меры.
- •31. Сравнение интеграла Лебега с интегралом Римана.
- •32. Произведение мер. Формула для нахождения меры множества с помощью интегра-
- •§ 7 Произведение мер. Теорема Фубини.
- •33. Пространства суммируемых функций l1 и l2 . Теорема о полноте пространства l1.
- •§ 8 Пространства суммируемых функций.
4.Равномерная сходимость ряда Фурье: Неравенство Бесселя, Теорема о равномерной
сходимости ряда Фурье.
П.1 Неравенство Бесселя
Теорема.
Пусть
 ,
,
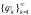 - ортогональна на [a,
b].
Пусть
- ортогональна на [a,
b].
Пусть
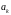 - коэффициенты Фурье. Тогда
- коэффициенты Фурье. Тогда
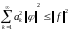
□
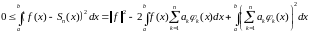 =
=
последнее слагаемое состоит из квадратов и удвоенных попарных произведений, которые равны нулю за счет ортогональности системы
= =
=
Вспомним
формулу:
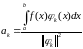
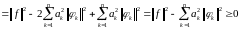 ,
,
следовательно,
частные суммы ограничены:

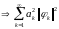 -
сходится.
-
сходится.
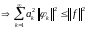 ■
■
Следствия:

 и
и
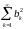 -
сходятся
-
сходятся и
и
 - сходятся
- сходятся
□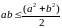 ,
следовательно
,
следовательно
 - ряд сходится. ■
- ряд сходится. ■
П.2 Равномерная сходимость ряда Фурье
Теорема (о равномерной сходимости ряда Фурье)
Пусть
- 2
-периодическая,
непрерывная и кусочно-гладкая на
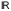 .
.
Тогда ее тригонометрический ряд Фурье сходится к равномерно на .
□
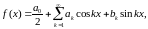

Рассмотрим
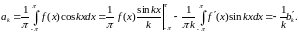
Аналогично
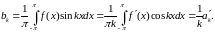

 и
и
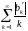 сходятся (по следствию из неравенства
Бесселя)
сходятся (по следствию из неравенства
Бесселя)
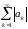 и
и
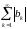 сходятся.
сходятся.
Рассмотрим
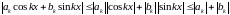
ряд Фурье сходится равномерно к . ■
5.Сходимость семейства функций: определение равномерной сходимости семейства
функций.
6.Собственные интегралы с параметрами: свойства, теорема о дифференцировании
собственного интеграла по параметру, следствие об интеграле с переменными пре-
делами.
§1. Собственные интегралы с параметрами
Пусть
 .
Пусть
.
Пусть
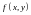 определена на
определена на
 ,
и для
,
и для
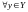
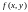 интегрируема по Риману на
интегрируема по Риману на
 ,
то есть
,
то есть
 .
.
Пусть
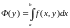 - собственный интеграл с параметром
- собственный интеграл с параметром
 .
.
Пусть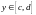 и
- непрерывна на
и
- непрерывна на
 . Тогда
. Тогда
1)
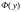 непрерывна на
непрерывна на
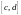 ;
;
2)
если
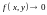 равномерно по
равномерно по
 при
при
 ,
то
,
то 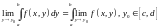 ;
;
3)
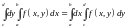 .
.
Теорема
1. Пусть
и
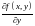 непрерывны в
. Тогда функция
непрерывны в
. Тогда функция
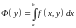 - непрерывно дифференцируема на
и
- непрерывно дифференцируема на
и
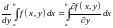 .
.
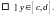
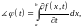


Следовательно,
 ∎
∎
Следствие.

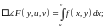
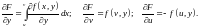
Пусть
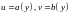 .
Тогда
.
Тогда
 ∎
∎
7. Равномерная сходимость несобственного интеграла с параметрами: определение,
критерий Коши, признаки Вейерштрасса, Дирихле, Абеля.
П.1 Равномерная сходимость
Пусть
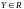 ,
,
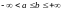 .
Пусть
и
.
Пусть
и
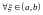
 ,
т.е. точка
,
т.е. точка
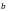 - особая точка несобственного интеграла.
Запишем определение сходящегося
интеграла:
- особая точка несобственного интеграла.
Запишем определение сходящегося
интеграла:
-
сходится при

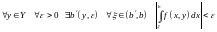
Определение равномерно сходящегося интеграла:
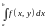 сходится
равномерно (по
)
на
сходится
равномерно (по
)
на

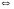
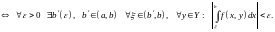
Теорема 1. (Критерий Коши)
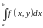 сходится
равномерно на
сходится
равномерно на
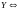

 Необходимость.
Необходимость.
Пусть
сходится равномерно на
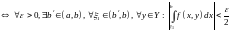 и
и
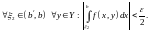 Тогда
Тогда

Достаточность.
Пусть
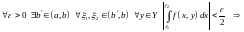
 сходится
при
если
сходится
при
если
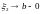 тогда
тогда
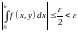 ∎
∎
П. 2. Признаки равномерной сходимости
Теорема 2. (Признак Вейерштрасса)
Пусть
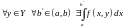 .
Пусть
.
Пусть
 определена на
определена на
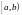 такая, что
такая, что
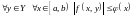 и
и
 сходится. Тогда
сходится равномерно на
.
сходится. Тогда
сходится равномерно на
.
 Так
как
- сходится
Так
как
- сходится

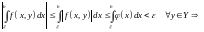
 -
сходится равномерно ∎
-
сходится равномерно ∎
Теорема 3. (Признак Дирихле)
Пусть:
1)
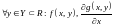 непрерывны по
на
непрерывны по
на
 ;
;
2)
 - первообразная по
- первообразная по
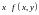 и для
и для
 (первообразные
равномерно ограничены);
(первообразные
равномерно ограничены);
3)
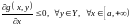 ;
;
4)
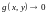 равномерно
на
при
равномерно
на
при
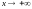 .
.
Тогда
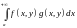 сходится равномерно на
.
сходится равномерно на
.
Так
как
 равномерно
равномерно
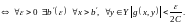

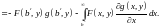
Так как
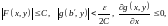
то

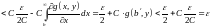 ∎
∎
Признак Абеля
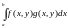 сходится
равномерно
на
,
если:
сходится
равномерно
на
,
если:
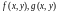 непрерывны
на
непрерывны
на
 ;
;
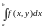 сходится
равномерно на
;
сходится
равномерно на
;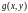 монотонна
по
монотонна
по
 для
для
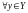 ;
;
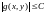 для
для
 ,
.
,
.