I неравенство Чебышева

Пусть X - неотрицательная СВ, имеющая конечное математическое ожидание М(Х), тогда имеет место неравенство вида: 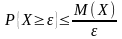, для любого ε > 0.

Т.е. вероятность того, что СВ Х, не меньше ε, не превосходит её математическое ожидание, делённое на ε.

Доказательство:

Введём Y_ε – СВ - индикатор события X ≥ ε

Y_ε = 1 – при X ≥ ε

Y_ε = 0 – при 0 ≤ X ≤ ε

Составим закон распределения СВ Y_ε:

Yε	0	1
Pi	P1	P2

Тогда в силу неотрицательности СВ Х: 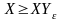и для события X ≥ ε можно заменить Х на ε: . Это неравенство сохранится, если мы применим к нему математическое ожидание:

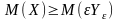
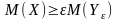заменяем M(Yε) на вероятность:

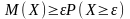
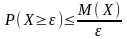ч.т.д.

II неравенство Чебышева

Пусть СВ Х имеет M(X) и D(X). Тогда второе неравенство Чебышева показывает, что вероятность того, что отклонение СВ Х от своего математического ожидания не превосходит дисперсию деленную на ε²:

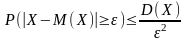
Доказательство: Рассмотрим неравенство 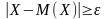, так как обе стороны неравенства положительные возведем в квадрат: . Т.к. эти события равносильны, то и вероятности их равны:

К последнему применим I неравенство Чебышева:

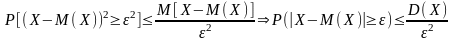ч.т.д.

Другой вид II неравенства Чебышёва:

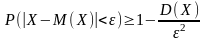
§ Сходимость по вероятности

Ч

О

исло а называется пределом по вероятности для СВ Х_n, зависящей от порядкового номера n, если для любого сколь угодно малого положительного числа ε выполняется неравенство:

Другая запись:

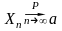
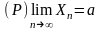
Из этого равенства следует, что СВ X_n примерно равна а, и это выполняется с любой наперёд заданной точностью и надёжностью.

Предел по вероятности отличается от обычного предела последовательности:

1. Для обычного предела {X_n}:

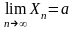: для любого ε > 0 существует такое N = N(ε): такое что как только n>N, будет выполняться неравенство: |X_n - a| < ε.

2. В случае предела по вероятности:

: неравенство |X_n - a| < ε может не выполняться для отдельных значений n; этот предел обладает менее жёсткими требованиями.

§ Закон больших чисел в форме теоремы Чебышева

Под Законом Больших Чисел понимается группа теорем (теоремы Чебышёва, Бернулли, Хинчина и др.); эти теоремы устанавливают условия устойчивости поведения среднего арифметического последовательности случайных величин.

Случайные отклонения от среднего – неизбежные в каждом отдельном явлении, а в массе они взаимно погашаются.

При достаточно большом n среднее арифметическое последовательностей утрачивает случайность и начинает вести себя практически как неслучайная величина, что позволяет предсказывать результаты массовых случайных явлений почти с полной определённостью.

Т

Т

еорема Чебышева

Пусть имеется бесконечная последовательность СВ X₁,X₂,...,X_n , которые:

1. Попарно независимы

2. Имеют различные математические ограничения М(X₁), М(X₂)… М(X_n)

3. Дисперсия каждой из величин не превосходит постоянного числа С:

D(Х_i) ≤ С

Тогда среднее арифметическое первых n случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:

Доказательство: Введём событие 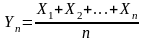, тогда

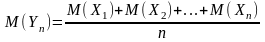
Согласно II неравенству Чебышева будет выполнятся след условие:

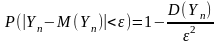, для ε > 0 (*)

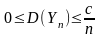В пределе:

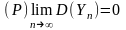
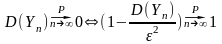
Возьмем придел по вероятности выражения (*):

Таким образом

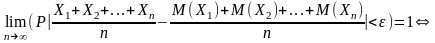
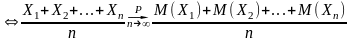
Следствие: Предположим, что все математические ожидания равны:

М(Х_i) = а при i=1,2,..., n, тогда:

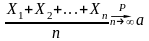
Получяется, что среднее арифметическое при n стремящимся к бесконечности практически становится конечным числом.

§ Сущность Теоремы Чебышева

Хотя отдельные независимые СВ могут принимать значения далёкие от их математического ожидания, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значение близкое к постоянному числу:

Поведение каждой из случайных величин и их среднего арифметического отличаются; нельзя заранее предсказать, какое из значений примет случайная величина, но можно предсказать, какое из значений примет среднее арифметическое всех случайных величин.

§ Значение Теоремы Чебышёва для практики

Обычно для измерения некоторой постоянной физической величины производят несколько измерений, а после – находят их среднее арифметическое, которое и принимают за искомое значение. Следствие из теоремы Чебышёва даёт обоснование правильности такого способа измерения, а также указывает на условия, при которых он может быть применен. На теореме Чебышёва основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов.

§ Теорема Бернулли

Е

Т

сли производится бесконечная последовательность испытаний по схеме Бернулли относительно некоторого события А (события попарно независимы, а вероятность наступления события А равна р), то вероятность отклонения относительной частоты от вероятности р наступления события А будет сколь угодно малой, если число испытаний n неограниченно возрастает: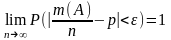

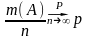, где 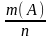- относительная частота события А

Доказательство: Обозначим через Х - ДСВ, которая есть число появлений события А в n испытаний. Через J_k обозначим число появления события А в k-том испытании, – это индикатор события А. Тогда:

Составим закон распределения для индикатора:

Jk	0	1
P	q	p

q = 1- р

Запишем:

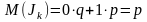
Применим теорему Чебышева для первых n членов:

ч.т.д.

Сущность теоремы Бернулли

1 . Теорема Бернулли объясняет, почему относительная частота событий при n ∞ обладает свойством устойчивости.

2. Теорема Бернулли оправдывает статистическое определение вероятности.

Лекция 13

§ Понятие о центральной предельной теореме (ЦПТ)

Д

О

ругая группа предельных теорем, устанавливающая сходимость законов распределения для последовательности сумм случайных величин (в виде ее особой важности как для теории, так и для приложений), носит название Центральной предельной теоремы.

С одной из этих теорем мы уже знакомы – это теорема Муавра-Лапласа. Она является лишь частный случай ЦПТ.

В ЦПТ исследуется вопрос возникновения нормального распределения как предельного для суммы случайных величин, имеющих различные законы распределения с увеличением числа слагаемых. Эта проблема в общей форме была поставлена в исследованиях Чебышева, а его ученик Ляпунов в 1901 году получил весьма общие достаточные условия, и поэтому теорема носит его имя. В 1922 году финский математик Линдеберг получил достаточные условия, оказавшиеся затем и необходимыми – это выяснил американский математик Феллер в 1935 году.

Приведем формулировку ЦПТ в случае, когда слагаемые распределены одинаково – это Теорема Леви.

Теорема Леви

С

О

В X является центрированной и нормированной, если ее математическое ожидание равно нулю, а ее дисперсия равна единице.

Можно показать, что любая СВ с конечной дисперсией σ² и M(X)=а можно центрировать и нормировать с помощью следующих действий:

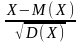- центрированная и нормированная случайная величина.

При и

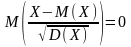
Для суммы случайных величин S_n = X₁ + X₂ +…+ X_n, при , ,

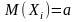составим центрированную и нормированную величину Y_n :

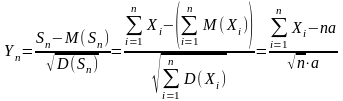
Т

Т

еорема Леви (ЦПТ в случае одинаково распределенных случайных величин):

1. Пусть СВ X₁, X₂, …, X_n – взаимно независимы и одинаково распределены;

2. , при i = 1,2, …, n

3. 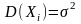, при i = 1,2, …, n

Тогда функция распределения центрированной и нормированной суммы этих случайных величин для Y_n, при n → ∞ – стремится к функции распределения нормальной СВ с параметрами (0;1). Т.е. для любого фиксированного Х функция распределения Y_n будет стремится к следующему нормальному закону распределения случайной величины:

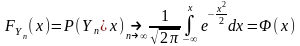- Функция Лапласа

Нормальный закон распределения широко применяется во всех явлениях:

• ошибка измерения распределена нормально, т.к. является суммой большого числа малых ошибок, происходящих из-за колебания параметров среды измерения, а также колебаний состояния субъекта и объекта измерения;

• нормально распределены координаты точек падения снарядов

• нормально распределена шумовая помеха, возникающая внутри радиотехнических устройств.