Принцип математической индукции

Пусть Р(п) – предикат, определенный для всех натуральных чисел n.

Предположим, что

1. Р(1) истинно и

2. k≥ 1 импликация (Р(k) Р(k+1)) верна.

Тогда Р(п) истинно при любом натуральном значении n.

Пример 2.13. Докажите методом математической индукции, что равенство

справедливо при всех натуральных п.

Решение. Пусть Р(п) – предикат

В случае п=1 левая и правая части равенства равны 1.

Следовательно, Р(1) истинно.

Предположим теперь, что равенство имеет место для какого-то натурального числа k. Тогда

Таким образом, при любом натуральном kимпликация

Р(k) P(k+1)

справедлива. Значит, по принципу математической индукции, предикат Р(п) имеет истинное значение при всех натуральных п.

Пример 2.14. Методом математической индукции докажите, что 7ⁿ–1 делится на 6 при любом натуральном показателе п.Решение. Целое числоа делится на целое число bтогда и только тогда, когда выполняется равенство а=mbпри каком-то целом числе т. Например, 51 делится на 17, поскольку 51=3×17. Кроме того, известно простое свойство делимости чисел, которое утверждает, что сумма делящихся на bчисел также делится на b.

Пусть Р(п)обозначает предикат «7ⁿ–1 делится на 6».

При п=1 имеем 7ⁿ–1=7–1=6, т.е. предикат Р(1) имеет истинное значение.

Предположим, что 7^k–1 делится на 6 при каком-то натуральном k. Тогда

7^k+1–1= 7(7^k–1)+7–1 = 7(7^k–1)+6.

Так как 7^k–1 делится на 6, то по упомянутому свойству делимости сумма 7(7^k–1)+6 тоже делится на 6.

Итак, 7^k+1–1 делится на 6, так что при любом натуральном kимпликация (Р(k) Р(k+1)) истинна.

Индуктивным рассуждением мы доказали истинность предиката Р(п) для всех натуральных п.

№8

Чтобы доказать корректность алгоритма нужно проверить все изменения используемых в нем переменных до, в течение и после работы алгоритма.

Пусть Р – предикат, истинный для входных данных алгоритмаА, и Q– предикат, описывающий условия, которым должны удовлетворять выходные данные. Высказывание {Р}A{Q}означает, что «если работа алгоритма А начинается с истинного значения предиката Р, то она закончится при истинном значении Q». Предикат Рназывается входным условием или предусловием, aQ– выходным условием или постусловием. Высказывание {Р}A{Q}само является предикатом. Поэтому доказательство корректности алгоритма А равносильно доказательству истинности {Р}A{Q}.

Задача 1. Докажите корректность алгоритма Разность.

Разность

begin

z:=x–y;

end

Решение. В данном случае предусловием Рявляются равенства: х=х₁и y=y₁. Постусловие Q– это z=x₁–y₁. Предикат {Р} Разность {Q} читается как «если х=х₁и у=у₁, то z=х₁–y₁». Истинность последнего предиката легко проверяется подстановкой х=х₁и у=у₁ в тело алгоритма, содержащего переменные z, xи у. С формальной точки зрения соотношения: z=х–у, х=х₁и у=у₁влекут тождество z = х₁–y₁.

Когда в алгоритмеАпроисходит много различных действий с переменными, мы разбиваем его на подходящие отрезки А₁, A₂, ..., А_п и доказываем цепочку утверждений вида

{P}A₁{Q₁}, {Q₁}A₂{Q₂}, ...,{Q_n-1}A_n{Q_n},

где постусловие любого отрезка служит предусловием следующего.

Задача 2 Докажите методом математической индукции корректность алгоритма Квадрат.

Квадрат

{n – натуральное число}

begin

sq:=0;

for i:= 1 to ndo

sq:=sq+2i–1;

end

{sq= n²}

Решение. Пусть Р(п)обозначает предикат «sq=n²после n-го прохода цикла», asq_k– значение переменной sqпосле k;-го прохода цикла. Покажем, что

(1) sq₁= 1²;

(2) если sq_k= k², то sq_k+i = (k+1)².

Очевидно, что после первого прохода цикла sq₁= 1 и пункт (1) выполнен. Предположим, что после k-ой петли цикла sq_k= k². Тогда после следующего прохода

sq_k+1= sq_k+ 2(k+1)–1 = k²+2k+1 = (k+1)².

Таким образом, пункт (2) тоже выполняется.

Итак, мы установили, что Р(1) истинно. Кроме того, по второму пункту импликация (Р(k)Р(k+1)) справедлива при любом k≥1. Следовательно, согласно принципу математической индукции, Р(п) истинно для всех натуральных п.

№9

Множество – это совокупность объектов, называемых элементами множества. Например,

• {Брест, Витебск, Гомель, Гродно, Минск, Могилев};

• {2, 3, 5, 7, 11};

• {сыр, яйцо, молоко, сметана}

В общем случае записьаSозначает, что объект а является элементом множества S. Часто говорят, чтоа принадлежит множеству S. Если объекта не принадлежит S, то пишут: аS.

Мы не можем выписать все элементы очень больших, в особенности бесконечных множеств. В этом случае множества определяются с помощью подходящих предикатов. Формально мы пишем

S = {х: Р(х)}

для описания множества, состоящего из элементов х, для которых предикат Р(х)имеет истинное значение. Например, запись

S = {х: х – нечетное натуральное число}

описывает множество S = {1, 3, 5, 7, ...}.

1) множествоАявляется подмножествоммножества S, если каждый его элемент является элементом множества S. Говорят, что множествоА содержится в множестве S. Этот факт обозначают так: АS. На рис. 3.1 дана диаграмма Венна, которая иллюстрирует это определение.

2)Два множества считаются равными, если каждое из них содержится в другом. Поэтому для доказательства равенства множеств нам нужно показать, что они состоят из одних и тех же элементов. На формальном языке для равенства множествА=В необходимо проверить истинность двух импликаций:

{хА хВ} и {хВ  хА}.

Рисуно4. Диаграмма Венна подмножестваАS

Пример 3.2. Пусть

А = {п: п²– нечетное целое число},

В = {п: п – нечетное целое число}.

Показать, чтоА= В.

Решение. Если хА, то х²– нечетное целое число, что было доказано в примере 2.11. Отсюда вытекает, что само число х – целое и нечетное. Следовательно, хВ, т.е. АВ.

С другой стороны, пусть хВ. Тогда х – нечетное целое число. Согласно примеру 2.10, в этом случае х²тоже будет нечетным целым числом, а значит, хА. В виду произвольности взятого элемента хВ мы можем утверждать, что все элементы из В принадлежат А, т.е. ВА. Итак, А = В.

1.Объединениемдвух множествАи В называется множество

АВ = {х: хАили хВ}.

Оно состоит из тех элементов, которые принадлежат либо множествуА, либо множеству В, а возможно и обоим сразу. Диаграмма Венна объединения двух множеств показана на рис. 3.2.

Рисунок ..5. Диаграмма Венна объединенияАB

2.Пересечениемдвух множеств A и Вназывается множество

АВ = {х:хАихВ}.

Оно состоит из элементов, которые принадлежат как множествуА, так и множеству В. Диаграмма Венна пересечения двух множеств приведена на рис.3.3.

Рисунок ..6. Диаграмма Венна пересеченияАB

3.ДополнениеммножестваВдо множества А или разностью множеств А и Вназывается

А\В = {х: xAиxB}.

ДополнениеА\В состоит из всех элементов множества А, которые не принадлежат В (см. рис. 3.4).

Рисунок.7. Диаграмма Венна разностиА\B

4.Симметрической разностьюдвух множествАи В называют множество

AB = {x: (xA и xB) или (xB и xA)

Оно состоит из всех тех и только тех элементов универсального множества, которые либо принадлежат A и не принадлежатВ, либо наоборот, принадлежат В, но не А. Грубо говоря, симметрическая разность состоит из элементов, лежащих либо в А, либо в В, но не одновременно в обоих множествах. Диаграмма Венна, иллюстрирующая симметрическую разность, нарисована на рис. 3.6.

Рисунок.8. Диаграмма Венна симметрической разности AB

№10

Операции над множествами:

Таблица ..8

Операции над множествами	Логические операции
^­	не
	или
	и
	

Пример 3.5. Докажем, что сделанное в предыдущем примере предположение справедливодля любых множествАи В.

Решение.

= {x : x(AB)} = = {x : не(x(AB))} = = {x : не((xA) и (xB))};

= {x : (xA) или (xB)} = = {x : (не (xA)) или (не (xB))}.

Сравнивая таблицы истинности, легко установить логическую эквивалентность составных предикатов не (Ри Q) и (не Р)или (не Q), где Р и Q– простые высказывания (табл.3.2.).

Таблица ..9

P	Q	P и Q	не (P и Q)	не P	не Q	(не Р)или (не Q)
И	И	И	Л	Л	Л	Л
И	Л	Л	И	Л	И	И
Л	И	Л	И	И	Л	И
Л	Л	Л	И	И	И	И

Опираясь теперь на соответствие между логическими операциями и операциями над множествами (табл. 3.1), можно увидеть, что предикат не (Р и Q) соответствует множеству , а (не Р) или (не Q) – множеству . Следовательно, .

законом двойственности, замена на,  на Uи наоборот.

Таблица.10. Законы алгебры множеств

Законы ассоциативности
A(ВС) = (AВ)С	А(ВС) = (АВ)С
Законы коммутативности
AB= BA	АВ = ВА
Законы тождества
A = A AU = U	AU = A А = 
Законы идемпотентности
АА = А	АА = А
Законы дистрибутивности
А(ВС) = (АВ)(АС)	A(ВС) = (AВ)(AС)
Законы дополнения
A = U =  = A	A =  = U (дополнение пустого множества) = A
Законы де Моргана

Пример 3.7. Уравнение ( B)(A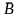 C) = . Определить взаимные включения множеств A, B и C.

Решение. Очевидно, что B=  и A C= . Следовательно, BA. A C = (AC)  =  (AC) B.

Т .к. BA, то CB.Итак, диагирамма Венна взаимного включения множеств A, B и Cимеет вид:

Мощностью конечного множества Sназывается число его элементов. Она обозначается символом |S|.