24. Типы точек покоя. Узел, седло.

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

Характеристическое уравнение этой системы имеет вид:

 Рассмотрим следующие возможные случаи:

1) Корни характеристического уравнения действительные, отрицательные и различные.

Точка покоя  будет устойчива. Такая точка покоя называется устойчивым узлом.

2) Корни характеристического уравнения действительны и

 или .

В этом случае точка покоя также будет устойчива.

3) Хотя бы один из корней  положителен.

В этом случае точка покоя неустойчива, и такую точку называют неустойчивым седлом.

4) Оба корня характеристического уравнения положительны .

В этом случае точка покоя неустойчива, и такую точку называют неустойчивым узлом.

Если полученного решения 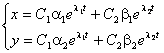системы исключить параметр t, то полученная функция  дает траекторию движения в системе координат XOY.

Возможны следующие случаи:

 

   Устойчивый узел. Неустойчивый узел. Седло.

27. Типы точек покоя. Фокус, центр.

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

Х арактеристическое уравнение этой системы имеет вид:

 Рассмотрим следующие возможные случаи:

5) Корни характеристического уравнения комплексные .

Если р = 0, т.е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.

Такая точка покоя называется центром.

Если  p< 0, то точка покоя устойчива и называется устойчивым фокусом.

Если p > 0, то точка покоя неустойчива и называется неустойчивым фокусом.

29. Линейные и квазилинейные дифференциальные уравнения в частных производных первого порядка.

30. Задача Коши для дифференциальных уравнений в частных производных первого порядка.

31. Системы дифференциальных уравнений в частных производных первого порядка.Системы дифференциальных уравнений первого порядка

1.Пусть f - функция, определенная на некотором множестве GRⁿ⁺²,  -функция, определенная на интервале M R. Тогда  - решение дифференциального уравнения:

f(x,y,y ,y ,...,y⁽ⁿ⁾)=0, (1)

если (общее решение системы (1) содержит n произвольных постоянных c_i, i=1,...,n):

а)  - дифференцируема n раз,

б) x₀M: {(x₀,y₀,y₁,...,y_n): x₀M, y_i=⁽ⁱ⁾(x₀), 0in}G

в) f(x, (x),(x), (x),...,⁽ⁿ⁾(x)) 0 xM.

При этом (1) называют дифференциальным уравнением n-го порядка (не разрешенным относительно старшей производной, заданным в неявном виде). Дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной:

y⁽ⁿ⁾=g(x,y,y,...,y^(n-1)), (2)

где g: Rⁿ⁺¹R. (Пример уравнения, которое нельзя разрешить: (y)²+x=0)

2.Система дифференциальных уравнений 1-го порядка, разрешенный относительно производной:

y₁'=f₁(x,y₁,y₂,...,y_n), y₂'=f₂(x,y₁,y₂,...,y_n),|  y_n'=f_n(x,y₁,y₂,...,y_n),

где f_i: Rⁿ⁺¹R, i=1,...,n.

Аналогично определяется система уравнений высшего порядка, в том числе, не разрешенных относительно старшей производной, например:

J₁(x,y,y',y''y⁽ⁿ⁾,z,z',...,z^(m))=0,  J₂(x,y,y',y'' ,...,y⁽ⁿ⁾,z,z',...,z^(m))=0.

Решением системы (3) называется система функций {₁(x), ₂(x),...,_n(x)}, определенных и дифференцируемых на MR, таких, что xM (x,₁(x),₂(x),...,_n(x))G и _i (x)=f_i(x,₁(x),...,_n(x)), i=1,...,n. Общее решение (3) зависит от постоянных c_i.

3.Пусть MR^m, G Rⁿ⁺², тогда уравнение

F(x,y,y/x₁, y/ x₂,..., y/x_m, ²y/ x₁x₂,..., ⁿy/ x_mⁿ)=0

называется уравнением в частных производных. Например, уравнение Лапласа:

 y= ²y/x₁²+₂y/x₂²=0Здесь решение ищется в области B R² (y=(x₁,x₂)). Можно ставить граничную задачу: определить функцию, гладкую в B и совпадающую с известной функцией g, заданной на границе  B, - это задача Дирихле. Для уравнения Лапласа эта задача разрешима единственным образом.Для уравнений в частных производных так же можно определить систему дифференциальных уравнений.4.Дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной (2), может быть сведено к системе уравнений 1-го порядка: действительно, пусть есть уравнение y⁽ⁿ⁾=g(x,y,y ,y ,...,y^(n-1)).Введем новые обозначения: x₁=y, x₂=y x₃=y ,...,x_n=y^(n-1),тогдаx₁'=x₂,x₂'=x₃,x_n-1'=x_n,  x_n'=g(x,x₁,x₂,...,x_n).Таким образом, уравнение (2) эквивалентно системе(5) в том смысле, что, если  (x) - решение (2), то система функций  _i(x)=^(i-1) (i=1,...,n) будет решением (5) и наоборот, если система  (x) - решение (5), то  ₁(x)= (x) будет решением (2). Это очевидно из замены (4) с последующей подстановкой в систему (2) или (5) соответственно.