24. Числовые характеристики значений св

Для описания СВ как провило дают две ее характиристеки математическое ожидание M(θ) и дисперсию D(θ).

M(θ) - среднее значение, вокруг которого разбросаны допустимые значения СВ

D(θ) - степень разбросанности допустимых значений СВ относительно M(θ).

Она характеризуется математическим ожиданием квадрата

D(θ)=M(θ-М(θ)) = M(θ )-М(θ)

Для бесконечной непрерывной СВ математическое ожидание:

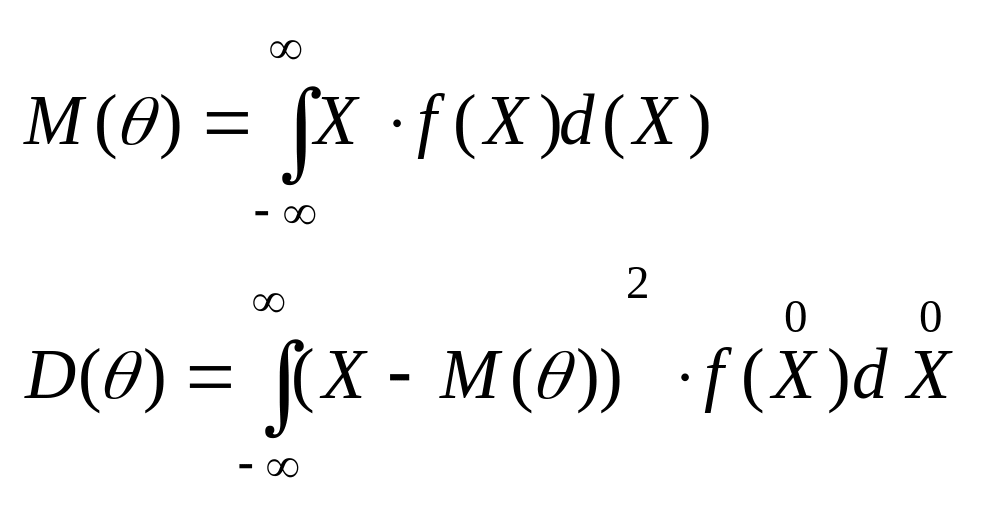
25. Закон распределения непрерывных св. Закон нормального распределения

С помощью функции распределения и плотности распределения можно найти вероятность того, что СВ будет .<= данному допустимому значению или = Р₁

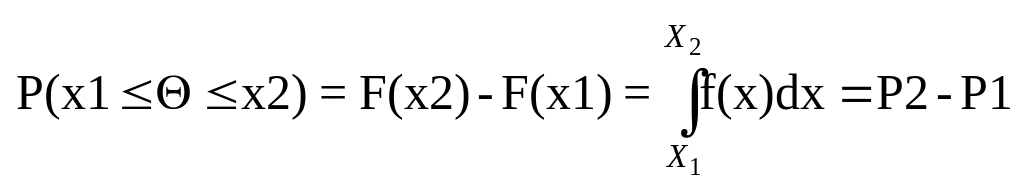
Для этого необходимо знать закон распределения СВ ,т.е функцию и плотность распределения

Закон нормального распределения –открыт в 1733 г. Муавром ,а затем развит и протабулирован Гауссом и Лапласом (1)

плотность нормального распределения

F(x)= (2)

Функция нор100мального распределения -стандарт

a=M(θ),зная (1) и (2) можно найти вероятность неравенства

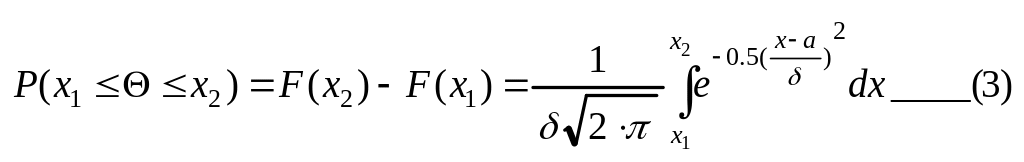Данный интеграл можно протабулировать ,но и такие таблицы нужны для конкретных и а, если а=0 , =1 то этих трудностей можно избежать

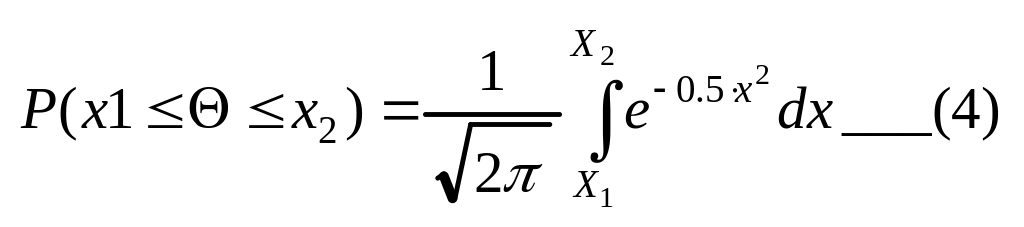
Формулы (1) и (2) примут следующий вид

(5)

функция распределения с а=0 , =1 называется стандартом нормального распределения

переход от нормального к стандартному можно представить графически

Стандартное нормальное распределение для нормированной СВ

, , ;

1).F(x) при а<>0,

2).F₀( ) при а=0 , для

интеграл (функция ) распределения Лапласа

функцию Лапласа можно протабулировать в пределах

В технической литературе существует таблица стандартного нормального распределения и таблицы распределения интегралов Лапласа

Таблица интегралов Лапласа

x	Ф(X)		x	Ф(X)
0.5	0.1915		1.75	0.4599
1.0	0.3413		1.96	0.475
1.28	0.3997		2.51	0.4938
1.34	0.4099		2.58	0.4951
1.64	0.4495		2.75	0.497

Свойства нормального распределения.

1. Выражение вероятности попадания нормированной случайной величины _а=0, =1в любой заданный интервал через функцию Лапласа

P(X`<sub>1</sub> <sub></sub> X`₂)=F₀(X`<sub>2</sub>)- F<sub>0</sub>(X`₁)=Ф(X`<sub>2</sub>)+0.5- Ф(X`₁)-0.5= Ф(X`<sub>2</sub>)- Ф(X`₁)

2. Выражение вероятности попадания случайной величины 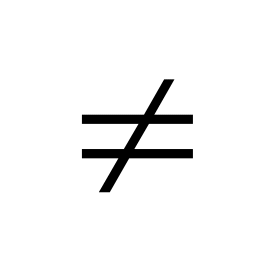а 0,  1в любой заданный интервал через функцию Лапласа

P(X₁  X₂)=F₀(X₂)- F₀(X₁)=P(X`<sub>1</sub> (<sub>0</sub>а) X`₂)=

P( ₀ )=Ф( )-Ф( )

Для вероятности того, что случайная величина не превысит заданные значения 1-е и 2-е свойства имеют следующий вид.

1`) P(<sub>0</sub> X`₁)=Ф(X₁)+0.5

2`) P( X₁)=Ф( )+0.5

3-е и 4-е свойства рассмотрим при симметричном распределении случайной величины относительно математического ожидания

P(X₁  X₂)=P(a-  a+)= P(- -a )= P(-  ).

=-a=-M() – абсолютное отклонение.

Сформулируем задачу об абсолютном отклонении. Найти вероятность того, что абсолютное отклонение не превысит некоторого заданного числа.

  заданное число.

P( )= P(-  ) P(- (-a ) )= P(a-  a+)= P(a- ₀а a+)= P(- ₀ )= P(- ₀ )= Ф()- Ф(-)=Ф()+ Ф()=2 Ф().

Таким образом, сформулируем третье свойство нормального распределения. Выражение вероятности того, что абсолютное отклонение не превысит заданного числа через функцию Лапласа этого числа и стандарт

3. P( )=2 Ф()

P( )=2 Ф(), т.к. 

Заданное число можно выразить через стандарт t.

4. P( )=2 Ф()=2 Ф((t))=2 Ф(t)

P(₀ )=2 Ф()=2 Ф(t), т.к. 

Вероятность того, что абсолютное отклонение нормального распределения случайной величины не превысит некоторого предела зависит только от того во сколько раз t превышает стандарт 

P( )=P(₀ )=2 Ф(t)

Происхождение названия стандарт для исходит из-за того, что с этой величиной сравнивают все отклонения.