1. Процедура оценки параметров по методу наименьших квадратов. В “классическом” варианте мнк в отношении свойств ошибки модели t выдвигаются следующие предположения:

– ошибка имеет нулевое математическое ожидание, M[_t]=0;

– ее дисперсия конечна и постоянна, _²=const;

– автокорреляционные связи в ряду ошибки отсутствуют, т. е. ₁=₂=...=0, где _i – коэффициент автокорреляции рядов _t и _t–i, i=1,2,... ;

– Ряд значений ошибки статистически не связан с рядами значений независимых переменных модели [5, с.358].

Рассмотренные предположения определяют ошибку модели как процесс белого шума с ковариационной матрицей ее вектора ошибки, имеющей следующий вид: Cov()=_²Е.

Рассмотрим общую схему процедуру оценки параметров линейной эконометрической модели на основе МНК более подробно. Такая модель в общем виде представлена уравнением (1):

y_t=₀+₁ х_1t +...+_nх_nt +_t. (1)

Исходными данными при оценке параметров ₀, ₁,..., _n являются измеренные (наблюдаемые) значения зависимой переменной, которые можно представить в виде вектора-столбца,

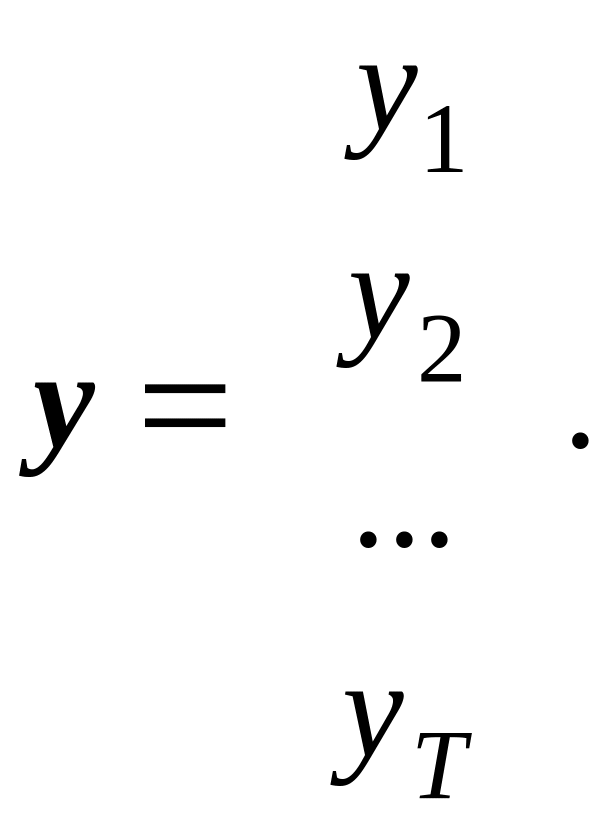
Н аблюдаемые значения независимых переменных объединим в матрицу следующего вида:

Х =

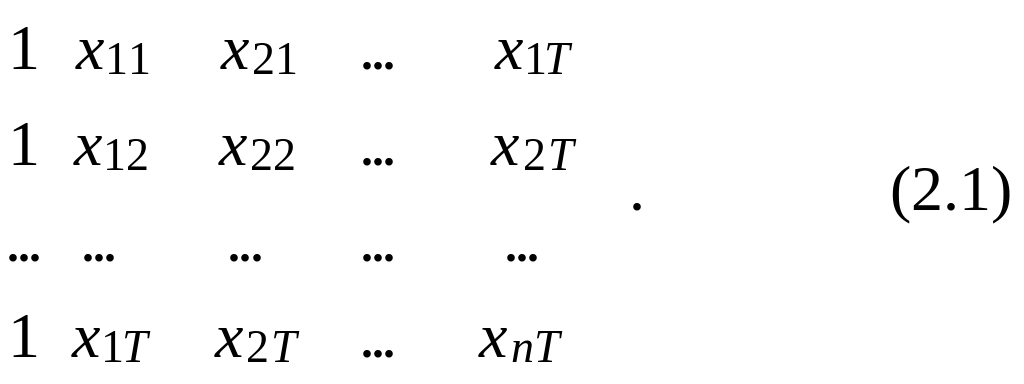
Cвое название МНК получил, исходя из смыслового содержания критерия, которому должны удовлетворять полученные на его основе оценки параметров эконометрической модели: сумма квадратов значений фактической ошибки модели должна быть минимальной.

Иными словами, найденные с помощью МНК оценки a₀, a₁,..., a_n, обеспечивают минимум следующей квадратичной формы на множестве всех других комбинаций значений таких оценок:

где e_t – значение фактической ошибки модели в момент t=1,2,..., Т, полученное после подстановки в выражение (1) вместо неизвестных истинных значений параметров ₀, ₁,..., _n их оценок a₀, a₁,..., a_n.

Оптимальные по данному критерию значения оценок в этом случае могут быть найдены путем решения следующей системы так называемых “нормальных” уравнений, вытекающей из условия равенства нулю частных производных функции s² (₀, ₁,..., _n) по своим параметрам в точке минимума:

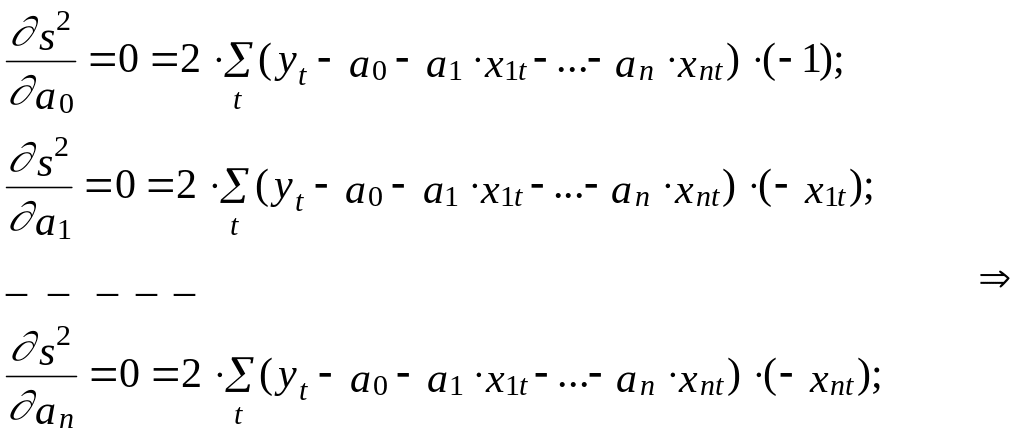
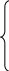
В системе (2.3) неизвестными являются оценки параметров a₀, a₁,..., a_n, а ее известные коэффициенты сформированы на основе исходных данных и представлены в виде следующих сумм: i,j=1,2,..., п. Решения, получаемые на основе развернутой формы системы (2.3), достаточно громоздки, и поэтому в дальнейшем в математических выкладках общего характера будем использовать векторно-матричную форму представления ее составляющих.

Векторно-матричная форма записи линейной эконометрической модели (1) имеет следующий вид:

у=Х+, (2.4)

где у – вектор-столбец, состоящий из Т компонент; Х – матрица размера Т(п+1) (если в модели присутствует “свободный” коэффициент ₀); =(₀, ₁,..., _n)– вектор-столбец параметров, состоящий из п+1-й компоненты;  – вектор-стобец ошибки модели, состоящий, как и вектор у, из Т компонент.

Соответственно векторно-матричный вариант модели, в котором вместо неизвестных истинных коэффициентов  и ошибок  используются их оценки, т. е. вектора а и е, запишем в следующем виде:

у=Ха+е, (2.5)

где а=(а₀, а₁,..., а_n), е=(е₁, е₂,..., е_Т)– вектора значений оценок коэффициентов линейной эконометрической модели и значений ее фактической ошибки соответственно [4, с.175].

Сумму квадратов значений ошибки s² можем представить в виде скалярного произведения вектора-строки е на вектор-столбец е. Проводя несложные преобразования с учетом правил произведения векторов и матриц, получим следующий результат:

s² =(е, е)=(у–Хa)(у–Хa)= уу–aХу–уХa+aХХa=уу–2aХу+aХХa. (2.6)

При проведении преобразований учитывалось правило транспонирования векторно-матричного произведения (zW)=(Wz).

Условие (2.3) в векторной форме записи приобретает следующий вид:

s²/a=0. (2.7)

Заметим, что в выражении (2.7) операция дифференцирования осуществляется по вектору.

С учетом выражения (2.6) уравнение (2.7) приводится к следующему виду:

s²/a=(уу–2aХу+aХХa)/a=–2Ху+2ХХa=0

или ХХa=Ху.

Откуда следует, что “оптимальный” вектор оценок параметров a определяется на основе следующего векторно-матричного выражения:

a=(ХХ)^–1Ху. (2.8)

Все переменные в правой части выражения (2.8) являются известными – это исходные данные, сведенные в матрицу Х и вектор у.

Рассмотрим применение МНК на конкретном примере. Имеются данные о цене на нефть x (долларов за баррель) и индексе акций нефтяной компании y (в процентных пунктах). Требуется найти эмпирическую формулу, отражающую связь между ценой на нефть и индексом акций нефтяной компании исходя из предположения, что связь между указанными переменными линейна и описывается функцией вида yi=β0+β1xi. Зависимой переменной (y) в данной регрессионной модели будет являться индекс акций нефтяной компании, а независимой (x) — цена на нефть.

Для нахождения коэффициентов β0 и β1 построим вспомогательную таблицу 1.

Таблица 1

Таблица для нахождения коэффициентов β0 и β1

№ наблюдения	Цена на нефть – х, ден.ед.	Индекс нефтяной компании - %	xi *yi	хi^2
1	17,28	537	9279,36	298,5984
2	17,05	534	9104,70	290,7025
3	18,30	550	10 065,00	334,8900
4	18,80	555	10 434,00	353,4400
5	19,20	560	10 752,00	368,6400
6	18,50	552	10 212,00	342,2500
Сумма по столбцу	110,13	3288	59 847,06	1988,52

Запишем систему нормальных уравнений исходя из данных таблицы:

1988,52β + 110,13β = 59847,06,

110,13β + 6β = 3288.

Решением данной системы нормальных уравнений будут следующие числа: β1=15,317; β0=266,86. Таким образом, уравнение регрессии, описывающее зависимость между ценой на нефть и индексом акций нефтяной компании, можно записать как: y = 15,317x + 266,86.

На основании полученного уравнения регрессии можно сделать вывод о том, что с изменением цены на нефть на 1 денежную единицу за баррель индекс акций нефтяной компании изменяется примерно на 15,317 процентных пункта.