
№1 Ортогональные функции.
Две
вещественные функции ![]() и
и ![]() на
интервале
на
интервале ![]() называются ортогональными,
если
называются ортогональными,
если

Для комплексных функций вводится комплексное сопряжение одной из функций под интегралом, для векторных — скалярное произведение функций под интегралом, а также интегрирование по отрезку заменяется на интегрирование по области соответствующей размерности.
Полезным
обобщением понятия ортогональности
является ортогональность с определённым
весом. Ортогональны с весом ![]() функции
функции ![]() и
и ![]() ,
если
,
если
![]()
где ![]() —
скалярное произведение векторов
—
скалярное произведение векторов ![]() и
и ![]() —
значений векторнозначных функций
и
в
точке
—
значений векторнозначных функций
и
в
точке ![]() ,
—
точка области
,
—
точка области ![]() ,
а
,
а ![]() —
элемент её объёма (меры).
Эта формула записана наиболее общим
способом по сравнению со всеми выше. В
случае вещественных скалярных
,
скалярное
произведение следует заменить на
обычное; в случае комплексных
скалярных
,
:
—
элемент её объёма (меры).
Эта формула записана наиболее общим
способом по сравнению со всеми выше. В
случае вещественных скалярных
,
скалярное
произведение следует заменить на
обычное; в случае комплексных
скалярных
,
: ![]() .
.
Ряд Фурье по ортогональной системе функций
Определение. Функции j(х) и y(х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если
![]()
Определение. Последовательность функций j1(x), j2(x), …, jn(x), непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если все функции попарно ортогональны.
![]()
Отметим, что ортогональность функций не подразумевает перпендикулярности графиков этих функций.
Определение. Система функций называется ортогональной и нормированной (ортонормированной), если
![]()
Определение. Рядом Фурье по ортогональной системе функций j1(x), j2(x), …,jn(x) называется ряд вида:
![]()
коэффициенты которого определяются по формуле:
 ,
,
где f(x) = - сумма равномерно сходящегося на отрезке [a, b] ряда по ортогональной системе функций. f(x) – любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a, b].
[an error occurred while processing this directive]
В случае ортонормированной системы функций коэффициенты определяются:
![]()
№ 3 разложение в ряды фурье по системе косинусов и синусов
Разложение в ряд Фурье по косинусам.
Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Разложение в ряд Фурье по синусам.
Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,

где коэффициенты ряда Фурье,

№
5 Предел ФКП.
Непрерывность
ФКП. Производная ФКП. Условия
Каши-Римана.
Предел
ФКП.
Определение. Пусть
функция w = f(z)
определена в проколотой окрестности
точки z0 = x0 + iy0.
Комплексное число w0 = u0 + iv0 называется
пределом функции при z → z0,
если для любой ε-окрестности U(w0,
ε) (ε>0) точки w0 найдётся
такая проколотая δ-окрестность ![]() точки z0,
что для всех
точки z0,
что для всех ![]() значения f(z)
принадлежат U(w0,
ε). Другими словами, если z0 -
собственная точка плоскости, то для
любого ε > 0 должно существовать такое
δ > 0, что из неравенства 0 < |z − z0|
< δ следует неравенство | f(z)
− w0|
< ε (аналогично расписывается определение
для несобственной точки z0 =
∞). Таким образом, на языке ε - δ определение
предела ФКП полностью совпадает с
определением предела функции одной
действительной переменной; обозначается
предел, как обычно:
значения f(z)
принадлежат U(w0,
ε). Другими словами, если z0 -
собственная точка плоскости, то для
любого ε > 0 должно существовать такое
δ > 0, что из неравенства 0 < |z − z0|
< δ следует неравенство | f(z)
− w0|
< ε (аналогично расписывается определение
для несобственной точки z0 =
∞). Таким образом, на языке ε - δ определение
предела ФКП полностью совпадает с
определением предела функции одной
действительной переменной; обозначается
предел, как обычно: ![]() .
Неравенство
| f(z)
− w0|
< ε означает, что |(u(x, y)
+ iv(x, y))
− (u0 + iv0)|
< ε, или |(u(x, y)
- u0)
+ i(v(x, y)
− v0)|
< ε. Для модуля комплексных чисел
справедливы все основные свойства
абсолютной величины, в частности
|z1 + z2|
≤ |z1|
+ |z2|,
поэтому |(u(x, y)
- u0)
+ i(v(x, y)
− v0)|
< ε
.
Неравенство
| f(z)
− w0|
< ε означает, что |(u(x, y)
+ iv(x, y))
− (u0 + iv0)|
< ε, или |(u(x, y)
- u0)
+ i(v(x, y)
− v0)|
< ε. Для модуля комплексных чисел
справедливы все основные свойства
абсолютной величины, в частности
|z1 + z2|
≤ |z1|
+ |z2|,
поэтому |(u(x, y)
- u0)
+ i(v(x, y)
− v0)|
< ε Отсюда
легко получить, что
Отсюда
легко получить, что ![]()
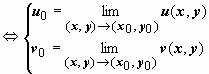 .
Таким образом, существование предела
функции комплексной переменной
равносильно существованию пределов
двух действительных функций u(x, y)
и v(x, y)
двух действительных переменных. Поэтому
в комплексный анализ автоматически
переносятся все теоремы о пределах
функции в точке (предел суммы функций
и т.д.). Так же можно доказать, что если w0 =
|w0|·(cos
arg w0 + i sin
arg w0)
≠ 0, то
.
Таким образом, существование предела
функции комплексной переменной
равносильно существованию пределов
двух действительных функций u(x, y)
и v(x, y)
двух действительных переменных. Поэтому
в комплексный анализ автоматически
переносятся все теоремы о пределах
функции в точке (предел суммы функций
и т.д.). Так же можно доказать, что если w0 =
|w0|·(cos
arg w0 + i sin
arg w0)
≠ 0, то  (для
существования нулевого предела
достаточно, чтобы
(для
существования нулевого предела
достаточно, чтобы![]() ). .
). .
Непрерывность
ФКП. Пусть
функция w = f(z)
определена в окрестности точки z0 = x0 + iy0.
Функция называется непрерывной в
точке z0,
если:
1.
существует ![]() ;
2.
;
2. ![]() Как
и в случае предела, можно показать,
что w = f(z)
будет непрерывной в точке z0 = x0 + iy0 тогда
и только тогда, когда функции u(x, y)
и v(x, y)
непрерывны в точке (x0, y0),
поэтому на ФКП переносятся все основные
теоремы о непрерывности функций.
Как
и в случае предела, можно показать,
что w = f(z)
будет непрерывной в точке z0 = x0 + iy0 тогда
и только тогда, когда функции u(x, y)
и v(x, y)
непрерывны в точке (x0, y0),
поэтому на ФКП переносятся все основные
теоремы о непрерывности функций.
Определение
производной. Аналитичность
ФКП. Пусть w = f(z)
определена, однозначна и принимает
собственные значения в окрестности
точки z = x + iy ∈ C.
Производной функции w = f(z)
в точке z называется
предел ![]() .
Функция, имеющая конечную производную
в точке z,
называется дифференцируемой в этой
точке.
В
этом определении важно, что стремление
Δz →
0 может проходить по любому пути. Как мы
увидим дальше, вследствие этого
обстоятельства существование
производной f’(z)
не сводится к существованию частных
производных функций u(x, y)
и v(x, y),
а требует некоторых дополнительных
условий. Сейчас мы дадим определение
основного в теории ФКП понятия
-аналитичности
функции в
точке и в области.
Определение.
Однозначная функция называется аналитической
(регулярной, голоморфной) в
точке z,
если она дифференцируема в некоторой
окрестности этой точки.
Однозначная
функция называется аналитической в
области D, если
она аналитична в каждой точке этой
области.
Примеры. 1. f(z)
= z 2. В
этом случае f (z +
Δz)
= (z +
Δz)2 = z 2 +
2 z·Δz +
(Δz) 2;
.
Функция, имеющая конечную производную
в точке z,
называется дифференцируемой в этой
точке.
В
этом определении важно, что стремление
Δz →
0 может проходить по любому пути. Как мы
увидим дальше, вследствие этого
обстоятельства существование
производной f’(z)
не сводится к существованию частных
производных функций u(x, y)
и v(x, y),
а требует некоторых дополнительных
условий. Сейчас мы дадим определение
основного в теории ФКП понятия
-аналитичности
функции в
точке и в области.
Определение.
Однозначная функция называется аналитической
(регулярной, голоморфной) в
точке z,
если она дифференцируема в некоторой
окрестности этой точки.
Однозначная
функция называется аналитической в
области D, если
она аналитична в каждой точке этой
области.
Примеры. 1. f(z)
= z 2. В
этом случае f (z +
Δz)
= (z +
Δz)2 = z 2 +
2 z·Δz +
(Δz) 2; ![]() . Таким
образом , эта функция дифференцируема
в любой точке, и её производная равна
2z.
. Таким
образом , эта функция дифференцируема
в любой точке, и её производная равна
2z.
 2. f(z)
= | z |2 = x2 + y2. Докажем,
что эта функция не имеет производной
ни в какой точке z ≠
0. Будем стремить Δz →
0 по двум путям: по прямой, параллельной
действительной оси Ох (в
этом случае Δz =
Δx),
и по прямой, параллельной мнимой оси Оу (в
этом случае Δz = i Δy).
В первом случае
2. f(z)
= | z |2 = x2 + y2. Докажем,
что эта функция не имеет производной
ни в какой точке z ≠
0. Будем стремить Δz →
0 по двум путям: по прямой, параллельной
действительной оси Ох (в
этом случае Δz =
Δx),
и по прямой, параллельной мнимой оси Оу (в
этом случае Δz = i Δy).
В первом случае ![]() , во
втором
, во
втором ![]()
![]() . Эти
пределы равны, только если 2х =
−2iy ⇒ х = y =
0. Таким образом, функция f(z)
= | z |2 = x2 + y2 может
быть дифференцируема в единственной
точке z =
0, во всех остальных точках пределы
. Эти
пределы равны, только если 2х =
−2iy ⇒ х = y =
0. Таким образом, функция f(z)
= | z |2 = x2 + y2 может
быть дифференцируема в единственной
точке z =
0, во всех остальных точках пределы ![]() различны
в зависимости от способа стремления
Δz →
0, т.е.
различны
в зависимости от способа стремления
Δz →
0, т.е. ![]() не
существует.
не
существует.
Условия
Коши-Римана (Даламбера-Эйлера).Сейчас
мы сформулируем и докажем важнейшую в
теории ФКП теорему о необходимых и
достаточных условиях дифференцируемости
(а, следовательно, аналитичности)
функции.
Для
того, чтобы функция w = f(z)
= u(x, y)
+ i v(x, y)
была дифференцируема в точке z = x + iy,
необходимо и достаточно, чтобы
функции u(x, y)
= Re f(z) и v(x, y)
= Im f(z)
были дифференцируемы в точке (х,у), и
чтобы в этой точке выполнялись
соотношения  .
Доказательство. Необходимость. Здесь
мы применим идею, которой воспользовались,
когда доказывали, что функция f(z)
= | z |2 = x2 + y2 не
имеет производных в точках z ≠
0: подойдём к точке z двумя
путями - по направлениям Δz =
Δх (Δy =
0) и Δz = iΔy (Δx =
0).
В
первом случае: Δw =
(u(x +
Δx, y)
+ iv(x +
Δx, y))
− (u(x, y)
+ iv(x, y))
=
=
(u(x +
Δx, y)
− u(x, y))
+ i(v(x +
Δx, y)
− v(x, y))
= Δxu + iΔxv;
.
Доказательство. Необходимость. Здесь
мы применим идею, которой воспользовались,
когда доказывали, что функция f(z)
= | z |2 = x2 + y2 не
имеет производных в точках z ≠
0: подойдём к точке z двумя
путями - по направлениям Δz =
Δх (Δy =
0) и Δz = iΔy (Δx =
0).
В
первом случае: Δw =
(u(x +
Δx, y)
+ iv(x +
Δx, y))
− (u(x, y)
+ iv(x, y))
=
=
(u(x +
Δx, y)
− u(x, y))
+ i(v(x +
Δx, y)
− v(x, y))
= Δxu + iΔxv; ![]() .
Во
втором случае: (напомню, что
.
Во
втором случае: (напомню, что ![]() )
Δw =
(u(x, y +
Δy)
+ iv(x, y +
Δy))
− (u(x, y)
+ iv(x, y))
=
=
(u(x, y +
Δy)
− u(x, y))
+ i(v(x, y +
Δy)
− v(x, y))
= Δyu + iΔyv;
)
Δw =
(u(x, y +
Δy)
+ iv(x, y +
Δy))
− (u(x, y)
+ iv(x, y))
=
=
(u(x, y +
Δy)
− u(x, y))
+ i(v(x, y +
Δy)
− v(x, y))
= Δyu + iΔyv; ![]() .
Пределы должны быть равны,
поэтому
.
Пределы должны быть равны,
поэтому ![]() .
Достаточность. По
предположению теоремы, функции u(x, y), v(x, y)
дифференцируемы в точке (х,у),
поэтому
.
Достаточность. По
предположению теоремы, функции u(x, y), v(x, y)
дифференцируемы в точке (х,у),
поэтому ![]() где
α(Δx,
Δy),
β(Δx,
Δy)
- бесконечно малые более высокого порядка
по сравнению с
где
α(Δx,
Δy),
β(Δx,
Δy)
- бесконечно малые более высокого порядка
по сравнению с ![]() ,
т.е.
,
т.е. ![]() ,
, ![]() .
Найдём
.
Найдём ![]() .
. ![]()
![]() .
Последнее
слагаемое - бесконечно малая высшего
порядка по сравнению с Δz =
Δx + iΔy:
.
Последнее
слагаемое - бесконечно малая высшего
порядка по сравнению с Δz =
Δx + iΔy: ![]() ;
далее, в предыдущих слагаемых, пользуясь
формулами Коши-Римана, оставим только
частные производные по х,
т.е. заменим
;
далее, в предыдущих слагаемых, пользуясь
формулами Коши-Римана, оставим только
частные производные по х,
т.е. заменим ![]() на
на ![]() ,
, ![]() на
на ![]() ;
тогда
;
тогда 
![]() .
Отсюда следует, что существует
.
Отсюда следует, что существует ![]() ,
т.е. функция дифференцируема в точке
(х,у).
Производная
дифференцируемой функции может находиться
по любой из формул
,
т.е. функция дифференцируема в точке
(х,у).
Производная
дифференцируемой функции может находиться
по любой из формул ![]() ,
эти равенства следуют из условий
Коши-Римана. При вычислении производных
можно пользоваться всеми правилами
действительного анализа:
,
эти равенства следуют из условий
Коши-Римана. При вычислении производных
можно пользоваться всеми правилами
действительного анализа:  (в
точках, где g(z)
≠ 0.
(в
точках, где g(z)
≠ 0.
№ 7. Вычеты и их приложения. Основная теорема теории вычетов.
основная
теорема о вычетах: если
функция ![]() является
аналитической всюду в замкнутой
области
является
аналитической всюду в замкнутой
области ![]() ,
за исключением конечного числа
изолированных особых точек
,
за исключением конечного числа
изолированных особых точек ![]() ,
лежащих внутри
,
то
,
лежащих внутри
,
то
|
Пример:
Вычислить интеграл  .
.
Решение:
Точка ![]() является
особой для подынтегральной функции,
причем, согласно классификации, это
полюс третьего порядка. Тогда
является
особой для подынтегральной функции,
причем, согласно классификации, это
полюс третьего порядка. Тогда
![]()
и
соответственно  .
.

