Множества.

Множеством назыв. совокупность однородных элементов (объектов), удовлетворяя некоторому свойству, кот. назыв. характеристическим свойством множества. (Множество A,B)

Объекты, из кот. состоят множества назыв. элементами.

Множество A назыв. подмножеством множества B, если все элементы A явл. элементами B. (A∈ B)

Множество назыв. пустым, если оно не содержит элементов.

Множество назыв. конечным, если оно содержит конечное число элементов, например, множество целых чисел от 0 до 10.

Если число элементов множества бесконечно, то данное множество назыв. бесконечным. Например, бесконечным явл. множество точек отрезка чисел прямой A,B.

Если каждому элементу множества A можно поставить в соответствие единственный элемент множества B, и наоборот, то между этими множествами существует взаимооднозначное соответствие.

Множество A наз. счетным, если каждому его элементу можно поставить в соответствие натуральное число.

Операции над множествами.

1. Объединением множеств A и B назыв. множество элементов либо мн-а A, либо мн-ва B, либо и A, и B. (A∪B)

2. Пересечением множеств A и B назыв. множество элементов, кот. явл. и элементами мн-а A, и элементами мн-ва B. (A∩B)

3. Разностью множеств A\B наз. множество элементов мн-ва A, кот. не явл. мн-вом B.

4. Пусть заданы 2 множества A и B, причем A включается в B. Дополнением мн-ва A наз. множество элементов мн-а B, кот. не входит в A.

5. Декартовым произведением мн-ва A и B наз. множество C=A·B, состоящее из упорядоченных пар (a:b), причем a∈A, b∈B.

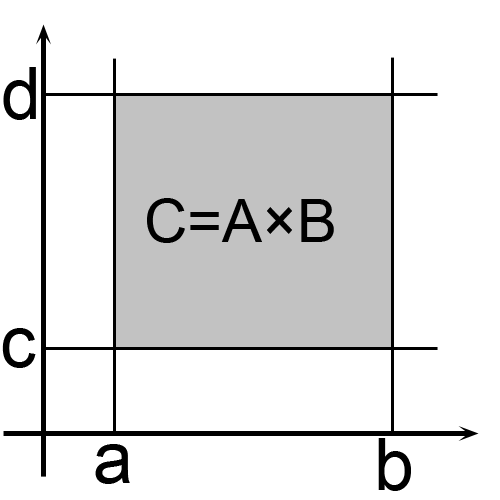
Предположим, что A∈[a;b]; B∈[c;d].

Квантор общности ∀x ∈ X (для любого x из мн-ва X)

Квантор существования ∃n ∈ N (существ. натуральное число n)

Числовые множества. Грани множеств.

Числовыми множествами наз. мн-ва, элементами кот. являются числа.

N={1;2…} – множество натуральных чисел

Z={0;±1;±2…} – множество целых чисел

Q={m/n; m∈Z: n∈N} – множество рациональных чисел

R=(-∞; +∞) – множество действительных чисел

Число K наз. верхней гранью мн-ва A, если для любого ∀x ∈ A выполняется неравенство x ≤ K

Число K наз. нижней гранью мн-ва A, если для любого ∀x ∈ A выполняется неравенство x ≥ K

Любое множество имеет мн-во верхних или нижних граней.

Наибольшая из нижних частей множества называется точной нижней гранью множества или инфимумом. (infA)

Наименьшая из верхних частей множества называется точной верхней гранью множества или супремумом. (supA)

A={1/n; n∈N}, supA=1, infA=0.

Последовательности.

Пусть заданы 2 множества x и y.

Говорят, что на множестве x задана функция y=f(x), если существует некоторое правило, по которому каждому элементу из множества x ставится в соответствие элемент из множества y.

Т .е. ф-ия есть соотношение между двумя множествами.

x – область определения D(t)

y – область значений E(t)

Числовой последовательностью, обозн. {x_n}^∞_n=1, назыв. функция натурального аргумента.

Задать числовую последовательность – это значит задать правило, по кот. каждому натуральному числу n ставится в соответствие некоторый член числовой последовательности.

Пример: ; n=3 ⇒ - числовые посл-ти чаще всего задаются в виде общего члена.

Ограниченные последовательности.

1. Посл-ть x_n называется огранич. сверху, если сущ. некоторое действительное число M, такое, что все элементы последовательности не превосходят этого числа.

{x_n}^∞_n>1 - огр. сверху  ∃M ∈ R ∀n ∈ N x_n ≤ M

2. Посл-ть x_n называется огранич. снизу, если сущ. некоторое действительное число M, такое, что любой

член последовательности ≥ M.

{x_n}^∞_n=1 - огр. снизу  ∃M ∈ R ∀n ∈ N x_n ≥ M

3. Посл-ть x_n называется ограниченной, если она ограничена сверху и снизу, т.е. сущ. некоторое число

M ≠0, такое, что любой член посл-ти ≤ M.

Монотонные последовательности.

Посл-ть наз. постоянной, если все ее члены равны.

Посл-ть наз. возрастающей, если для любого натурального n каждый последующий член больше предыдущего. ∀n ∈ N x_n+1 > x_n

Посл-ть наз. убывающей, если для любого натурального n каждый последующий член меньше предыдущего. ∀n ∈ N x_n+1 < x_n

Посл-ть Xn наз. невозрастающей, если ∀n ∈ N x_n+1 ≤ x_n

Посл-ть Xn наз. неубывающей, если ∀n ∈ N x_n+1 ≥ x_n

Посл-ть наз. монотонной, если она является возрастающей или убывающей

Предел посл-ти.

Число a наз. пределом числа посл-ти {x_n}, если для любого как угодно малого положит. числа E сущ. зависящий от него Ne, начиная с кот. все члены посл-ти удовлетворяют неравенству |x_n – a| < E

lim_n→∞ x_n = a  ∀e > 0 ∃Ne ∀n>Ne | x_n – a| < E

ε-окрестностью т. a (Oε(a)) наз. интервал (a-ε ; a+ε)

Проколотой ε-окрестностью т. a наз. объединение интервалов Oφ (a) = (a-φ ; a) ∪(a ; a+φ)

Геометрический смысл предела: то, что число a является пределом числовой посл-ти x_n с геометрической точки зрения означает, что какое бы бесконечно малое число ε мы не выбрали, обязательно найдется номер числа числ. последовательности (Na), начиная с кот. ВСЕ члены посл-ти попадают внутрь ε-окрестности т.a, т.е. при любом ε вне Oφ (a) расположено только конечное число членов посл-ти, а внутри ее их бесконечное число.

Посл-ть, имеющая конечный предел, наз. сходящейся.

Критерий существ. предела посл-ти: если посл-ть x_n монотонно возрастающая (убывающая) и ограничена сверху (снизу), то она имеет предел, равный значению точной верхней (нижней) грани. Справедливо и обратное.

Бесконечно малые посл-ти.

Посл-ть x_n наз. БМП, если её предел =0, т.е. ∀E>0 ∃Ne; n>Ne, |x_n|<E

Свойства БМП:

1. Сумма конечного числа БМП есть БМП

2. Произведение огранич. посл-ти на БМП есть БМП

3. Произведение сходящейся посл-ти на БМП есть БМП

4. Произведение БМП-тей есть БМП

Замечание: при делении двух БМП полученная посл-ть необязательно явл. БМП. В этом случае возникает неопределенность вида 0/0. В результате, раскрыв данную неопр-ть, мы можем получить как число (0 тоже), так и бесконечность.

Бесконечно большие посл-ти.

Посл-ти, имеющие lim = ∞ наз. расходящимися или ББП.

Посл-ть x_n наз. ББП, если lim_n→∞ x_n = ∞, т.е. для любого как угодно большого числа K существует некоторый номер, зависящий от К, начиная с кот. все члены посл-ти удовлетворяют неравенству |x_n|>K:

Xn – ББП, если lim_n→∞ x_n  ∀k > 0 ∃Nk ∀n>Nk |x_n| < K

Теорема (связь между сходящейся посл-тью и БМП): посл-ть x_n имеет lim_n→∞ =a, тогда и только тогда, когда она представлена в виде суммы x_n = a+Α_n, где A_n – БМП.

Теорема (связь между ББП и БМП): если посл-ть A_n – БМП, то посл-ть B_n=1/A_n явл. ББП; если посл-ть B_n – ББП, то A_n=1/B_n – БМП.

Свойства сходящихся посл-тей:

1. Теорема о единственности предела: если x_n имеет конечный предел, то он единственен.

2. Пусть заданы 2 сходящиеся посл-ти: x_n, имеющая lim_n→∞ =a и посл-ть y_n, имеющая lim_n→∞ =b, тогда:

1. (x_n ± y_n) также явл. сходящейся, причем lim_n→∞(x_n ± y_n) = lim_n→∞x_n ± lim_n→∞y_n = a ± b

2. (k · x_n) явл. сходящейся, причем lim_n→∞(k · x_n) = k · a

3. (x_n · y_n) явл. сходящейся, причем lim_n→∞(x_n · y_n) = lim_n→∞x_n

4. Если посл-ть y_n не явл. тожд. ≠ 0 и b≠0, то (x_n/y_n) явл. сходящейся, причем lim_n→∞(x_n/y_n) = lim_n→∞x_n/lim_n→∞y_n = a/b

3. Предел постоянной посл-ти равен самой постоянной.

Теоремы о переходе к пределу в неравенствах.

1. Пусть задана некоторая сходящаяся посл-ть x_n, для кот. известно, что все ее члены кроме, быть может, конечного числа членов, больше 0. Тогда lim_n→∞x_n ≥ 0.

Замечание: аналогичную теорему можно сформулировать для посл-ти с отрицательными членами. Тогда lim_n→∞x_n ≤ 0.

2. Пусть заданы 2 сходящиеся посл-ти: x_n; lim _n→∞ x_n = a и y_n; lim _n→∞ y_n = b. Если члены посл-ти удовлетворяют неравенству x_n<y_n, то lim _n→∞ x_n ≥ lim _n→∞ y_n.

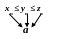3. Т еорема о двух милиционерах. Пусть заданы 3 посл-ти: x_n, y_n, z_n, причем посл-ти x_n и z_n явл. сходящимися и их предел = a. Если для членов посл-ти справедливо неравенство x_n≤y_n≤ z_n, то посл-ть y_n также явл. сходящейся и lim _n→∞ y_n = a.

Второй замечательный предел.

Рассмотрим x_n = (1+1/n)ⁿ и найдем предел данной последовательности. Данная посл-ть представляет собой неопределенность вида 1^∞ . lim _n→∞(1+1/n)ⁿ = e ≈ 2,12.

Правила раскрытия неопределенности ∞/∞

lim _n→∞Pk(n) / Qm(n)

Для того, чтобы раскрыть неопр-ть ∞/∞ при делении многочленов прежде всего необходимо определить степени этих многочленов:

1. Если степень многочлена в числителе = степени многочлена в знаменателе, то предел = отношению старших коэффициентов, т.е. чисел при старших степенях.

2. Если степень числителя > степени знаменателя, то lim=∞.

3. Если степень числителя < степени знаменателя, то lim=0.