
- •Ответы к экзамену по математическому анализу
- •Основные определения и задачи теории дифференциальных уравнений. Дифференциальные уравнения первого порядка. Теорема и задача Коши.
- •Дифференциальные уравнения с разделяющимися переменными.
- •Однородные дифференциальные уравнения первого порядка.
- •Линейные дифференциальные уравнения первого порядка и уравнения Бернулли. Дифференциальные уравнения в полных дифференциалах. Линейные дифференциальные уравнения первого порядка
- •5. Дифференциальные уравнения второго и высших порядков.
- •6. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •7. Линейные дифференциальные уравнения второго порядка. Однородные уравнения. Определитель Вронского. Фундаментальная система решений.
- •8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •9. Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами и специальной правой частью.
- •10.Решение линейного дифференциального уравнения 2-го порядка методом Лагранжа.
- •11. Системы дифференциальных уравнений. Решение нормальной линейной системы методом характеристического уравнения.
- •– Линейные однородные системы дифференциальных уравнений – Линейные неоднородные системы дифференциальных уравнений
- •Линейные однородные системы дифференциальных уравнений
- •Что значит решить систему дифференциальных уравнений?
- •Линейные неоднородные системы дифференциальных уравнений
- •Метод характеристического уравнения (метод Эйлера)
- •12. Числовые ряды: основные определения. Геометрическая прогрессия как пример числового ряда. Основные определения и понятия.
- •13. Гармонический ряд. Необходимый признак сходимости ряда. Признаки сравнения для определения сходимости рядов с положительными членами. Числовые ряды
- •Необходимый признак сходимости ряда.
- •Достаточные признаки сходимости ряда с положительными членами
- •1. Признак Даламбера
- •2. Интегральный признак Коши
- •3. Признак сравнения рядов
- •14. Признаки сходимости Даламбера и Коши для рядов с положительными членами. Обобщенно гармонический ряд. Признак Даламбера. Радикальный признак Коши.
- •Обобщённо гармонический ряд. Ряд Дирихле:
- •Знакопеременный ряд:
- •15. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.
- •16. Функциональные ряды. Точки и область сходимости. Функциональные ряды
- •17. Степенные ряды и область сходимости. Степенные ряды
- •18. Разложение функций в ряды Тейлора и Маклорена.
- •19. Применения рядов Тейлора для приближенных вычислений интегралов и решений дифференциальных уравнений.
- •20. Ряд Фурье и его коэффициенты.
- •21. Разложение функции в ряд Фурье. Теорема Дирихле.
- •22. Определение и свойства двойного интеграла.
- •23. Вычисление двойных интегралов.
- •24. Замена переменных в двойном интеграле. Полярные координаты.
- •25.Приложения двойного интеграла.
- •26. Определение тройного интеграла.
- •27. Вычисление тройного интеграла.
- •28. Замена переменных в тройном интеграле. Цилиндрические координаты.
- •29. Вычисление тройного интеграла в сферических координатах.
- •Решение
Ответы к экзамену по математическому анализу
Основные определения и задачи теории дифференциальных уравнений. Дифференциальные уравнения первого порядка. Теорема и задача Коши.
Дифференциальное
уравнение (ДУ)
– это уравнение, в которое входит
неизвестная функция под знаком производной
или дифференциала.
Если неизвестная
функция является функцией одной
переменной, то дифференциальное уравнение
называют обыкновенным
(сокращенно ОДУ – обыкновенное
дифференциальное уравнение). Если же
неизвестная функция есть функция многих
переменных, то дифференциальное уравнение
называют уравнением
в частных производных.
Максимальный
порядок производной неизвестной функции,
входящей в дифференциальное уравнение,
называется порядком
дифференциального уравнения.
Вот
примеры ОДУ первого, второго и пятого
порядков соответственно
 В
качестве примеров уравнений в частных
производных второго порядка
приведем
В
качестве примеров уравнений в частных
производных второго порядка
приведем
 Далее
мы будем рассматривать только обыкновенные
дифференциальные уравнения n-ого
порядка вида
Далее
мы будем рассматривать только обыкновенные
дифференциальные уравнения n-ого
порядка вида
 или
или
 ,
где Ф(x,
y) = 0
неизвестная функция, заданная неявно
(когда возможно, будем ее записывать в
явном представлении y
= f(x)).
Процесс
нахождения решений дифференциального
уравнения называется интегрированием
дифференциального уравнения.
Решение
дифференциального уравнения
- это неявно заданная функция Ф(x,
y) = 0
(в некоторых случаях функцию y
можно выразить через аргумент x
явно), которая обращает дифференциальное
уравнение в тождество.
ОБРАТИТЕ
ВНИМАНИЕ.
Решение дифференциального
уравнения всегда ищется на заранее
заданном интервале X.
Почему
мы об этом говорим отдельно? Да потому
что в условиях многих задач об интервале
X
не упоминают. То есть, обычно условие
задач формулируется так: «найдите
решение обыкновенного дифференциального
уравнения
».
В этом случае подразумевается, что
решение следует искать для всех x,
при которых и искомая функция y,
и исходное уравнение имеют смысл.
Решение дифференциального
уравнения часто называют интегралом
дифференциального уравнения.
Функции
,
где Ф(x,
y) = 0
неизвестная функция, заданная неявно
(когда возможно, будем ее записывать в
явном представлении y
= f(x)).
Процесс
нахождения решений дифференциального
уравнения называется интегрированием
дифференциального уравнения.
Решение
дифференциального уравнения
- это неявно заданная функция Ф(x,
y) = 0
(в некоторых случаях функцию y
можно выразить через аргумент x
явно), которая обращает дифференциальное
уравнение в тождество.
ОБРАТИТЕ
ВНИМАНИЕ.
Решение дифференциального
уравнения всегда ищется на заранее
заданном интервале X.
Почему
мы об этом говорим отдельно? Да потому
что в условиях многих задач об интервале
X
не упоминают. То есть, обычно условие
задач формулируется так: «найдите
решение обыкновенного дифференциального
уравнения
».
В этом случае подразумевается, что
решение следует искать для всех x,
при которых и искомая функция y,
и исходное уравнение имеют смысл.
Решение дифференциального
уравнения часто называют интегралом
дифференциального уравнения.
Функции
 или
или
 можно
назвать решением дифференциального
уравнения
можно
назвать решением дифференциального
уравнения
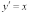 .
Одним
из решений дифференциального уравнения
.
Одним
из решений дифференциального уравнения
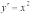 является
функция
является
функция
 .
Действительно, подставив эту функцию
в исходное уравнение, получим тождество
.
Действительно, подставив эту функцию
в исходное уравнение, получим тождество
 .
Несложно заметить, что другим решением
этого ОДУ является, например,
.
Несложно заметить, что другим решением
этого ОДУ является, например,
 .
Таким образом, дифференциальные уравнения
могут иметь множество решений.
Общее
решение дифференциального уравнения
– это множество решений, содержащее
все без исключения решения этого
дифференциального уравнения.
Общее
решение дифференциального уравнения
еще называют общим
интегралом дифференциального
уравнения.
Вернемся
к примеру. Общее решение дифференциального
уравнения
имеет
вид
.
Таким образом, дифференциальные уравнения
могут иметь множество решений.
Общее
решение дифференциального уравнения
– это множество решений, содержащее
все без исключения решения этого
дифференциального уравнения.
Общее
решение дифференциального уравнения
еще называют общим
интегралом дифференциального
уравнения.
Вернемся
к примеру. Общее решение дифференциального
уравнения
имеет
вид
 или
или
 ,
где C
– произвольная постоянная. Выше мы
указали два решения этого ОДУ, которые
получаются из общего интеграла
дифференциального уравнения
при
подстановке С
= 0
и C
= 1
соответственно.
Если решение
дифференциального уравнения удовлетворяет
изначально заданным дополнительным
условиям, то его называют частным
решением дифференциального
уравнения.
Частным
решением дифференциального уравнения
,
удовлетворяющим условию y(1)
= 1,
является
,
где C
– произвольная постоянная. Выше мы
указали два решения этого ОДУ, которые
получаются из общего интеграла
дифференциального уравнения
при
подстановке С
= 0
и C
= 1
соответственно.
Если решение
дифференциального уравнения удовлетворяет
изначально заданным дополнительным
условиям, то его называют частным
решением дифференциального
уравнения.
Частным
решением дифференциального уравнения
,
удовлетворяющим условию y(1)
= 1,
является
 .
Действительно,
.
Действительно,
 и
и
 .
Основными
задачами теории дифференциальных
уравнений являются задачи Коши, краевые
задачи и задачи нахождения общего
решения дифференциального уравнения
на каком-либо заданном интервале
X.
Задача
Коши
– это задача нахождения частного решения
дифференциального уравнения,
удовлетворяющего заданным начальным
условиям
.
Основными
задачами теории дифференциальных
уравнений являются задачи Коши, краевые
задачи и задачи нахождения общего
решения дифференциального уравнения
на каком-либо заданном интервале
X.
Задача
Коши
– это задача нахождения частного решения
дифференциального уравнения,
удовлетворяющего заданным начальным
условиям
 ,
где
,
где
 -
числа.
Краевая
задача
– это задача нахождения частного решения
дифференциального уравнения второго
порядка, удовлетворяющего дополнительным
условиям в граничных точках x0
и x1
:
f
(x0)
= f0
, f
(x1)
= f1
, где f0
и f1
- заданные числа.
Краевую задачу
часто называют граничной
задачей.
Обыкновенное дифференциальное
уравнение n-ого
порядка называется линейным,
если оно имеет вид
-
числа.
Краевая
задача
– это задача нахождения частного решения
дифференциального уравнения второго
порядка, удовлетворяющего дополнительным
условиям в граничных точках x0
и x1
:
f
(x0)
= f0
, f
(x1)
= f1
, где f0
и f1
- заданные числа.
Краевую задачу
часто называют граничной
задачей.
Обыкновенное дифференциальное
уравнение n-ого
порядка называется линейным,
если оно имеет вид
 ,
а коэффициенты
,
а коэффициенты
 есть
непрерывные функции аргумента x
на интервале интегрирования.
Если
есть
непрерывные функции аргумента x
на интервале интегрирования.
Если
 ,
то уравнение
называют
линейным
однородным дифференциальным уравнением
(ЛОДУ),
в противном случае – линейным
неоднородным дифференциальным уравнением
(ЛНДУ).
Когда
коэффициенты
,
то уравнение
называют
линейным
однородным дифференциальным уравнением
(ЛОДУ),
в противном случае – линейным
неоднородным дифференциальным уравнением
(ЛНДУ).
Когда
коэффициенты
 являются
постоянными функциями (то есть, некоторыми
числами), то соответствующие дифференциальные
уравнения называют ЛОДУ
с постоянными коэффициентами
(если
)
или ЛНДУ
с постоянными коэффициентами
(при ненулевой f(x)).
Характеристическое
уравнение
линейного однородного дифференциального
уравнения n-ой
степени с постоянными коэффициентами
– это уравнение n-ой
степени вида
являются
постоянными функциями (то есть, некоторыми
числами), то соответствующие дифференциальные
уравнения называют ЛОДУ
с постоянными коэффициентами
(если
)
или ЛНДУ
с постоянными коэффициентами
(при ненулевой f(x)).
Характеристическое
уравнение
линейного однородного дифференциального
уравнения n-ой
степени с постоянными коэффициентами
– это уравнение n-ой
степени вида

F(x, y, y ') = 0,
где y = y(x) — неизвестная, непрерывно дифференцируема на (a, b) функция, называется обыкновенным дифференциальным уравнением первого порядка. Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) . График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения. Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия. Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей). Условие y(x0) = y0 — начальное условие. Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения. Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения. Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения. Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:

Уравнения первого порядка часто записывают в дифференциальной форме:
M(x, y)dx + N(x, y)dy = 0.
Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .
Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка
 или
или


Задачей Коши для для этой системы называется следующая задача: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x0)=Y0, где Y0 — некоторый постоянный вектор.
Справедлива следующая теорема о существовании и единственности решения задачи Коши.
Теорема Коши. Пусть в области D из Rn+1 непрерывны все компоненты вектора правой части F(x,Y) и их частные производные по Y:

Тогда, какова бы ни была начальная точка (x0,Y0) ≡ (x0,y1, 0 ,y2, 0, … ,yn, 0 ) ∈ D , существует такой отрезок [x0 − h; x0 + h] , что задача Коши Y' = F(x,Y), что Y(x0)=Y0 имеет единственное решение.
Важно понимать, что теорема Коши имеет локальный характер: существование решения Y = Y(x) гарантируется лишь в достаточно малой окрестности точки x0 , ( h > 0 может оказаться достаточно малым).
Важно также понимать, что теорема содержит только достаточные условия существования и единственности решения — при нарушении условий теоремы задача Коши может иметь или не иметь решений, может иметь несколько решений.
