
- •Числовые ряды Числовой ряд. Общий член ряда
- •Сходящиеся и расходящиеся ряды
- •Основные свойства сходящихся рядов
- •Признаки сходимости числовых рядов
- •Необходимый признак сходимости ряда
- •Если , то ряд расходится.
- •Знакоположительные числовые ряды
- •Достаточные признаки сходимости знакоположительных рядов
- •Знакочередующиеся и знакопеременные ряды Знакочередующиеся ряды
- •Знакопеременные ряды
- •Функциональные ряды Функциональный ряд и его область сходимости
- •Степенные ряды
- •Геометрическая интерпретация теоремы Абеля
- •Разложение элементарных функций в степенные ряды
- •Приближенные вычисления с помощью степенных рядов
- •Приближенное вычисление корней
- •Приближенное вычисление определенных интегралов
- •Приближенное решение дифференциальных уравнений
- •Теоретические вопросы
- •Расчетные задания
Числовые ряды Числовой ряд. Общий член ряда
Определение.
Пусть дана бесконечная последовательность
чисел
![]() ,
,
![]() ,
,
![]() ,...,
то выражение вида
,...,
то выражение вида
![]() (1)
(1)
называется
числовым
рядом,
числа
,
,
,...–
членами (элементами) ряда,
![]() –
общим членом ряда, если
–
общим членом ряда, если
![]() не зафиксировано.
не зафиксировано.
Пример1.
Дан ряд
![]() ,
где
общий член
,
где
общий член
![]() .
Найти
.
Найти
![]() .
Заменяя в общем члене
на
.
Заменяя в общем члене
на
![]() ,
получим
,
получим
![]() .
.
Сходящиеся и расходящиеся ряды
Сумма
первых n
членов ряда (1) называется
![]() ой
частичной суммой
и обозначается через
ой
частичной суммой
и обозначается через
![]() .
Следовательно, суммы
.
Следовательно, суммы
![]() – 1-ая
частичная сумма;
– 1-ая
частичная сумма;
![]() – 2-ая
частичная сумма;
– 2-ая
частичная сумма;
![]() – 3-ая
частичная сумма;
– 3-ая
частичная сумма;
– ……………………….
![]() –
ая
частичная сумма;
–
ая
частичная сумма;
... – ……………………….
образуют
последовательность частичных сумм
![]() ,
,
![]() ,
...,
,
...,
![]() ,
...
,
...
Определение
Ряд
(1) называется сходящимся,
если существует конечный предел
последовательности частичных сумм, то
есть
![]() .
При этом число
.
При этом число
![]() называется суммой
ряда.
Если для данного ряда последовательность
частичных сумм
называется суммой
ряда.
Если для данного ряда последовательность
частичных сумм
![]() не имеет конечного предела при
не имеет конечного предела при
![]() ,
то этот ряд называется расходящимся.
,
то этот ряд называется расходящимся.
Пример2. Исследовать на сходимость ряд, составленный из членов геометрической прогрессии (геометрический ряд)
![]() ,
,
![]() .
.
Из
элементарной математики известно, что
сумма n
членов геометрической прогрессии
![]() .
Отсюда следует, что если
,
то геометрический ряд сходится и его
сумма
.
Отсюда следует, что если
,
то геометрический ряд сходится и его
сумма
![]() .
Если же
.
Если же
![]() ,
то геометрический ряд расходится.
,
то геометрический ряд расходится.
Пример3.
Исследовать на сходимость ряд
![]() .Так
как
.Так
как
![]() ,
то
ая
частичная сумма данного ряда
,
то
ая
частичная сумма данного ряда
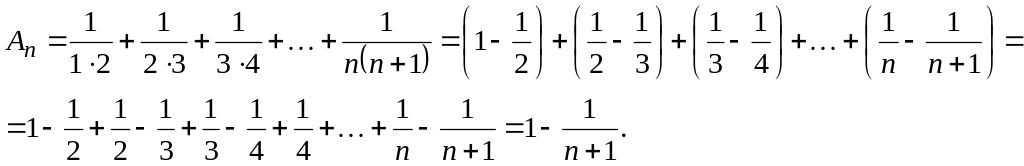
Эта
сумма при
![]() имеет предел
имеет предел
![]() .
.
Итак, данный ряд сходится и его сумма равна единице.
Основные свойства сходящихся рядов
Если ряд
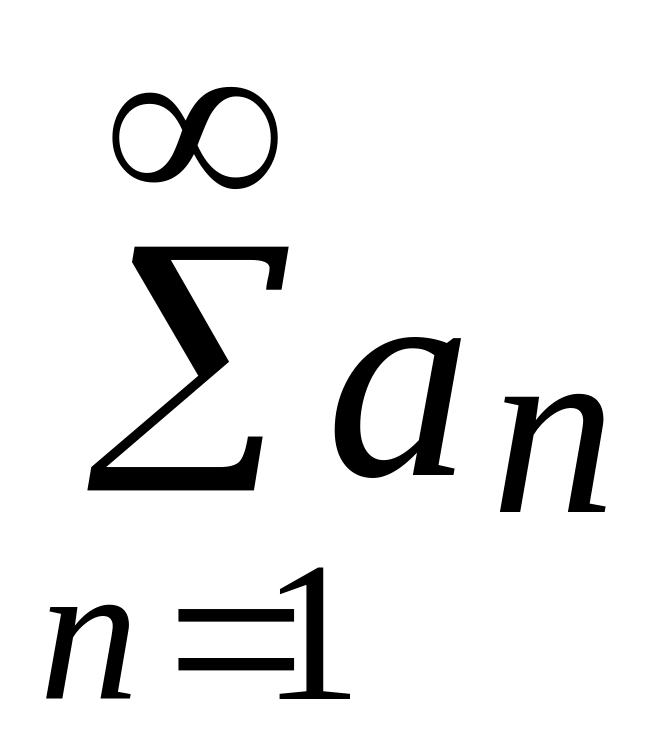 сходится,
то сходится и ряд, полученный отбрасыванием
из него любого конечного числа членов.
сходится,
то сходится и ряд, полученный отбрасыванием
из него любого конечного числа членов.Пусть даны ряды
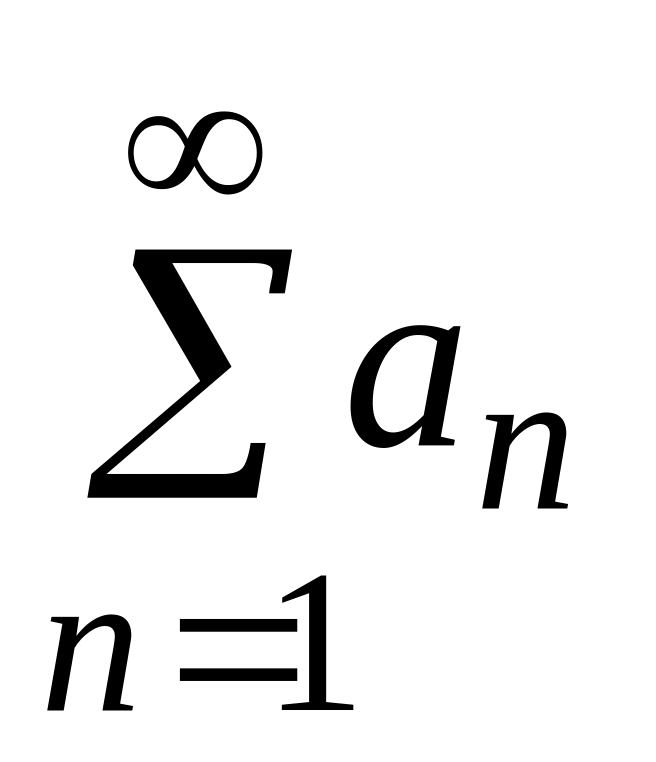 ,
,
 и
и
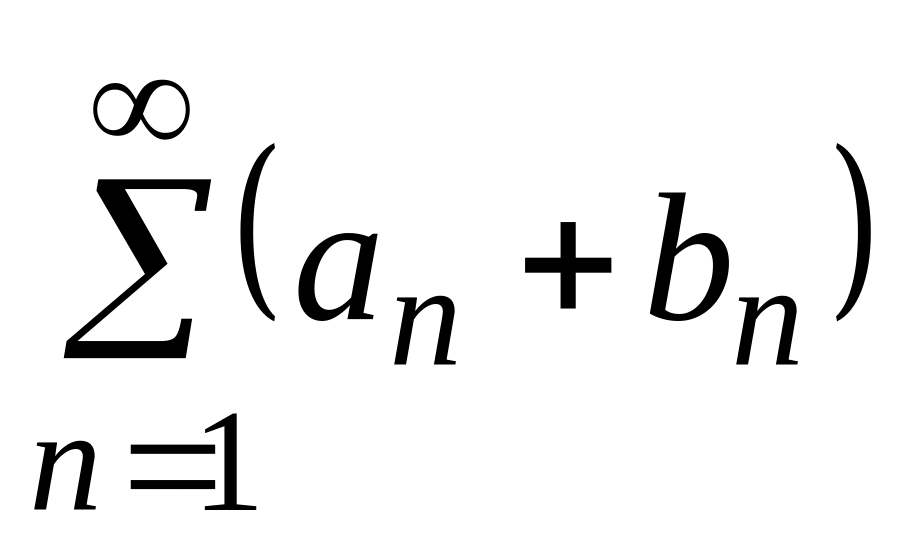 .
Если оба ряда
и
сходятся, а их суммы соответственно
равны
и
.
Если оба ряда
и
сходятся, а их суммы соответственно
равны
и
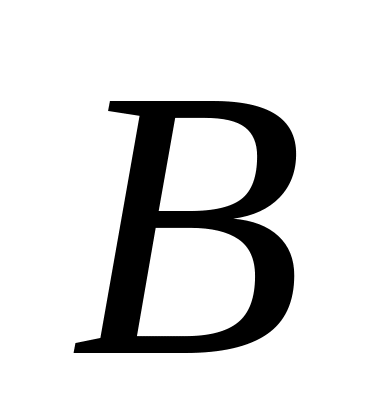 ,
то сходится и ряд
,
причем его сумма равна
,
то сходится и ряд
,
причем его сумма равна
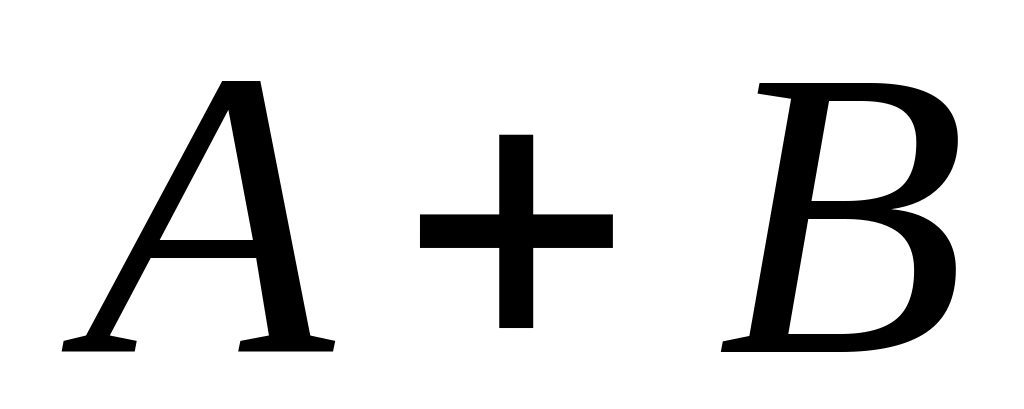 .
.Если ряд сходится и имеет сумму , то сходится и ряд
 ,
причем его сумма равна числу
,
причем его сумма равна числу
 ,
где
,
где
 .
.Если ряд сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, не изменяющей порядок расположения членов ряда, и суммы этих рядов одинаковы. К примеру, если сходится и его сумма равна , то ряд
![]()
также сходится, и его сумма равна .
Признаки сходимости числовых рядов
На практике часто не столь важно найти сумму ряда, как ответить на вопрос о сходимости ряда. Для этой цели используются признаки сходимости, основанные на свойствах общего члена ряда.
Необходимый признак сходимости ряда
Если
ряд
![]() сходится, то его общий член
стремится к нулю при
,
т.е.
сходится, то его общий член
стремится к нулю при
,
т.е.
![]() .
.
Кратко: если ряд сходится, то его общий член стремится к нулю.
Отсюда вытекает достаточный признак расходимости ряда.
Если , то ряд расходится.
Пример
4.
Исследовать
на сходимость ряд
![]()
Для
этого ряда общий член
![]() и
и
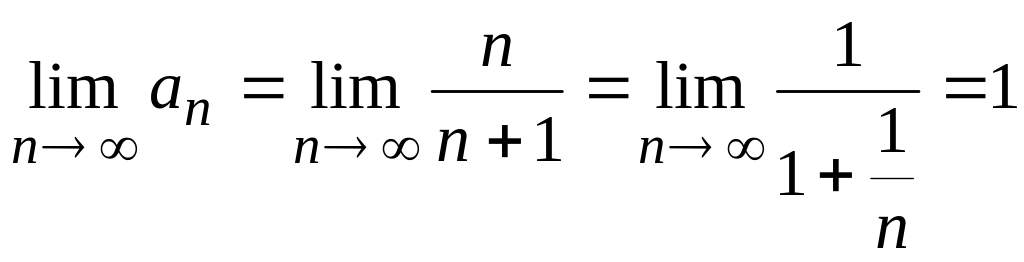 .
.
Следовательно, данный ряд расходится.
Пример
5.
Исследовать
на сходимость ряд
![]()
Очевидно,
что общий член этого ряда, вид которого
не указан ввиду громоздкости выражения,
стремится к нулю при
,
т.е. необходимый признак сходимости
ряда выполняется, однако этот ряд
расходится, так как его сумма
![]() стремится к бесконечности.
стремится к бесконечности.
