
- •20. Центральная предельная теорема
- •42.Проверка гипотеза о зависимости (независимости) случайных величин
- •41. Проверка гипотеза о зависимости (независимости) случайных величин
- •2.Билет
- •4Билет Формула полной вероятности
- •7Законы распределения дискретных случайных величин
- •8Распределение непрерывных случайных величин
- •9Системы случайных величин
- •10Условные законы распределения случайных величин, входящих в систему
- •12Нормальный закон на плоскости. Уравнение линии регрессии
- •13Функции от случайных аргументов
- •14 Билет
- •15Закон распределения функции от случайного аргумента общего вида
- •16Законы распределения функции от произвольного числа случайных аргументов
- •17Предельные теоремы теории вероятностей
- •18Частная теорема Чебышева
- •19Теорема Бернулли и Пуассона
15Закон распределения функции от случайного аргумента общего вида
Пусть задана
случайная величина Х
и известна её плотность распределения
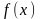 ,
задана функция от этой случайной
величины:
,
задана функция от этой случайной
величины:
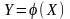
При этом во всей
области возможных значений х
имеется обратная функция:
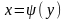 ,
а функция Y
– это функция общего вида, т.е. в области
возможных значений изменения х
есть интервалы возрастания и убывания
функции Y,
т.е. её можно представить в виде:
,
а функция Y
– это функция общего вида, т.е. в области
возможных значений изменения х
есть интервалы возрастания и убывания
функции Y,
т.е. её можно представить в виде:


Здесь рассматривается вероятность двух несовместных событий, т.е. вероятностей того, что Х попадёт в интервал (а, ψ1(y)), потом вероятность того, что Х(ψ2(y), ψ2(y)), далее Х(ψ4(y), ψn-1(y)) и т.д. Или:
Функция распределения случайной величины Х равна вероятности того, что Х попадёт в один из интервалов:
 (1)
(1)
Выражение (1) также можно записать в виде:
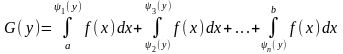 (2)
(2)
Формула (2) – это способ распределения случайной величины Y.
Для определения плотности распределения случайной величины Y необходимо взять производную от выражения (2) по правилу дифференцирования интеграла по двум переменным предела, а именно: производная от интеграла по двум переменным предела (по верхнему – убывающая часть графика – и нижнему) равна производной по верхнему пределу интеграла минус производную по нижнему пределу:
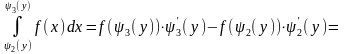

С учётом этого положения плотность распределения случайной величины Y (произвольной функции от случайного аргумента) будет определяться формулой:
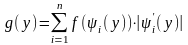 (3)
Где
(3)
Где
 - это число пересечений функции линией,
соответствующеё значению y:
- это число пересечений функции линией,
соответствующеё значению y:

16Законы распределения функции от произвольного числа случайных аргументов
Пусть задана система
случайных величин Х,
Y
с известной плотностью распределения
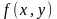 ,
также задана некоторая функция от
случайных аргументов:
,
также задана некоторая функция от
случайных аргументов:
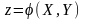 .Требуется
определить функцию распределения
случайной величины
.Требуется
определить функцию распределения
случайной величины
 и плотность её распределения
и плотность её распределения
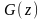 и
и
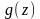 .
.
Представим функцию в виде некоторой поверхности:

Если сделать сечение этой поверхности плоскостью, параллельной плоскости xOy, на некоторой высоте , то область D будет ограничена линией уровня, которая представляет собой линию сечения поверхности данной плоскостью.
При известной плотности распределения системы функцию распределения величины можно представить в виде:
 (1)
(1)
Т.е. функцию распределения величины равняется вероятности того, что случайная точка (x, y) попадёт в область D.
17Предельные теоремы теории вероятностей
Ранее отмечалось, что теория вероятностей изучает закономерности массовых случайных явлений. Эти закономерности отражают устойчивость массовых случайных явлений. В широком смысле под устойчивостью понимается то, что при очень большом числе случайных явлений средний результат перестаёт быть случайным. В узком смысле под устойчивостью понимается ряд, в каждом из которых устанавливается факт приближения степени результатов опыта к некоторым определённым постоянным.
Другая группа теорем устанавливает условия, при которых наступает определённый закон распределения случайной величины.
Неравенство Чебышева
Неравенство Чебышева
утверждает: каково бы ни было положительное
число ,
вероятность того, что случайная величина
Х
отклонится от математического ожидания
на величину, большую или равную этому
числу (числу ),
ограничена сверху величиной
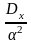 ,
т.е. справедливо неравенство:
,
т.е. справедливо неравенство:
 (1)
(1)
где
 - математическое ожидание случайной
величины;
- дисперсия.
- математическое ожидание случайной
величины;
- дисперсия.
Доказательство: Приведём доказательство этого неравенства для дискретной случайной величины (оно здесь более наглядно). Представим дискретную случайную величину в виде точек на числовой оси:

На этой оси отложим точку, соответствующую математическому ожиданию, относительно которой отложим отрезки - и . Известно, что дисперсия дискретной случайной величины:
 (2)
(2)
Наряду с выражением (2) рассмотрим две суммы:
 (3)
(3)
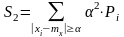 (4)
(4)
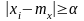 - это точки лежащие
правее/левее отрезков -
и .
- это точки лежащие
правее/левее отрезков -
и .
Из выражений (2),
(3) и (4) можно записать систему неравенств:
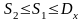 (5)
(5)
Выражение (4) можно
представить в виде:
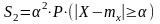 (6)
(6)
Тогда можно записать
неравенство в виде:
 (7)
(7)
Отсюда следует:
Аналогичным образом это неравенство можно доказать и для непрерывной случайной величины.
