Лекция № 13. Комбинаторика.

В этой лекции даются основные начальные сведения из комбинаторики. Это служебный раздел математики, занимающийся исследованием различных комбинаций элементов всевозможных множеств. Формулы комбинаторики широко используются теории вероятностей, в теории вычислительных машин, в некоторых разделах экономике, в статистике и других прикладных дисциплинах.

1. Правила суммы и произведения.

Будем в дальнейшем оперировать только с множествами, содержащими конечное число элементов. На бесконечные множества все нижеприведённые правила и формулы не распространяются.

Теорема 13.1.Пусть даны непересекающиеся конечные множества. Тогда мощность объединения этих множеств равна сумме мощностей данных множеств:

.

Доказательство этой теоремы очевидно. Но для нас представляет интерес другая интерпретация этой теоремы, которую мы сформулируем для двух множеств.

Если некоторый элемент можно выбратьспособами, а элемент-способами, причём любой способ выбора элементаотличается от любого способа выбора элемента, то выбор “или” можно сделатьспособами. Это правило называетсяправилом суммы.

Пусть даны непересекающиеся конечные множества . Обозначим число элементов в этих множествах (их мощности). Рассмотрим декартово произведение этих множеств. Напомним, что элементами этого произведения будут векторы (кортежи) длинывида.

Теорема 13.2.Число элементов в декартовом произведении множествравно произведению мощностей этих множеств:

.

Как и в предыдущем случае, сформулируем данную теорему упрощённым образом для двух множеств. Если элемент можно выбратьспособами, а элемент-способами, причём любой способ выбора элементаотличается от любого способа выбора элемента, то выбор “и” (то есть, пары) можно сделатьспособами. Это правило называетсяправилом произведения, илиумножения.

Оба сформулированных правила верны для любого конечного числа конечных множеств, и, в соответствующей форме, называются обобщёнными.

Пример 1.

а) В некоторой средней школе имеется три пятых класса, в которых обучаются соответственно 28, 31 и 26 учащихся. Требуется одного из них выбрать для участия в совете школы. Сколькими способами можно сделать выбор?

По правилу суммы получаем .

б) В секции фигурного катания занимаются 14 мальчиков и 18 девочек. Сколькими различными способами из детей, занимающихся в секции, можно образовать спортивные пары.

По правилу произведения получаем .

2. Размещения.

Определение.Любой вектор длины, составленный из элементовэлементного множества, в котором все элементы различны, называетсяразмещением без повторений по элементов из.Число всех размещений без повторений поэлементов изобозначаетсяи равно.

Пример 2.Куплено различных 12 книг. На полке можно поставить в ряд ровно 6 книг. Сколькими различными способами можно это сделать?

Будем считать различными не только те случаи, когда берутся разные книги, но и когда они по-разному расставлены на полке (в различном порядке). Тогда речь идёт о перестановках по 6 из 12. Получаем: .

Рассмотрим существенно другой случай, а именно когда элементы множества в векторах могут повторяться.

Определение.Любой вектор длины, составленный из элементовэлементного множества, состоящего изэлементов, в котором все элементы различны, называетсяразмещением с повторениями по элементов из.Число всех размещений с повторениями поэлементов изобозначаетсяи равно.

Пример 3. Сколько различных комбинаций может получиться при одновременном бросании трёх игральных костей?

Каждая игральная кость представляет собой кубик, на гранях которого нанесено от одного до 6 очков. При каждом бросании мы будем получать наборы вида , где- количество очков, выпавших на соответствующей кости. Речь идёт о перестановках с повторениями по 3 элемента из 6. Получаем:.

Замечание.Очевидно, что размещения без повторений являются частным случаем размещений с повторениями.

3. Перестановки.

Определение. Любой вектор длины, составленный из элементовэлементного множества, в котором все элементы различны, называетсяперестановкой без повторений из элементов.Число всех перестановок без повторений изэлементов обозначаетсяи равно.

Из определения и формулы видно, что перестановки без повторений есть частный случай размещений без повторений, при условии .

Пример 4.Сколькими различными способами можно расставить на полке 10 различных книг?

Здесь, в отличие от примера 2, значение имеет только порядок расставляемых книг. Поэтому речь идёт о перестановках из 10 элементов. Получаем: .

Рассмотрим случай, когда элементы множества повторяются по нескольку раз. Для определённости пусть 1-й элемент повторяетсяраз, 2-й элемент -раз и так далее. Тогда векторы длины, образованные из элементов данного множества называютсяперестановками из элементов с повторениями. Число таких перестановок обозначаетсяи равно.

Положив в последней формуле , получим формулу для перестановок без повторений.

Пример 5.Сколько различных шестизначных чисел могут быть записано с помощью цифр 1, 2, 2, 2, 3, 3?

Имеется набор из шести цифр, в котором цифра 2 повторяется трижды и цифра 3 – дважды. Полученные числа будут представлять собой перестановки с повторениями из 6 элементов. Получаем: .

4. Сочетания. Бином Ньютона.

Прежде всего, отметим одно существенное отличие перестановок от размещений. Если в размещениях векторы различаются и по составу элементов, и по их расположению (порядку) в наборе, то в перестановках векторы различаются только по расположению элементов. Естественно рассмотреть случай, когда векторы, наоборот, будут различаться только по составу элементов.

Определение.Любые различные векторы длины, составленные из элементовэлементного множества, различающиеся между собой по набору элементов, но не по их расположению в наборе, называются сочетаниями поэлементов из.

Если все элементы, образующие сочетания, различны, то их называют сочетанием без повторений. Обозначение всех сочетаний без повторений. Формула для вычисления. Если некоторые (или все) элементы, образующие сочетания, могут повторяться, то их называютсочетаниями повторениями. Обозначение всех сочетаний без повторений. Формула для вычисления. Запоминать последнюю формулу нет необходимости.

Замечание 1.Сочетания являются частным случаем размещений. Разница между сочетаниями и размещениями из определения неочевидна, но на конкретных примерах её легко видеть. Так, например, векторыиявляются различными размещениями, но обозначают одно и то же сочетание.

Замечание 2. Для сочетаний без повторений обязательно требование, причём в случае равенства получим естественный результат. Но для сочетаний с повторениями это требование необязательно, как будет видно из приведённого ниже примера.

Пример 6.

а) В отделе работают 10 сотрудников. Требуется отобрать трёх из них для того, чтобы направить в командировку. Сколькими способами можно это сделать?

Поскольку имеет значение только то, какие именно сотрудники отобраны, то речь идёт о сочетаниях без повторений по 3 элемента из 10. Получаем:

б) В цветочном магазине имеются в продаже 5 различных видов цветов. Покупателю требуется составить букет из 7 цветов. Сколькими способами можно это сделать?

Будем считать различными те букеты, которые отличаются друг от друга по подбору цветов. Поскольку цветы в букете могут повторяться, то речь идёт о сочетаниях с повторениями по 7 элементов из 5. Тогда получим .

Одним из наиболее известных примеров использования комбинаторных формул является так называемый бином Ньютона. В общем виде формула бинома (двучлена) Ньютона выглядит так:

.

С частными случаями применения этой формулы ( для случаев и) сталкиваются ещё в школе при изучении формул сокращённого умножения:

.

На практике для удобства применении бинома Ньютона применяют так называемый треугольник Паскаля, который содержит числовые коэффициенты полинома в правой части формулы:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…………………..

Назад, в начало конспекта.

РАЗДЕЛ IV. ТЕОРИЯ ГРАФОВ.

Лекция № 14. Графы: основные понятия и операции.

Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В дальнейшем оказалось, что понятие графа можно применять не только при исследовании геометрических конфигураций. Особенно часто определяют графы при анализе функционирование неких систем.

1. Графы, их вершины, рёбра и дуги. Изображение графов.

Определение.Если на плоскости задать конечное множествоVточек и конечный набор линийE, соединяющих некоторые пары из точекV, то полученная совокупность точек и линий будет называтьсяграфом G = (V, E).

При этом элементы множества Vназываютсявершинамиграфа, а элементы множестваE–ребрами.

Определение.Если вершинаvявляется концом ребра, то говорят, чтоvи инцидентны.

В множестве Vмогут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называютсяпетлями(на рисунке 1.4 при вершине 5 имеется петля). Одинаковые пары в множествеEназываютсякратными(или параллельными) ребрами. Количество одинаковых пар(v, w)вEназываетсякратностью ребра (v,w). Например, на рисунке 1.1 все рёбра имеют кратность 1, а на рисунке 1.2 есть два ребра, соединяющих одни и те же вершины 1 и 4, следовательно, их кратность равна двум.

Множество Vи наборEопределяют граф с кратными ребрами –псевдограф.

Псевдограф без петель называется мультиграфом.

Если в наборе Eни одна пара не встречается более одного раза, то мультиграф называетсяграфом.

Ниже, на рисунке 1.1 изображен граф, на рисунке 1.2 мультиграф, на рисунке 1.4 – псевдограф.

Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины. На рисунке 1 изображены некоторые неориентированные графы.

Рисунок 1.

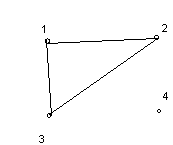
1.1 1.2 1.3

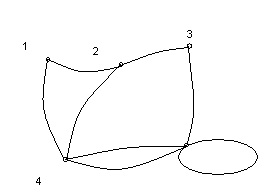
1.4 1.5

Замечание 1.Слово “линия”, которое мы используем, подразумевает несущественность того, какая конкретно линия используется для соединения двух вершин графа, то есть её геометрические характеристики не имеют значения.

Замечание 2.Граф можно определить, также как совокупность двух множестви, между элементами которых установлено отношение инцидентности, при котором каждый элементинцидентен ровно двум элементам.

Определение.Еслих= {v, w} – ребро графа, то вершиныv, wназываются концами ребрах.

Определение.Если пары в набореEявляются упорядоченными, то граф называется ориентированным илиорграфом.

Если пишут = (v, w)– дуга орграфа, то вершинаv– начало, а вершинаw– конец дугих.

Определение.Вершиныv, w графаG= (V,E) называютсясмежными, если {v,w}Е. Два ребра называютсясмежными, если они имеют общую вершину.

Определение. Степеньювершины графа называется число ребер, которым эта вершина принадлежит. Вершина называетсявисячей, если ее степень равна единице иизолированной, если ее степень равна нулю.

На рисунке 1.5 все вершины, кроме вершины 1, являются висячими. На рисунке 1.3 вершина 4 является изолированной. Если граф состоит только из таких вершин, его называют пустым.В некоторых случаях пустым называют граф, не имеющей ни одной вершины.

Рисунок 2.

2.1 2.2 2.3

1. 2.5

На рисунке 2 представлены различные типы ориентированных графов.

Заметим, что каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя противоположными рёбрами, инцидентными тем же вершинам. Такое соответствие называется каноническим.

2. Матрица инцидентности и список рёбер. Матрица смежности графа.

Обычно рассматриваемые графы конечны, то есть, конечны множества их элементов – вершин и рёбер. Поэтому в дальнейшем конечность графов не будет оговариваться, тем более, что важнейшие понятия и результаты, приводимые ниже относятся к произвольным графам.

Задать граф – значит, описать множества его вершин и рёбер и задать между ними отношение инцидентности. Когда граф конечный, для описания его вершин и рёбер достаточно их занумеровать. Пусть- вершины графа, а- его рёбра. Отношение инцидентности можно определить матрицейразмерности. Столбцы этой матрицы будут соответствовать вершинам графа, а строки – его рёбрам. Если реброинцидентно вершине, то, в противном случае -. Такая матрица называется матрицей инцидентности неориентированного графа, поскольку по способу её задания невозможно различить начало и конец каждого ребра.

Пример 1.Составить матрицу инцидентности неориентированного графа, изображённого на рисунке 3.

Рисунок 3.

Строим матрицу инцидентности в виде таблицы:

	1	2	3	4	5	6	7
a	1	1	0	0	0	0	0
b	1	0	1	0	0	0	0
c	0	1	0	1	0	0	0
d	1	0	0	0	1	0	0
e	0	1	0	0	0	1	0
f	0	0	1	1	0	0	0
g	0	0	1	0	1	0	0
h	0	0	0	1	0	1	0
i	0	0	0	0	1	0	1
j	0	0	0	0	0	1	1

Для ориентированного графа матрица инцидентности составляется иначе. Это матрица размерности.

Если вершина - начало ребра, то. Если вершина- конец ребра, то. Если вершинеинцидентна петля, то, гделюбое число, кроме чисел(обычно берут 2). В любом противном случае -.

Пример 2. Построить матрицу инцидентности для графа, изображённого на рисунке 4.

Строим матрицу инцидентности в виде таблицы:

	1	2	3	4	5	6	7
a	-1	1	0	0	0	0	0
b	-1	0	1	0	0	0	0
c	0	-1	0	1	0	0	0
d	0	0	-1	0	1	0	0
e	0	0	-1	0	0	1	0
f	0	0	-1	0	0	0	1
g	0	0	0	0	0	0	2

Ещё проще задавать граф с помощью таблицы рёбер. Она состоит из двух столбцов; в левых содержатся названия рёбер, а в правых – инцидентные им вершины (для ориентированных графов обязательно сначала указывается начало ребра, потом конец). Ниже приведены таблицы рёбер для графов из примеров 1 и 2.

Для примера 1:

Рёбра	Вершины
a	1, 2
b	1, 3
c	2, 4
d	1, 5
e	2, 6
f	3, 4
g	3, 5
g	4, 6
i	5, 7
j	6, 8

Для примера 2:

Рёбра	Вершины
a	1, 2
b	1, 3
c	2, 4
d	3, 5
e	3, 6
f	3, 7
g	7, 7

Очевидно, по списку рёбер можно построить его таблицу инцидентности. Действительно, каждая строка этого списка соответствует строке матрицы с тем же номером; аналогично можно выполнить обратную процедуру.

Ещё одним способом представления графа является построение для него матрицы смежности. Это квадратная матрица , в которой количество строк и столбцов равно количеству вершин графа. Для неориентированного графаэта матрица определяется следующим образом. Если вершиныиявляются смежными, то есть если выполняется, то. В противном случае,. Для графа из примера 1 таблица смежности имеет вид:

	1	2	3	4	5	6	7
1	0	1	1	0	1	0	0
2	1	0	0	1	0	1	0
3	1	0	0	1	1	0	0
4	0	1	1	0	0	1	0
5	1	0	1	0	0	0	1
6	0	1	0	1	0	0	1
7	0	0	0	0	1	1	0

Матрица смежности неориентированного графа обязательно симметрична. Размерность матрицы указывает на количество вершин, а число рёбер равно половине единиц, имеющихся в матрице.

Матрица смежности ориентированного графа отличается только тем, что в том и только в том случае, когда в паре смежных вершинивершинаявляется началом, а вершина- концом ребра. Для графа из примера 2 матрица смежности выглядит следующим образом:

	1	2	3	4	5	6	7
1	0	1	1	0	0	0	0
2	0	0	0	1	0	0	0
3	0	0	0	0	1	1	1
4	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0
6	0	0	0	0	0	0	0
7	0	0	0	0	0	0	1

Очевидно, что вся информация об ориентированном графе, порождающем некоторую матрицу смежности, содержится в верхнем (относительно главной диагонали) её треугольнике.

Ориентированный граф с симметричной матрицей смежности канонически соответствует неориентированному графу, имеющему ту же таблицу смежности (но не наоборот).

3. Идентификация графов, заданных своими представлениями.

Итак, граф может быть представлен различными способами. Он может быть задан рисунком, матрицей инцидентности, списком рёбер или матрицей смежности. Вид чертежа зависит от формы линий и взаимного расположения вершин. Иногда, даже для пары достаточно простых графов, непонятно, одинаковы ли они (см. рисунок 5 “а” и “б”). Вид матриц, также как списков рёбер зависит от нумерации вершин и рёбер графа. В связи с этим возникает весьма существенный вопрос о том, как определять равенство графов.

Рисунок 5.

а) б)

Строго говоря, граф считается полностью заданным, если нумерация его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, называютсяизоморфными.

Определение. ГрафыG₁(V₁, E₁)иG₂(V₂, E₂)называютсяизоморфными, если существует взаимно однозначное отображение: V₁  V₂, сохраняющее смежность.

Перенумерация вершин графа задаётся строкой новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается из исходной матрицы перемещением каждого элементавстроку, встолбец. Поэтому, чтобы узнать, представляют ли две таблицы смежности изоморфные графы, можно, например, перевести всевозможные одинаковые перестановки строк и столбцов первой матрицы. Если одна из таких перестановок даст матрицу, тожественно совпадающую со второй матрицей, то представляемые ими графы изоморфны. Однако эта процедура может оказаться очень трудоёмкой, так как всего возможно выполнениеперестановок.

Назад, в начало конспекта.