Курсовая работа - Задача о максимальном потоке / инфа о фф

Алгоритм Форда-Фалкерсона.

Впервые был предложен в 1956г. До этого времени задача решалась с помощью методов линейного программирования, что было крайне не эффективно. Алгоритм является псевдополиномиальным и имеет оценку O(nm log U), где m = |E|, n = |V|, U = max(C_ij).

Алгоритм начинает свою работу с нулевого потока и на каждой своей итерации увеличивает поток в сети. На каждом шаге находится увеличивающая величину потока цепь. Поток увеличивается вдоль дуг этой цепи, пока она не станет насыщенной.

Увеличивающей цепью является цепь из источника в сток, все дуги которой допустимы. Дугу из вершины a в вершину b назовем допустимой, если выполняется одно из следующих условий:

1.      f(e) < c(e) и дуга согласованна

2.      f(e) > 0 и дуга несогласованна

По увеличивающей цепи можно пустить поток величины Q, где Q = min{q(e_i), 1 ≤ i ≤ l} и q(e) = {с(e) – f(e), если дуга согласованна, f(e), если дуга не согласованна}. Для того, чтобы увеличить величину потока сети на Q, необходимо увеличить на Q поток на каждой согласованной дуге цепи и уменьшить на каждой несогласованной.

В своей работе [3] Форд и Фалкерсон (Ford and Fulkerson) доказали, что поток в сети, для которой нельзя построить увеличивающую цепь, является максимальным.

Для нахождения увеличивающей цепи ими был предложен “Метод расстановки пометок”. Процесс расстановки меток начинается в источнике сети и заканчивается в ее стоке. Как только сток оказался помеченным, мы можем говорить о существовании увеличивающей цепи из источника в сток. Метка, “наносимая” на вершины сети, содержит необходимый минимум информации, достаточный для того, чтобы восстановить эту цепь и определить величину, на которую можно изменить поток в ней. Вершина сети может находиться в одном из 3-х состояний: “непомеченная”, “помеченная” и “просмотренная”.

Этап 1. Расстановка меток.

Все вершины получают статус непомеченных.

Процедура расстановки меток.

Возьмем произвольный помеченный, но не просмотренный узел x. Пусть он имеет пометку [i, +, e(x)], где i – вершина из которой был помечен x; флаг, показывающий, что дуга (i,x) согласованна; e – величина потока, который можно пропустить по этой дуге. Рассмотрим все непомеченные смежные вершины y, такие что дуга (x, y) согласованна. Пометим вершину y меткой [x, +, e(y)], где e(y) = min{e(x) , c(x, y) – f(x, y)}. Затем рассмотрим все непомеченные смежные вершины y, соединенные с ней несогласованной дугой. Пометим их меткой [x, -, e(y)], где e(y) = min{e(x), f(y,x)}. Теперь все рассмотренные узлы y имеют статус помеченных, а узел x - просмотренный.

Эта общая для всех узлов сети процедура. Пометим источник меткой [~, ~, ∞] и будем последовательно вызывать ее для всех смежных узлов, постепенно двигаясь по сети. Как только процедура будет вызвана для стока, будет получена увеличивающая цепь и следует перейти ко второму этапу. В противном случае процедура будет вызываться, пока все помеченные вершины не станут просмотренными, и если сток сети не был достигнут – увеличивающая цепь не может быть построена и по теореме Форда-Фалкерсона имеющийся поток сети является максимальным.

Этап 2. Изменение потока.

Процедура изменения потока дуги.

Возьмем узел x. Если он имеет метку [y, +, e], то увеличим поток по дуге (y, x) на e. Если он имеет метку [y, -, e], то уменьшим поток по дуге (y, x) на e. Если y не является источником, то вызовем процедуру для узла y.

Эта процедура, будучи вызвана для стока сети, позволяет пройти по найденной увеличивающей цепи к стоку, изменяя поток на ее дугах.

Следует особо отметить, что узлы, имеющие статус “помеченных”, больше не участвуют в процессе поиска увеличивающей цепи, весьма эффективно с вычислительной точки зрения.¹[1]

Алгоритм Форда-Фалкерсона гарантирует нахождение максимального потока только в сетях с целочисленными пропускными способностями. На практике “чистый” алгоритм Форда-Фалкерсона не применяется, т.к. оценка его производительности зависит от величины пропускных способностей дуг сети. Все дело в том, что в нем не дается каких либо правил выбора увеличивающей цепи.

Рассмотрим сеть на рис. 1. Предположим, что реализован алгоритм, отдающий предпочтение увеличивающим цепям максимальной длины. В этом случае на первом шаге мы пустим дополнительный поток по цепи (0,1),(1,2),(2,3).

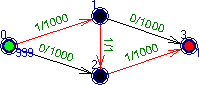
рис. 1 рис. 2

На втором шаге выберем цепь (0,2),(2,1),(1,3). Так как дуга (2,1) несогласованна, величина пущенного по ней потока будет вычитаться из величины потока, полученного на предыдущем шаге. Мы получили сеть (рис. 3) практически эквивалентную исходной.

рис. 3

Очевидно, что для нахождения максимального потока понадобиться 1000 итераций! В то время, как если бы мы на первом шаге выбрали цепь (0,1),(1,3), то результат был бы получен за одну итерацию! На практике, величина пропускных способностей часто зависит от единиц измерения, и может принимать огромные значения. Если же допустить иррациональные пропускные способности дуг, то можно привести пример невычислимой сети [4]. Величина потока в такой сети не превысит даже четверти истинного значения. Подобная неопределенность длилась не долго, уже в начале 70-х г. были предложены сразу 2 правила выбора увеличивающих цепей, которые существенно улучшают алгоритм Форда-Фалкерсона.

Рассмотрим ориентированный граф. Будем рассматривать его как сеть труб, по которым некоторое вещество движется от истока (где оно производится с постоянной скоростью) к стоку (где оно потребляется — с той же скоростью). Вместо потоков вещества можно рассматривать движение тока по проводам, деталей по конвейеру, информации по линиям связи или товаров от производителя к потребителю.

Как и в задаче о кратчайших путях, на каждом ребре графа мы пишем число. Но если раньше это число означало длину пути, то теперь это скорее ширина дороги, или пропускная способность трубы — максимальная скорость потока в этой трубе.

Мы считаем, что в вершинах вещество не накапливается — сколько приходит, столько и уходит (если вершина не является истоком или стоком).

Задача о максимальном потоке для данной сети состоит в следующем: найти максимально возможную скорость производства (и потребления) вещества, при которой его еще можно доставить от истока к стоку при данных пропускных способностях труб.

В данной статье описывается классический метод решения этой задачи — метод Форда-Фалкерсона. Мы не говорим об алгоритме поскольку есть несколько алгоритмов, реализующих этот метод; они отличаются временем работы. Одна из таких реализаций и приведена здесь — алгоритм Эдмондса-Карпа.

Ключевую роль в методе Форда-Фалкерсона играют два понятия: остаточные сети и дополняющие пути.

Поиск максимального потока данным методом проводится по шагам. Вначале поток нулевой (и величина его равна нулю). На каждом шагу мы увеличиваем значение потока. Для этого мы находим "дополняющий путь", по которому можно пропустить ещё немного вещества, и используем его для увеличения потока. Этот шаг повторяется, пока есть дополняющие пути. Как следует из теории, полученный поток будет максимальным.

Остаточные сети

Пусть дана сеть и поток в ней. Тогда остаточная сеть состоит из тех ребер (называемых также остаточными), поток по которым можно увеличить. Заметим, что остаточное ребро не обязано быть ребром исходной сети. Такие "странные" ребра появляются когда имеется поток вещества в обратном направлении — ведь этот поток можно уменьшить.

У остаточных сетей есть интересное свойство — если в остаточной сети существует поток f, то прибавив его к исходному потоку в сети, мы получим также поток, удовлетворяющий всем требованиям, но который больше исходного.

Дополняющие пути

Назовем дополняющим путем простой путь из истока в сток в остаточной сети. Из определения остаточной сети вытекает, что по всем ребрам дополняющего пути можно переслать ещё сколько-то вещества, не превысив их пропускную способность. Величину наибольшего потока, который можно переслать по дополняющему пути назовем остаточной пропускной способностью пути. Очевидно, она равна значению минимального остаточного ребра, входящего в данный путь.

Общая схема метода Форда-Фалкерсона

Действуя по нашему методу, на каждом шаге мы выбираем произвольный дополняющий путь и увеличиваем поток, добавляя поток величины остаточной пропускной способности вдоль выбранного пути.

Время работы алгоритма зависит от того, как ищется дополняющий путь. Логично было бы искать его методом поиска в ширину, в этом случае путь будет кратчайшим из всех дополняющих путей(если длину каждого ребра считать единицей). Эта реализация метода Форда-Фалкерсона называется алгоритмом Эдмондса-Карпа. Время его работы есть O(V*E2).

К задаче о максимальном потоке в сети сводятся некоторые комбинаторные задачи — например задача о максимальном паросочетании в двудольном графе (см. соотв. визуализатор).

Чтобы решить эту задачу, добавляем к имеющемуся графу две вершины, одна из которых будет истоком, а вторая — стоком и соединяем соотв. исток с каждой вершиной одной доли, а сток — с каждой вершиной другой. При этом все пропускные способности ставим одинаковые — например по 1, а все ребра превращаем в дуги, направленные от истока к стоку. Если найти в получившейся сети максимальный поток, тогда величина его будет равна мощности максимального паросочетания, а дуги, по которым будет течь этот максимальный поток и будут насыщенными ребрами максимального паросочетания.

Алгоритм Форда-Фалкерсона. Поток в сети.

Определение 1:

          Сетью называется связный орграф без петель.

Определение 2:

          Потоком в сети называется некоторая функция, которая ставит в соответствие дуге некоторое число-вес дуги.

Для определения потока в сети используют алгоритм Форда-Фалкерсона:

а) ищем любую цепь из истока графа в сток;

б) каждой дуге приписываем возможный больший поток из истока в сток (записываем его через дробь с весом дуги; при этом поток не может превысить вес дуги, но может быть ему равен);

в) если поток становится равен весу дуги, то эта дуга является насыщенной, то есть через нее нельзя пройти при рассмотрении цепей в графе;

г) так перебираем все возможные цепи, пока станет невозможно попасть из истока в сток;

д) поток  в сети будет равен сумме потоков всех дуг, инцидентных стоку графа (следует заметить, что сумма потоков всех дуг, инцидентных стоку графа равна сумме потоков всех дуг, инцидентных истоку графа).

Задача 9.17

Дана сеть. Определить поток в сети.

Решение:

Следуя вышеописанному алгоритму, рассмотрим следующие цепи:

1-5-9-13-14;

1-4-8-12-14;

1-3-7-11-14;

1-2-6-10-14

Расставив потоки у соответствующих дуг, получим:

Далее будем выбирать цепи так, чтобы насыщались дуги, инцидентные истоку.

1-4-9-13-12-14 (здесь поток каждой дуги увеличивается на единицу);

1-4-9-8-13-12-14 (здесь также на единицу);

1-4-9-8-13-12-11-14 (и здесь тоже на единицу).

После этой последовательности цепей получим насыщенную дугу 1-4.

 

Следующая последовательность цепей дает нам окончательный результат:

1-3-4-9-8-13-12-11-14 (здесь поток каждой дуги увеличивается на двойку);

1-2-3-4-9-8-13-12-11-14 (здесь поток каждой дуги опять увеличивается на двойку).

Поток в сети равен 4+9+7+6=6+6+8+6=26.

Насыщенные дуги: 1-4,1-3,1-2, 5-9, 9-13, 13-14, 13-12, 4-8, 8-12, 12-14, 3-7, 11-14, 2-6, 3-4.

Программа к задаче:

> restart:with(networks):

> new(G):V:=$1..14:addvertex([V],G):

> v1:=1:#источник

> v2:=14:#сток

> E:=[[1,5],[1,4],[1,3],[1,2],[2,3],[2,6],[3,4],[3,7],[4,8],[4,9],[4,5],[5,9],[6,10],[6,3],[7,4],[7,11],[7,6],[8,7],[8,12],[8,13],[9,13],[9,8],[10,14],[10,7],[11,10],[11,8],[11,14],[12,14],[12,11],[13,12],[13,14]]:

> w:=[9,8,6,6,3,4,4,4,5,10,3,6,5,9,10,5,8,8,5,12,7,7,6,10,8,12,9,7,8,7,6]:

> addedge(E,weights=w,G):

> potok=flow(G,v1,v2,ed);

Аннотация

Дан граф, ребра — это трубы, вершины — это соединения труб. Для каждого ребра (трубы) указана проводимость. Две вершины в графе помечены как исток A и выход B. Нужно найти максимальную проводимость этой сети труб — максимальный поток из A в B. Эта задача решается за полиномиальное время. Два наиболее популярных алгоритма — алгоритм Форда-Фалкерсона и алгоритм "проталкивания предпотока".

Формулировка задачи

Рассмотрим ориентированный граф , каждому ребру (u,v) которого поставлено в соответствие число называемое пропускной способностью ребра. Если не принадлежит графу, то положим . В графе выделим две вершины: исток — s, и сток — t. Такой граф назовем сетью(flow network). Потоком в сети G назовем функцию , обладающую следующими свойствами:

1. f(u,v) <= c(u,v).

2. f(u,v) = -f(v,u)

3. Закон сохранения жидкости: для каждой вершины (поток входящий) = (поток исходящий) за исключением стока и истока.

Определим величину потока, как сумму f(s, u) по всем вершинам u, т.е. суммарный поток по всем ребрам выходящим из истока.

Тогда возникает задача о максимальном потоке - какой может быть максимальная величина потока в данной сети?

Образно сеть и поток можно представить так: сеть - система труб проводящих жидкость, каждая труба проводит не белее определенного количества жидкости и только в одном направлении. Исток - источник жидкости, а сток приемник. Если открыть исток запустив в сеть жидкость, то она потечет по "трубам" - ребрам к истоку в соответствии с их пропускной способностью. Это собственно и будет потоком. А максимальный поток - величина характеризующая максимальное количество жидкости способное протекать по сети за единицу времени.

Метод Форда-Фалкерсона

Один из способов поиска максимального потока — метод Форда-Фалкерсона:

1. Положим начальный поток равным нулю.

2. Пока есть простой путь из истока в сток, по которому можно еще пустить поток, дополняем поток по этому пути.

Наиболее эффективной реализацией метода Форда-Фалкерсона является алгоритм Эдмондса-Карпа, суть которого состоит в том, что поиск пути выполняется обходом дерева в ширину. Для данного алгоритма получается оценка O(V*E*E);

Подробное описание алгоритмов поиска максимального потока  можно найти в книге "Алгоритмы. Построение и анализ" Т. Кормен, Ч. Лейзерсон, Р. Ривест ("Introduction to Algorithms" Thomas Cormen, Charles Leiserson, Roland Rivest) , стр. 536 - 573.

6

0 5

0 16 0 0 13 0

0 0 12 0 6 0

0 0 0 0 9 20

0 0 7 0 0 4

0 0 0 14 0 0

0 0 0 0 0 0

Результат: 23

#include <memory.h>

#include <stdio.h>

const int MAX_VERTICES = 40;

int NUM_VERTICES; // число вершин в графе

const int INFINITY = 10000; // условное число обозначающее бесконечность

// f - массив садержащий текушее значение потока

// f[i][j] - поток текущий от вершины i к j

int f[MAX_VERTICES][MAX_VERTICES];

// с - массив содержащий вместимоти ребер,

// т.е. c[i][j] - максимальная величину потока способная течь по ребру (i,j)

int c[MAX_VERTICES][MAX_VERTICES];

// набор вспомогательных переменных используемых функцией FindPath - обхода в ширину

// Flow - значение потока чарез данную вершину на данном шаге поиска

int Flow[MAX_VERTICES];

// Link используется для нахождения собственно пути

// Link[i] хранит номер предыдущей вешины на пути i -> исток

int Link[MAX_VERTICES];

int Queue[MAX_VERTICES]; // очередь

int QP, QC; // QP - указатель начала очереди и QC - число эл-тов в очереди

// поск пути по которому возможно пустить поток алгоритмом обхода графа в ширину

// функция ищет путь из истока в сток по которому еще можно пустить поток,

// считая вместимость ребера (i,j) равной c[i][j] - f[i][j],

// т.е. после каждой итерации(одна итерация - один поик пути) уменьшаем вместимости ребер,

// на величину пущеного потока

int FindPath(int source, int target) // source - исток, target - сток

{

QP = 0; QC = 1; Queue[0] = source;

Link[target] = -1; // особая метка для стока

int i;

int CurVertex;

memset(Flow, 0, sizeof(int)*NUM_VERTICES); // в начале из всех вершин кроме истока течет 0

Flow[source] = INFINITY; // а из истока может вытечь сколько угодно

while (Link[target] == -1 && QP < QC)

{

// смотрим какие вершины могут быть достигнуты из начала очереди

CurVertex = Queue[QP];

for (i=0; i<NUM_VERTICES; i++)

// проверяем можем ли мы пустить поток по ребру (CurVertex,i):

if ((c[CurVertex][i] - f[CurVertex][i])>0 && Flow[i] == 0)

{

// если можем, то добавляем i в конец очереди

Queue[QC] = i; QC++;

Link[i] = CurVertex; // указываем, что в i добрались из CurVertex

// и находим значение потока текущее через вершину i

if (c[CurVertex][i]-f[CurVertex][i] < Flow[CurVertex])

Flow[i] = c[CurVertex][i];

else

Flow[i] = Flow[CurVertex];

}

QP++;// прерходим к следующей в очереди вершине

}

// закончив поиск пути

if (Link[target] == -1) return 0; // мы или не находим путь и выходим

// или находим:

// тогда Flow[target] будет равен потоку который "дотек" по данному пути из истока в сток

// тогда изменяем значения массива f для данного пути на величину Flow[target]

CurVertex = target;

while (CurVertex != source) // путь из стока в исток мы восстанавливаем с помощбю массива Link

{

f[Link[CurVertex]][CurVertex] +=Flow[target];

CurVertex = Link[CurVertex];

}

return Flow[target]; // Возвращаем значение потока которое мы еще смогли "пустить" по графу

}

// основная функция поиска максимального потока

int MaxFlow(int source, int target) // source - исток, target - сток

{

// инициализируем переменные:

memset(f, 0, sizeof(int)*MAX_VERTICES*MAX_VERTICES); // по графу ничего не течет

int MaxFlow = 0; // начальное значение потока

int AddFlow;

do

{

// каждую итерацию ищем какй-либо простой путь из истока в сток

// и какой еще поток мажет быть пущен по этому пути

AddFlow = FindPath(source, target);

MaxFlow += AddFlow;

} while (AddFlow >0);// повторяем цикл пока поток увеличивается

return MaxFlow;

}

int main()

{

int source, target;

scanf("%d", &NUM_VERTICES);

scanf("%d %d", &source, &target);

int i, j;

for (i=0; i<NUM_VERTICES; i++)

for (j=0; j<NUM_VERTICES; j++)

scanf("%d",&c[i][j]);

printf("%d", MaxFlow(source, target));

return 0;

}

Сети и потоки в сетях. Стационарные потоки. Алгоритм Форда-Фалкерсона поиска максимального стационарного потока. (Данный вопрос лучше смотреть в сетевых моделях исследования операций).

Пусть - некоторый орграф и вещественно-значная функция на множестве ребер; тогда пара называется сетью, а функция в контексте сети называется функцией пропускной способности или пропускной способностью сети.

Всякая функция , удовлетворяющая неравенству , называется потоком в сети. В обсуждении свойств потоков в сети традиционно используется следующее обозначение:

пусть - любая функция и - два любых подмножества вершин; символ будет обозначать сумму значений функции на ребрах таких, что и ; если состоит из единственной вершины , то символ обозначает сумму весов ребер, начинающихся в и заканчивающихся в вершинах из ; аналогичный смысл имеет символ - сумма значений функции на ребрах, начинающихся в и заканчивающихся в вершине .

Поток в сети называется стационарным, если существуют две вершины и число такие, что выполнены следующие условия:

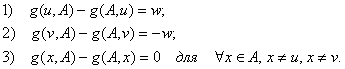
В этой ситуации число называется величиной потока , вершина называется источником, а вершина - стоком потока .

Известна следующая классическая задача о максимальном потоке: в данной сети для данного источника и для данного стока найти стационарный поток максимально возможной величины. Можно доказать, что такая задача всегда имеет решение. Один из способов ее ре- шения называется алгоритмом Форда-Фалкерсона. Сформулируем этот алгоритм по шагам.

Шаг 0. Фиксируем на данной сети с источником и стоком произвольный стационарный поток , например - поток, тождественно равный нулю (т.е. равный нулю на каждом ребре данного орграфа ). Нетрудно проверить, что такой поток действительно стационарный и имеет величину 0.

Шаг 1. Около вершины поставим пометку следующего вида:

.

Здесь символ обозначает число, заведомо превосходящее все числа, которые будут участвовать в дальнейших рассмотрениях (в случае программирования это - компьютерная бесконечность, т.е. самое большое число, допускаемое данным программным средством).

Замечание. Почти все дальнейшие действия по алгоритму представляют собой расстановку пометок около некоторых вершин. Цель этой расстановки в том, чтобы в конце концов поставить пометку у стока или установить, что сток пометить невозможно. В первом

случае окажется возможным заменить имеющийся стационарный поток на другой стационарный поток, имеющий величину, большую, чем величина потока . После этого надо будет запустить все сначала. Во втором случае окажется, что имеющийся поток оптимален, т.е. его величина имеет максимальное возможное значение. Каждая пометка, кроме уже проставленной около источника , будет иметь вид , где - некоторое число, а - имя одной из вер-шин орграфа , причем реально в пометке это имя будет либо в виде , либо в виде .

Шаг 2. Пусть - некоторое ребро, начало которого, т.е. вершина , уже имеет некоторую пометку (или, если - это источник , то пометку , где ). Ес-ли , т.е. поток равен на ребре пропускной способности , то пометка у вершины не проставляется. Если же , то пометка у вершины выставляется следующим образом.