2)Математическая модель задачи об использовании сырья

Пример1(задача о распределении ресурсов). В изготовлении двух видов продукции Р1 и Р2 используется сырьё видов S1,S2,S3 в количестве b1,b2,b3. Запасы сырья, идущего на изготовление единицы продукции, а также величина прибыли от реализации ед. продукции приведены в таблице.

запасы сырья	кол-во сырья на изг. 1 ед. продукции
	Р1	Р2
S1 b1 S2 b2 S3 b3	a11 a21 a31	a12 a22 a32
прибыль р. 1 пр.	C1	C2

Составить план выпуска продукции, тобы при её реализации получить максимальню прибыль.

Пусть х1, х2 – кол-во единиц продкции первого и второго вида. Тогда z =C1x1 +C2x2 -> max - целевая функция Ограничение на переменные:

, x1,x2 0

3)Математическая модель задачи составления рациона

Пример. При откормке каждое животное должно получать не менее b1 питательного вещества S1,не менее b2 s2, b3 – S3. Содержание количества единиц питательных веществ в одном кг каждого из кормов k1 и k2 а также стоимость одного килограмма корма приведены таблице.

	кол-во ед. пит. в-в на 1 кг корма
	k1	k2
S1 b1 S2 b2 S3 b3	a11 a21 a31	a12 a22 a32
ст-ть 1кг корма	C1	C2

Составить дневной рацион нужной питательности, чтобы затраты на него были минимальными.

Решение. Пусть х1, х2 – кол-о кг кормов k1 и k2. Тогда общая стоимость:

z =C1x1 +C2x2 -> min

, x1,x2 0 - математическая модель задачи.

От неравенств такого вида можно перейти к уравнениям, введя доп. положительную переменную:

В общем виде: z =C1x1 +….Ckx2 -> max(min)

,

4)Свойство решений задачи лп(теорема о max(min) целевой ф-ции)

Рассм. ЗЛП экономической формы:

: z =C1x1 +C2x2+….Ckx2 -> max(min) (1)

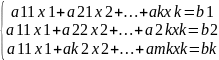(2)

Теорема. Многогранник решений соотв. опорному плану; и наоборот- каждому опорному плану в системе (2) соотв. угловая точка многогранника решений.

Билет № 5

Св-во решений задачи ЛП (опорные планы)

Рас-им ЗЛП канонич. Формы Z = С₁X₁ +C₂X₂ + ….C_nX_n max (min) (1)

a₁₁ x₁ + a ₁₂ x ₂ + …..a _1n x _n = B₁

a₂₁ x₁ + a ₂₂ x ₂ + …..a _2n x _n = B₂

_{……. ………………}

A_m1 x₁ + a _m2 x ₂ + …..a_mn x _n = B_n (2)

Люб-ое решение си-мы уравнения (2) будет называться планом или допустимым решением, а мн-во всех решений сис-мы (2) многогранником решений. План Х = (х₁, х₂, ..,хn) наз. Опорным, если векторы – столбцы в матрице (2) соответствует ненулевым координатам плана линейно – независимы. Опорный план наз. Невырожденным, если число ненулевых координат плана = m – числу уравнения в си-ме (2). План наз. Оптимальным, если на нем достигается min (max) целевой функции (1).

Каждой угловой точке многогранника решений соответствует опорный план и наоборот, каждому опорному плану си-мы ур-ний (2) соответ. Угловая точка многогранника решений.

Билет № 6

Графический метод решения ЗЛП

Расс-им ЗЛП с двумя переменными х₁ и х₂

Z = c₁x₁ + c₂x₂ max(min) предположим, что в ограничении также 2 перемен. х1 и х2. Тогда многогранник решений будет многоугольником на плоскости. При этом прямая на плоскости наз. опорной, если он а имеет с многогранником решений хотя бы 1 общую точку и он целиком располагается по одну сторону от нее.

Алгоритм графич. метода

Строим многогранник решений. Находим градиент Z. (С₁, С₂) задает направление наибольшей возрастающей целевой функции. Рассмотрим линию уровня скалярного поля Z = c₁x₁ + c₂x₂ и двигаем данную прямую в направлении перпендикулярно Z max далеко возможно пока она не станет опорной .

Пример 1

Z = x₁ + x₂ max (2, 2)

Построить многогранник решений 1

x₁ – 2x₂ ≥ -2

2x₁ – x₂ ≤ 2 градиент Z (1, 1) 2 1

x₁ ,x₂ ≥ 0 z_max = z (2, 2) = 2+2 = 4

• 2

Билет № 7

Симплекс метод решения ЗЛП ( переход от первоначального опорного плана к другому)

Рассмотрим ЗЛП z = c₁x₁ + c₂x₂ + …..c_nx_n max

x₁ + a_1m+1 + a_{1m + 2}x_m+2 + …..+ a_1nx_n = b₁

x₂ + a_2m+1 + a_{2m + 2}x_m+2 + …..+ a_2nx_n = b₂

…… …………….

x_n + a_mn+1 + a_mn+1 x_m+1 + …..+ a_nmxm_n = b_m

Так как правя часть больше 0, то базисному решению Х₀ = (В1, В2, Вm будет опорным планом. Перейдем к другому базисному решению введя в базис переменную Xn + 1 и введем X1. В ре-те получим новое базисное решение

X₁ = (0; b₂ – (b₁/a₁*m+1)a_2m+1 ; b₃ – b₁/a_{m + 1};……; b_m – (b₁/a_1m+1)*a_nm+1;b₁/a_1m+1;0)

Х1 – новое базисное решение. Для того, чтобы это решение было планом необход., чтобы все координаты были больше 0.Если в задаче(1) (2) переходить от класс Х0 к Х1, план Х1 – опорный. Найдем зн. целевой функции z на плане x1. Если все оценки плана Х0 больше 0, тоХ0 будет оптимальным. Перенесем ф.(3) в виде: z(x₁) = z(x₀) – b₁/a_1m+1

Значение z преобразовывается так же как и коэф-ты в матрице си-мы (2) при переходе от одного базиса к другому. Можно показать 0, что аналогичным образом преобр-ся оценки в планах, когд переходим от одного плана к другому. При этом оценка плана получается, если из целевой функции искл. все базисные переменные. При решении задач по симпликс методу в рассм. Матрицу добавляют дополнительную строку. При этом план будет оптимальным, если все оценки больше 0.

Билет № 8

Теорема об оптимальном плане

Теорема.

Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продук­ции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.