Дискретные марковские процессы.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Марковские процессы делятся на два класса:
– дискретные / марковские цепи;
– непрерывные марковские процессы.
Дискретным марковским процессом называется случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
ПОСТАНОВКА ЗАДАЧИ
Система S имеет n возможных состояний S1, S2, …, Sn (n может быть и бесконечным). Смена состояний происходит, будем считать, мгновенно, в строго определенные моменты времени tl, l = 1, 2 … . В дальнейшем, временные точки tl будем называть шагами. Известны вероятности Pij перехода системы за один шаг из состояния Si в состояние Sj.
Цель моделирования: определить
вероятности
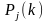перехода системы после k-го
шага, где
(не путать с вероятностями Pij).
Если переходные вероятности Pij стационарные, т.е. от времени не зависят или иначе от шага к шагу не меняются, то марковская цепь называется однородной. В противном случае, если Pij зависят от времени, то марковская цепь называется неоднородной. Значения Pij предполагаются известными и обычно сводятся в матрицу переходных вероятностей.
,
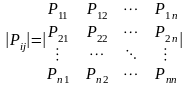причем
.
Графически это можно отразить с помощью графа:
P24
Вероятности P11,
P22, P33,
P44 можно не
указывать, т.к. данные вероятности
вычисляются из остальных. Например,
.
Математической моделью нахождения вероятностей состояния однородной марковской цепи является рекуррентное выражение:
,
где – это вероятность j-того состояния системы после k-того шага.
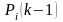– это вероятность i-того
состояния системы после (k-1)-го
шага.
Для неоднородной марковской цепи определение вероятностей состояния системы находится по формуле:
,
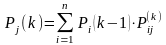– значение переходных вероятностей
для k-го шага.
Пример 1. По группе из четырех объектов производится три последовательных выстрела. Матрица переходных вероятностей имеет вид:
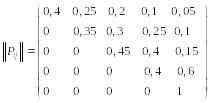
Найти вероятности состояний группы объектов после третьего выстрела.
Размеченный граф состояний приведен на рис. 2.
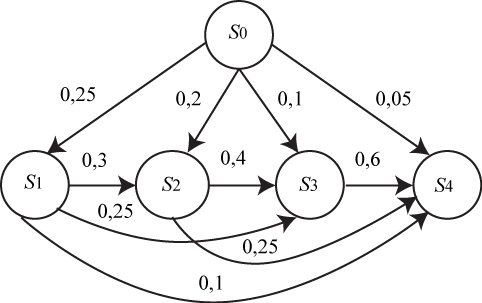
Рис. 2.
Решение.
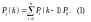
Используем выражение (1).
Так как до первого
выстрела все объекты целы, то
.
После первого выстрела все значения
вероятностей
соответствуют первой строке матрицы
переходных вероятностей. Рассчитаем
вероятности остальных состояний.
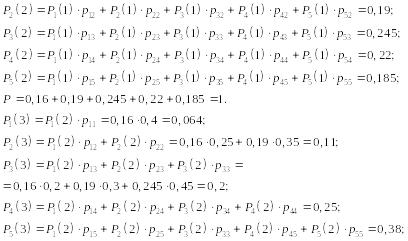
Методика моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Записать матрицу переходных состояний.
5. По рекуррентной зависимости (1) определить искомые вероятности.
Моделирование по схеме непрерывных марковских процессов.
Существует широкий класс систем, которые
меняют свои состояния в случайные
моменты времени. Как и в предыдущем
случае рассматривается процесс в системе
с дискретными состояниями S1,
S2, ... , Sn.
Оценка эффективности таких систем
определяется с помощью вероятностей
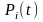каждого состояния на любой момент
времени t.
В непрерывных марковских процессах мы не можем воспользоваться переходными вероятностями Pij, т.к. вероятность перехода системы из одного состояния в другое в фиксированный момент времени равна нулю как вероятность конкретного значения непрерывной случайной величины. Поэтому вместо переходных вероятностей вводится в рассмотрение плотности вероятностей перехода:
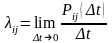(3),
где
– вероятность того, что система,
находившаяся в момент времени t
в состоянии Si
за время Δt перейдет
в состояние Sj.
С точностью до бесконечно малой второго порядка и формулы (3):
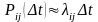(4)
Если плотность
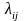не зависит от t (момента
начала промежутка
),
то процесс называется однородным, а в
противном случае – неоднородным. Целью
моделирования является определение
вероятностей состояния системы
.
Методика моделирования.
1. Определить состояния системы и
плотности вероятностей переходов
.
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части
записывается производная вероятности
-го
состояния
.
5. В правой части записывается
алгебраическая сумма произведений
и
.
Число произведений столько, сколько
стрелок связано с данным состоянием.
Если стрелка графа направлена в данное
состояние, то соответствующее произведение
имеет знак плюс, если из данного состояния
— знак минус.
6. Определить начальные условия и решить систему дифференциальных уравнений.
Пример 2. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рис. 3.
Решение
Очевидно,
.
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова
необходимо задать начальные условия.
Для рассмотренного примера 2 можно
задать такие начальные условия:
.
Однородный марковский процесс с
непрерывным временем можно трактовать
как процесс смены состояний под влиянием
некоторого потока событий. То есть
плотность вероятности перехода можно
трактовать как интенсивность потока
событий, переводящих систему из
-го
состояния в
-е.
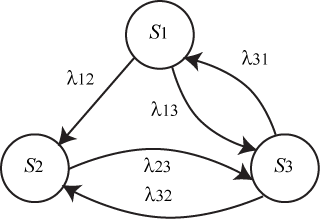
Рис. 3
При исследовании сложных объектов необходимо выяснить, возможен ли в исследуемой системе установившийся режим. Ответ на этот вопрос дает теорема Маркова, которая применительно к непрерывным марковским процессам формулируется так:
Теорема
Маркова:
Если процесс однородный, и из каждого состояния возможен переход за конечное время в любое другое состояние, и число состояний конечно, то предельные значения существуют, и их значения не зависят от выбранного начального состояния.
На схеме по рис. (б) система имеет установившееся значение.
Схема «гибели и размножения».
Граф состояний процесса «гибели и размножения» показан на рис. 5.
Особенностью модели является наличие прямой и обратной связей с каждым соседним состоянием для всех средних состояний; первое и последнее (крайние) состояния связаны только с одним «соседом» (с последующим и предыдущим состояниями соответственно).
Название модели — «гибель и размножение» — связано с представлением, что стрелки вправо означают переход к состояниям, связанным с ростом номера состояния («рождение»), а стрелки влево — с убыванием номера состояний («гибель»).
Рис. 5
Составлять уравнения Колмогорова нет необходимости, так как структура регулярна, необходимые формулы приводятся в справочниках.
Для приведенных на рис. 5 обозначений формулы имеют вид:
(2)
Пример. Имеется система из двух одинаковых и работающих параллельно СС.
Требуется определить надежностные характеристики этой системы.
Решение
В этой системе возможны три состояния:
— оба СС исправны;
— одно СС исправно, другое ремонтируется;
— оба СС неисправны и ремонтируются.
Будем полагать, что процессы отказов и восстановлений — однородные марковские, одновременный выход из строя обеих СС, как и одновременное восстановление двух отказавших СС практически невозможно.
Поскольку СС одинаковые, то с точки зрения надежности, неважно, какое именно СС неисправно в состоянии , важно, что одно. С учетом сказанного, ситуация моделируется схемой «гибели и размножения» (рис. 6).
На рис. 6:
— интенсивности
потоков отказов;
— интенсивности
потоков восстановлений.
Пусть среднее время
безотказной работы каждого СС
,
а среднее время восстановления одного
СС
Тогда интенсивность
отказов одного СС будет равна
,
а интенсивность
восстановления одного СС —
.
В состоянии работают оба СС, следовательно:
В состоянии работает одно СС, значит:
В состоянии восстанавливается одно СС, тогда:
В состоянии восстанавливаются оба СС:
Используем зависимости (2). Вероятность состояния, когда оба СС исправны:
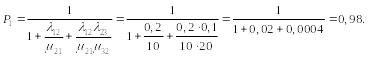
Вероятность второго состояния (работает одно СС):
Аналогично
вычисляется и
.
Хотя найти
можно и так:
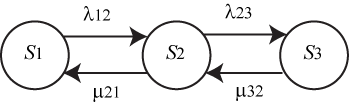
Рис. 6