Ортогональность собственных функций

Функции и называются ортогональными, если при . Здесь V – объём, где определены эти функции.

Собственные функции эрмитового оператора, принадлежащие различным собственным значениям, ортогональны друг к другу.

Пусть и – соответствующие собственные числа. Из основного свойства эрмитового оператора известно, что . Тогда и, т.к. при , то , следовательно, функции и – ортогональны.

Набор функций таких, что и называется ортонормированной системой.

Если (причём в этом ряде может быть и бесконечное число членов), то u называется полной функцией. При этом .

Представление физических величин посредством операторов

Постулаты квантовой механики:

1. Состояние движения частицы описывается волновой функцией .

2. Каждая динамическая переменная представляется определённым линейным эрмитовым оператором.

3. При измерении числового значения некоторой физической величины, изображаемой оператором с определённой вероятностью получается одно из чисел , являющихся собственными числами . Вероятность получения при измерении того или иного значения вычисляется с помощью следующего правила: Пусть – собственные функции , т.е. . Функции представляют собой ортонормированную систему. Разложим  по . Вероятность того, что при измерении физической переменной, обозначенной будет получено равна .

4. Волновая функция  подчиняется уравнению Шредингера.

Вычисление средних значений физических переменных: .

, т.к. система ортонормированная.

Оператор координаты: , где – плотность распределения координаты. Отсюда следует, что оператор координаты сводится к умножению функции на координату: (в одномерном случае).

Оператор импульса: Проекция оператора импульса на ось x , где – проекция импульса на ось x. Видно, что , т.е. оператор импульса .

Энергия, выраженная через координаты и импульс, называется функцией Гамильтона: .

Оператор энергии: .

Оператор момента импульса: .

Формулы, которые в классической механике служат для связи между численными значениями физических величин, в квантовой механике следует рассматривать как формулы, связывающие операторы этих величин.

Для того, чтобы различные динамические переменные могли одновременно иметь определённые численные значения, необходимо и достаточно, чтобы соответствующие им операторы были коммутирующими.

1. Пусть и . Тогда и .

2. Пусть и . Тогда 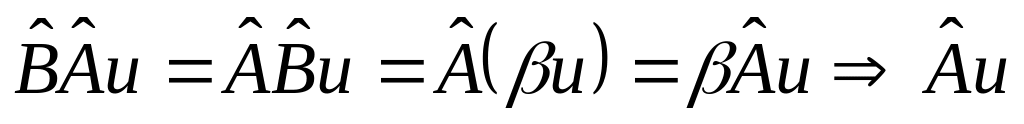– собственная функция , т.к. собственные функции отличаются на постоянный множитель.

Одномерная потенциальная яма

П усть потенциальная энергия частицы задаётся функцией и где-то находится частица. Тогда её волновая функция подчиняется уравнения Шредингера: . В областях, где частица находится не может, так как чтобы она туда попала, нужна бесконечно большая энергия. Тогда при . В других областях . Тогда это уравнение можно записать так: . Характеристическое уравнение: . Решение уравнения: . Волновая функция должна быть непрерывной, следовательно, и . Отсюда следует, что либо , либо . Но, если , то , т.е. частицы нет нигде, что противоречит условию. Следовательно, , где n – целые числа, причём , т.к. при и . Константа A определяется из условия нормировки:

Таким образом, , где .

Р ассмотрим процесс налетания частицы на потенциальный барьер. Пусть сначала энергия частицы . Уравнение Шредингера для этого случая: . Оно преобразуется в два: , где . В этой функции слагаемые с положительными степенями описывают частицу, бегущую вправо, а с отрицательными – влево, причём первое уравнение – до столкновения с потенциальным барьером, а второе – после. Частица полностью проходит сквозь барьер, следовательно, , т.к. эта часть описывает частицу, движущуюся влево после столкновения, чего быть не может, так как энергия частицы достаточно велика для прохождения сквозь барьер. Волновая функция должна быть непрерывна: . Коэффициент отражения .

Пусть теперь . Тогда уравнение Шредингера будет таким: , следовательно, . , т.к. . При этом есть вероятность того, что частица пройдёт сквозь барьер, если он конечной длины. Коэффициент прохождения , где l – область барьера.