37 Вопрос…Первообразная для данной функции. Неопределённый интеграл и его простейшие свойства

Первообра́зной данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция   является первообразной  . Так как производная константы равна нулю,   будет иметь бесконечное количество первообразных; таких как   или   … и т. д.; таким образом первообразных функции   можно обозначить как  , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Неопределённый интегра́л для функции   — это совокупность всех первообразных данной функции.

Если функция   определена и непрерывна на промежутке   и   — её первообразная, то есть   при  , то

  , где С — произвольная постоянная.

Если  , то и  , где   — произвольная функция, имеющая непрерывную производную

Свойства   неопределенного   интеграла 

В приведенных ниже формулах f  и  g - функции переменной x, F - первообразная функции f,  а, k, C - постоянные величины.









38.Вычисление неопределенных интегралов способом подстановки

Алгоритм вычисления неопределенного интеграла методом подстановки :

1Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).

2Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.

3Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.

4 Производят замену под интегралом .

5 Находят полученный интеграл .

6В результате производят обратную замену, т.е. переходят к старой переменной. Результат полезно проверять дифференцированием.

Найти интегралы :

1) ) )

Введем подстановку :

Дифференцируя это равенство, имеем:

Выразив отсюда , получим: . Подставив в данный интеграл вместо и их выражения, получим:

)⁴ .

39 Вычисление неопределённых интегралов с помощью интегрирования по частям.

40 Разложение рациональных дробей на простейшие

Продолжение далее….

41. Интегрирование рациональных дробей, знаменатели которых имею только вещественные корни.

43. Понятие определённого интеграла. Свойства определённого интеграла.

44. Теорема о среднем для определённого интеграла.

46. Формула Ньютона-Лейбница.

47. Вычисление определённого интеграла с помощью замены переменной.

48 Вычисление определённого интеграла с помощью интегрирования по частям.

49. Вычисление площадей плоских фигур в прямоугольных координатах.

Пусть функция f(х) непрерывна на сегменте [а;b]. Если f(х )≥0 на [а; b] то площадь S криволинейной трапеции, ограниченной линиями у =f(х), у = 0, х = а, х = b, равна интегралу

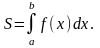
Если же f(x) ≤ 0 на [а; b] то — f(х) ≥ 0 на [а; b]. Поэтому площадь S соответствующей криволинейной трапеции выразится формулой

или

Е сли, наконец, кривая y=f(х) пересекает ось Ох, то сегмент [а;b] надо разбить на части, в пределах которых f(х) не меняет знака, и к каждой такой части применить ту из формул, которая ей соот­ветствует.

П

Рис 9

ример. Найти площадь плоской фигуры, ограниченной параболой y = x², прямыми х=1, х = 3 и осью Ох (рис 9) . [1]

Решение. Пользуясь формулой , нахо­дим искомую площадь

S =

П

Рис 10

ример. Найти площадь плоской фигуры, ограниченной графиком функции у = sinх и осью абс­цисс при условии (рис 10). [1]

Решение. Разбиваем сег­мент [0; ] на два сегмента [0; ] и [ ; 2 ]. На первом из них sinx ≥ 0, на втором — sinx ≤ 0. Следовательно, ис­пользуя формулы

и , имеем, что искомая площадь