1. Приложения определённого интеграла бывают: физические, экономические, геометрические.

Геометрические: площади плоских фигур, длины дуг плоских и пространственных кривых, объёмы тел по площади поверхности сечения, объёмы тел вращения, площади поверхности вращения.

Площади поверхности плоских фигур:

y=f2(x) f1(x)≤y≤ f2(x); a≤x≤b y=f1(x)

x =φ(t) y=ψ(t), tϵ[α;β]

Площадь криволинейного сектора
Вычисление длины дуги кривой.	(параметрически) (декартовая система координат)
пространственная кривая, и х = j(t), у = y(t) и z = Z(t)	(декарт.) ,  = f() (полярн.)
Объем тела вращения. тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b]
заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x).
Площадь поверхности вращения.

2. Несобственный интеграл 1-ого рода – интервал на бесконечном промежутке от ограниченной функции. Это число I, равное:

1. . Он называется сходящимся, если существует конечный предел частичного интервала . В противном случае он расходящийся.   

2. . Он называется сходящимся, если существует конечный предел частичного интервала . В противном случае он расходящийся.

3. . Разбивается на два интеграла: . Сходится, если сходятся оба интеграла. В противном случае – расходится.

Несобственный интеграл 2-ого рода – интеграл по конечному промежутку от неограниченной функции.

Несобственный интеграл 2-ого рода с особенностью на правой границе называется сходящимся, если существует конечный предел частичных сумм. Сходным образом дают определение н.и.2-ого р. на нижнем пределе интегрирования внутри промежутка.

3. Пусть D-некоторое множество точек на плоскости Оху. Величина Z называется функцией переменных величин x и y на множестве D, если каждой точке этого множества соответствует одно определенное значение величины Z и пишут.

Число Z называется значением функции f в точке (х; у). Переменную Z называют зависимой переменной, а переменные x и y – независимыми переменными (или аргументами); множество D – областью определения функции.  Упорядоченная пара значений x и y называется точкой М(х;у), а функция двух переменных - функцией этой точки Z=f(M). Областью определения функции в этом случае является некоторое множество {M} точек плоскости.

ОПРЕДЕЛЕНИЕ: Число А называется пределом функции Z=f(M) в точке M₀, если функция Z=f(M) определена в окрестности точки M₀ и для любого ε>0, δ>0 такое что при |M₀M|<δ, выполняется неравенство |f(M)-A|<ε.

ОПРЕДЕЛЕНИЕ: Функция Z=f(M) называется непрерывной в точке M₀, если предел функции в этой точке существует и равен значению функции в этой точке, т.е.

Поскольку точки   непрерывности функции   задаются условием  , то часть свойств функций, непрерывных в точке  , следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.

ТЕОРЕМА: всякая элементарная ф. м. п. непрерывна в каждой точке области определения.

4. Z = f(x,y) определена в окрестности (х₀;у₀). Частные функции по переменной Х обозначаются: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной. Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. 

Геометрическое изображение функции двух переменных.

Рассмотрим функцию z = f(x,y) , определенную в некоторой области М на плоскости Оху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где , является графиком функции двух переменных. Поскольку уравнение определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.

z

z = f(x,y)

M y

Примеры:

z = ax + by + c

и поверхностей второго порядка:

z = x² + y² (параболоид вращения),

(конус) и т.д.

Для функций, заданных явно z = f(x;y):

Уравнение касательной плоскости:

Прямая, проходящая через точку Мо и перпендикулярная касательной плоскости, построенной в этой точке, называется нормалью.

Уравнение нормали:

Для функций, заданных неявно F(x,y,z) = 0:

Уравнение касательной плоскости:

Уравнение нормали:

5. Определение 2.1. Полным приращением функции u = f(x, y, z) называется

Теорема 2.1. Если частные производные существуют в точке (х₀ , у₀ , z₀) и в некоторой ее окрестности и непрерывны в точке (x₀ , y₀ , z₀) , то

,

где α, β, γ – бесконечно малые, зависящие от Δх, Δу, Δz.

Можно показать, что где . Действительно, α, β и γ – бесконечно малые при ρ→0, а - ограниченные (т.к. их модули не превышают 1).

Тогда приращение функции, удовлетворяющей условиям теоремы 2.1, можно представить в виде: ,

где

Определение 2.2. Если приращение функции u = f (x, y, z) в точке (x₀ , y₀ , z₀) можно представить в виде (2.3), (2.4), то функция называется дифференцируемой в этой точке, а выражение - главной линейной частью приращения или полным дифференциалом рассматриваемой функции.

Обозначения: du, df (x₀ , y₀ , z₀).

Так же, как в случае функции одной переменной, дифференциалами независимых переменных считаются их произвольные приращения, поэтому

Необходимое условие дифференцируемости функции в точке: если функция дифференцируется в точке, то она в ней непрерывна.

6. Если функция имеет непрерывные частные производные в некоторой точке, то она в ней дифференцируема. При этом:

dz(x₀,y₀)= y, при этом dx=x-x₀, dy=y-y₀

7. Если z=f(x,y) диф-ма в точке , функции x=φ(t), y=ψ(t) диф-мы в т. t_о , то функция сложной функции вычисляется по формуле:

Следствие: если в дополнение к условиям x=φ(u,v), y=ψ(u,v), то:

8. z=f(x,y) - числовая (или скалярная) функция, то говорят, что она задаёт скалярное поле.

Линией уровня ф-ии 2-ух переменных наз-ся линия, в каждой точке которой одно и то же постоянное значение: z=C  f(x,y) = C

Функция, где больше 3-ёх перемен.: поверхность, на которой функция принимает одно и то же значение, наз-ся поверхностью уровня: u=f(x,y,z), u=C  f(x,y,z)=C

Производная скалярного поля в Мо в направлении единичного вектора l=(cosα,cosβ,cosγ) наз-ся число: . Она равно проекции градиента по направлению: : /

Вектор, координатами которого в каждой точке некоторой области являются частные производные функции u = f (x, y, z) в этой точке, называется градиентом функции u = f (x, y, z).

Обозначение: grad u = .

Свойства градиента.

1. Производная 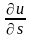по направлению некоторого вектора S равняется проекции вектора grad u на вектор S.

2. Производная в данной точке по направлению вектора S имеет наибольшее значение, равное |grad u |, если это направление совпадает с направлением градиента.

3. Производная по направлению вектора, перпендикулярного к вектору grad u , равна нулю.

4. Если z = f (x,y) – функция двух переменных, то grad f = направлен перпендикулярно к линии уровня f (x,y) = c, проходящей через данную точку.

9. Частные производные высших порядков.

z=f(x,y)
z`x		z`y
z``xx	z``xy	z``yx	z``yy

Теорема о смешанной производной: если функция имеет непрерывную производную до n-ого порядка включительно в т. Мо, то в этой точке

10. Частные производные функции z = f (x,y) являются, в свою очередь, функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:

Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д.

Частной производной n-го порядка функции нескольких переменных называется первая производная от производной (n – 1)-го порядка.

Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например, ).

Дифференциалом второго порядка функции u = f (x, y, z) называется

Кратко:

Дифференциалом порядка k называется полный дифференциал от дифференциала порядка (k – 1): d ^k u = d (d ^k-1 u).

Свойства дифференциалов высших порядков.

1. k-й дифференциал является однородным целым многочленом степени k относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные k-го порядка, умноженные на целочисленные постоянные (такие же, как при обычном возведении в степень): .

2. Дифференциалы порядка выше первого не инвариантны относительно выбора переменных.

11. Функция у от х, определяемая уравнением F (x, y) = 0, называется неявной функцией.

Условия существования однозначной и непрерывной неявной функции:

Пусть:

1. существует т. ( : F( _0,у₀)=0

2. В окрестности этой точки функция непрерывна и диф-ма, причём .

Тогда

а) в некоторой окрестности точки (х₀ , у₀ ) уравнение определяет у как однозначную функцию от х: y = f(x);

б) при х = х₀ эта функция принимает значение у₀: f (x₀) = y₀ ;

в) функция f (x) непрерывна.

Дифференцируемость.

Пусть функция у от х задается неявно, где функция F (x,y). Пусть, кроме того, - непрерывные функции в некоторой области D, содержащей точку (х,у), причем в этой точке . Тогда функция у от х имеет производную

Пример. Найдем , если . Найдем , .

получаем: .

12. S: F(x,y,z)=0, Mo(x_o,y_o,z_o) ϵ S

Полагаем, что F имеет непрер. частн. производ. в окрестности т. Мо, причём F`z(Mo) . Тогда уравнение касательной: F`x(Mo)(x-x_o)+F`y(y-y<sub>o</sub>)+F`z(z-z_o)=0

уравнение нормали:

13. локальный экстремум функции многих переменных. Необходимое условие экстремума.

Определение 1. Пусть функция f(x₁, ..., x_m) определена на множестве  . Внутренняя точка   называется точкой локального максимума (минимума), если существует такая окрестность U(M₀) точки М₀, что для всех М(х₁, ..., х_m)   U(M₀) выполняется неравенство f(M)   f(M₀) [f(M)   f(M₀)].

Определение 2. Точка М₀ локального максимума или локального минимума называется точкой локального экстремума.

Теорема (Необходимое условие локального экстремума). Пусть функция f(x₁, ..., x_m) определена в некоторой окрестности т.  , дифференцируема в точке М₀, и имеет в этой точке локальный экстремум, тогда все частные производные первого порядка функции f в т. М₀ равны нулю: