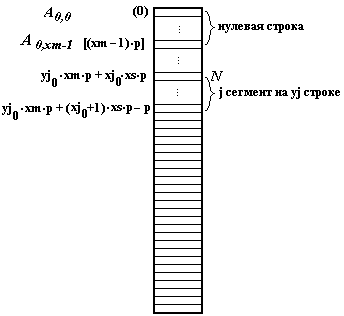3. Специфика оценок в математике распознавания.

Функции распределения вероятности в системах распознавания могут быть заданы аналитически или таблично. В практике анализа принято использовать функционалы от них, которые в практических задачах получают реальный смысл и их использование входит в стратегию выводов.

Наиболее употребимы определения точек ожидания появления событий, это математическое ожидание, медиана, мода. Для одномерного пространства исходов это скаляры, для многомерного - вектора.

Математическое ожидание можно определить по плотности функции распределения - , или по выборке размером - , где - порядковый номер зафиксированного события , изменяется от 0 до , недостоверные отсчеты не фиксируются. Данная характеристика получила еще название абсциссы центра тяжести плотности распределения случайной величины. Не достоверные выбросы, которые в ряде случаев сильно смещают этот параметр. Преобразование выбросов происходит при превышении измерением интервала . Обычно, они заменяются на граничные значения со стороны выброса. Не смотря на все процедуры существенно зависит от выбросов и используется не часто.

Медиана ( ) определяет координаты точки, относительно которой появление событий справа и слева равновероятно. Другое определение – абсцисса прямой, параллельной оси ординат и делящей фигуру под плотностью вероятности на две одинаковой площади. Для возрастающего ряда без интерполяции можно записать:

, где , - границы интервала проявления , знак выделяет условие, которому должен удовлетворить переменная, в данном случае выбираются только те, для которых . Ориентация на медиану оправдана тогда, когда величина отклонения случайной величины от интервала положения медианы не играет роли и важно только попадание в цель. При этом процедура распознавания применяется многократно. Медиана более устойчивая к аномальным явлениям характеристика, чем математическое ожидание.

Мода ( ) выделяет точку или отрезок на оси, на котором величина плотности вероятности имеет максимальное значение. Другое определение – абсцисса наиболее вероятного события. .

Мода часто выбирается в качестве цели при однократном применении решения. Эта характеристика наиболее чувствительна к помехам и не четкости информации, чем математическое ожидание.

Перечисленные параметры оценивают координату ожидаемого результата. Возможна в практическое применение и их комбинации, как нелинейная так и линейная, например, величина : , где , , - коэффициенты доверия и .

Вторым по важности параметром является оценка ожидания разброса случайной величины. Эти оценка могут быть выражена числом, или интервалом на оси абсцисс, а для многомерных величин эллипсоидом, нередко носящим имя эллипсоида рассеяния.

На практике для симметричных по плотности вероятности законов наибольшее применение получили функционалы вида: или , где - номер зафиксированного события (0-n), - номер канала, , - абсцисса канала, вероятность попадания события в канал, на графике плотности вероятности (0-g), - показатель степени, положительная величина, целая или дробная, определяет метрику данного критерия.

При =1, говорят об оценке разброса через величину среднего арифметического отклонения, при =2, оценивается разброс через величину среднеквадратичного или стандартного отклонения. Чем выше величина , тем более влияют выбросы в измерениях и соответственно величина отклонения.

Определим усредненную симметричную оценку параметра разброса случайной величины при наличии неопределенности в задании коэффициента . , где коэффициенты доверия оценки отклонения с - показателем степени и ; - порядковый номер функционала со степенным коэффициентом , изменяется от 1 до - числа конкурирующих оценок.

Оценка интервала (его границ), существования проявлений объектов исследуемого события, обычно ведется при задании ограничения на вероятность появления события вне интервала или внутри интервала.

Рис.3.1. Интервалы анализа

Для одномерного случая с равным распределением вероятности ошибки определения интервала справа и слева границы доверительного интервала можно определить, как

, , где - заданная вероятность ошибки, min_x, max_x границы интервала учета событий.

Определение доверительного интервала позволяет уменьшить пространство исходов. Множество центральных моментов точек класса образуют зону этого класса, среди них обычно определяется точка наиболее приближенная к распознаваемой. Ее либо называют наихудшими, если отнесение объекта к классу является ошибкой, или наилучшей, если результат распознавания верен.

Изменение вида плотности вероятности в распознавании не так очевидно. Вернемся к рис. 1.1. Очевидно зоны I, III содержат объекты, распознаваемые по факту наличия сигнала в зонах. Значение напряжения в этих зонах не учитывается. Введя два новых класса подлежащих распознаванию (возможно дуб и возможно ольха) увидим кривые распределения вероятности их характеризующие. Эти кривые являются пронормированными остатками «крыльев» плотностей распределений прежних классов, попавших в зону II.

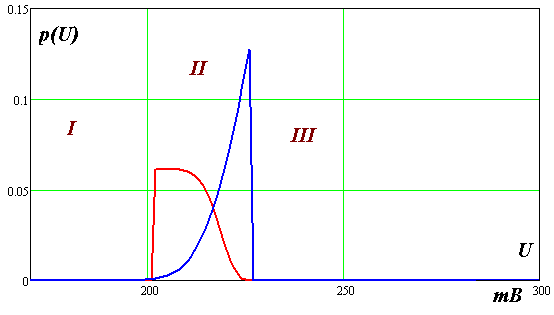
Рис.3.1а. Плотности вероятности величин сигнала при поступлении на конвейер

досок «возможно дуб» (более темная структура) и «возможно ольха»

Очень часто одно из граничных значений координаты появления события берется за исходную точку для осторожного принятия решения, которое обычно ориентируется на наихудшее стечение обстоятельств. Эта координата соответствует появлению наиболее не желательного события. В этом случае вводится понятие допустимой вероятности появления более неблагоприятного события, чем те которые учитываются. Исходя из этого ограничения, определяется наиболее важная граница доверительного интервала.

Наряду с естественными системами координат, описывающими пространство исходов, используются и искусственные системы. Например, из координат трехмерного пространства и времени формируются системы пространственных и временных частот.

В таких системах так же задаются интервалы существования объектов одного класса.

Свойства объектов, участвующих в распознавании, получили название признаков, а их набор – алфавита признаков.

Изображения после ввода их в память компьютеров, ЦПС, микроконтроллеров имеют вид слитного массива с пиксельным описанием. Интуитивно и, как показывает практика, более корректно при программировании его представить двумерным массивом, состоящим из строк и столбцов.

Сегментация неизбежный атрибут обработки изображений, широко применяемый при распознавании образов. Разбиение изображения на фрагменты позволяет ограничить размер исходных файлов. В выделенных сегментах, содержащих исследуемые объекты, проводится их дальнейшая обработка. Это позволяет сократить объем пространства исходов и понизить вычислительную нагрузку на систему обработки данных.

Простейшее формирование сегментов для последующей обработки заключается в выделении прямоугольного окна, перемещающегося по массиву.

Пусть координата столбца – x отсчитывается слева направо, координата строки – y сверху вниз. Сформируем бегущий сегмент и зафиксируем его на характерных участках объектов.

Рис.3.2. Сегмент в поле изображения	Рис.3.3. Сегмент в памяти

Пусть исходное изображение имеет размеры ym, xm. Назначим размеры сегмента ys, xs и зададим шаг сегмента по столбцу и строке – hy, hx. Размер строки анализа xm равен целому числу шагов hx плюс размер сегмента xs. Число строк анализа ym равно целому числу шагов hy плюс размер сегмента ys.

Общее количество сегментов в строке nx, в столбце ny и по полю ns будут равны:

, где floor – целая часть числа.

Введем текущий номер сегмента j от нуля и определим координаты первого пикселя сегмента yj, xj:

, , где mod(x,a) – остаток от x по модулю a.

Сегмент с текущим номером j (например: r(j)) сформируем как субматрицу из общей матрицы (R), указав начало и конец субматрицы по столбцу и строке: .

Реальный адрес ячеек в памяти для последнего пикселя в строке, если адрес первого пикселя ,

, где - размер описания пикселя в байтах.

Адрес первого пикселя ( ) сегмента в памяти устройства распознавания на шаге .

Адрес первого пикселя следующей строки данного сегмента .

Рассмотрим методику формирования описаний объектов на примере задачи сортировки интегральных схем различных типов. На Рис.3.4 представлено изображение корпусов различных микросхем. Ниже в таблице представлены выбранные сегменты корпусов, фона и гистограммы цветовых составляющих их описаний.

Рис.3.4. Корпуса интегральных микросхем

В таблице 3.2 и на рисунках 3.5-3.7 проведены величины интегральных параметров и их взаимное положение в пространстве исходов.

Абсолютные значения сигналов редко на практике используются в качестве координат пространства исходов. Они зависят от множества факторов – освещенности и т.п. Поэтому рассмотрим более стабильные параметры, для чего разделим цветовые компоненты сигналов на суммарный сигнал на объекте и определим доверительные интервалы существования объектов в пространстве исходов.

Таблица 3.1.

Металл	Фон	Пластик	Керамика
1	2	3	4

Таблица 3.2.

Металл	Фон	Пластик	Керамика
1		3	4
185 184 162	153 201 233	18.27 81.05 52.84	194 171 158
15.26 12.14 12.03	8.33 3.51 8.16	10.88 10.77 14.14	31.31 38.31 31.29
0.082 0.066 0.074	0.054 0.017 0.035	0.595 0.133 0.267	0.162 0.224 0.198

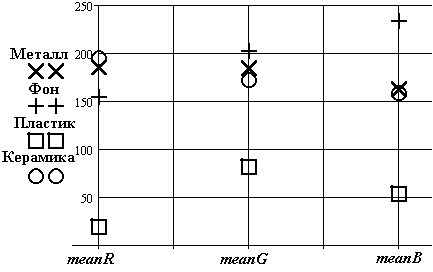
Рис.3.5. Оценка величин математического ожидания

Рис.3.6. Оценка величин среднеквадратического отклонения

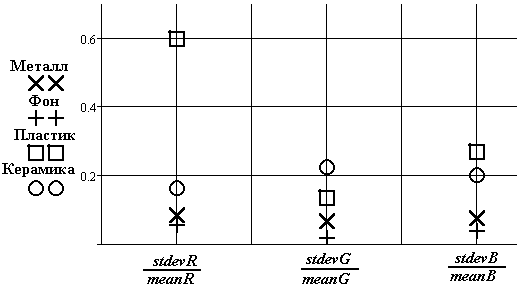
Рис.3.7. Оценка относительных величин среднеквадратического отклонения

; ; где - 1-4 порядковый номер объекта.

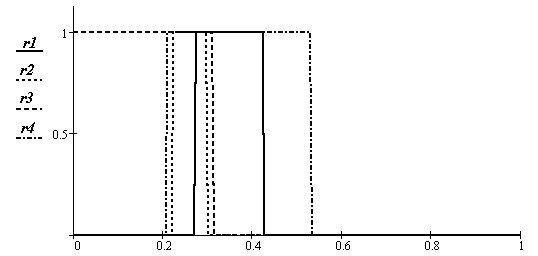
Рис.3.8. Оценка доверительных интервалов нормированного красного

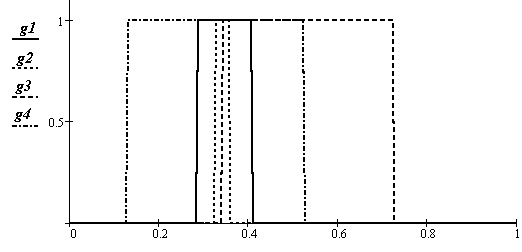
Рис.3.9. Оценка доверительных интервалов нормированного зеленого

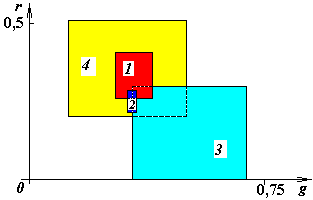
Рис.3.10. Оценка доверительных интервалов с предположением равномерной вероятности появления признака у объекта по всему доверительному интервалу

На рис. 3.8 и рис. 3.9 приведены графики доверительных зон по и компонентам раздельно. Интегральные зоны показаны на рис. 3.10 и рис. 3.11. На первом из них не учитывается понижение вероятности появления обеих признаков на краю зон, в этом случае описание зон существования объектов имеет вид прямоугольников. Более правильное их представление – упрощенными эллипсоидами рассеяния показано на втором рисунке. Номера параметров соответствуют номерам объектов в таблицах 3.2, 3.3.

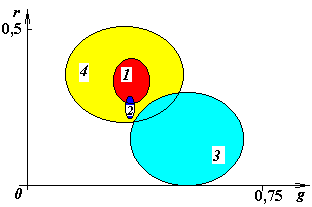
Рис.3.11. Оценка доверительных интервалов при понижающейся к границе интервала вероятности появления признака у объекта

Приведенный пример пробного, прикидочного исследования признаков объектов не свободен от ряда упрощений и неточностей.

Рассмотрим их в ходе рекомендуемой методики проведения исследований положения объектов, классов в пространствах признаков и ситуаций.

1. Определитесь с целью исследования – формализуйте задачу. Это важный этап, он может привести к, так называемым, системным ошибкам в постановке и решении задачи. Исправить последствия этих ошибок чрезвычайно сложно, практически решение задачи придется начинать заново. В рассматриваемом примере мы ставим задачу распознавания четырех объектов по RGB описаниям их пикселей с телекамеры низкого качества.

2. Наберите достаточный статистический материал об объектах рассматриваемых классов. Мы ограничились выборкой 600 слитных точек с объектов. Практически взято по одному зашумленному сегменту без фильтрации (результат хорошо виден на примере объекта №4 - керамический корпус в сегменте соседствует с металлической пластиной). Такой выбор возможен только при поверхностном анализе. В практике распознавания объектов по их изображениям число точек включаемых в анализ превышает сотни тысяч, а главное их необходимо брать с различных объектов исследуемого класса, в различных условиях наблюдения и освещения. Практическая рекомендация – информация с одного экземпляра объекта только одно измерение, пусть при этом проанализировано несколько тысяч пикселей. Корреляция между параметрами точек на объекте достаточно велика и это делает отсчеты зависимыми.

3. Постройте гистограммы и по их виду сделайте оценку формы функций распределения, рассчитайте рабочие функционалы, планируемые в алфавит признаков. Стремитесь использовать мало зависящие от внешних условий параметры. Мы выбрали признаки 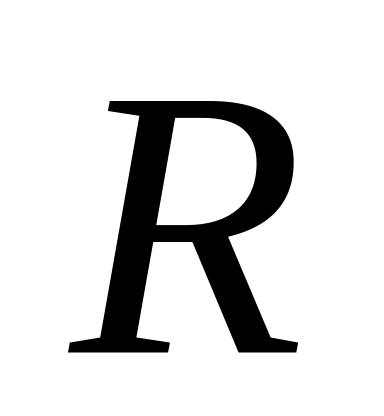, , 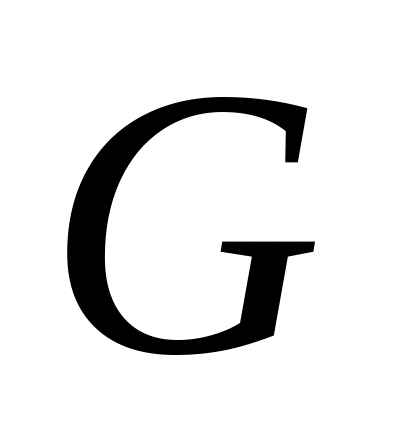описания и их среднеквадратичные отклонения, вычислили и относительные величины.

Постройте доверительные интервалы существования объектов классов в пространстве признаков. Современные компьютеры, математические пакеты позволяют проводить довольно большие объемы исследований в короткие сроки. Наиболее просто для визуального анализа отобразить положение классов в пространстве двух признаков.

Если области существования классов пересекаются, увеличьте количество признаков или измените существующие. На рис. 3.10 объекты классов практически не различимы по выбранным признакам.

На рис. 3.12 представлены области существования классов по измененным признакам. В качестве последних выбраны выражения 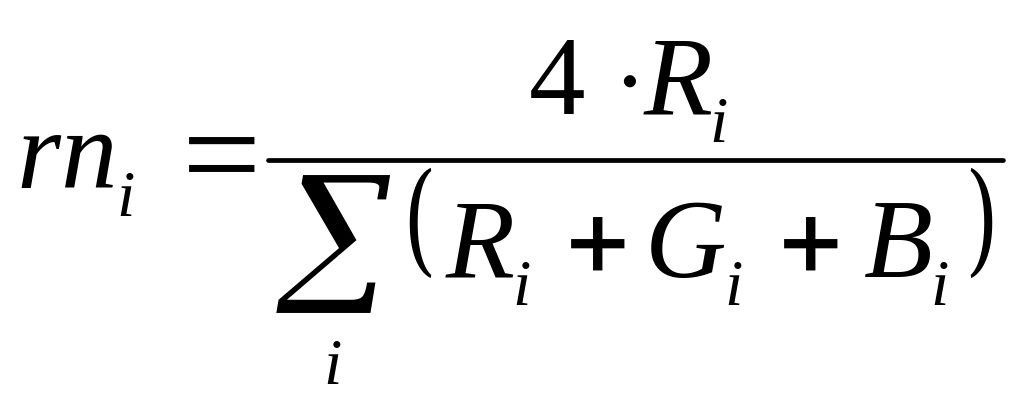, , что практически означает нормировку по интегральному световому потоку со всех объектов.

На рис. 3.12 представлен результат – класс пластиковых корпусов (№3) в данном пространстве резко выделен и различим.

Необходимо учитывать то, что формализованные алгоритмы стандартных расчетов даже на объемных массивах данных в тысячи пикселей выполняются в миллисекунды, поэтому рабочий алфавит признаков может содержать несколько десятков компонентов. Все полученные значения ожидаемых оценок случайных величин – каждый столбик гистограммы, оценки центральных моментов сами по себе случайные величины. Для корректного использования они должны удовлетворять определенным требованиям, вернее стремиться соответствовать им:

• При увеличении числа испытаний они должны стремиться к истинной величине параметра, с ростом объема данных разница между искомым значением и расчетным - 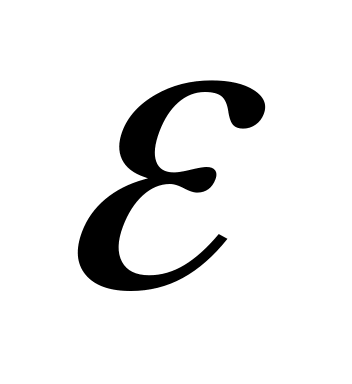должна становиться сколь угодно малым числом ( при 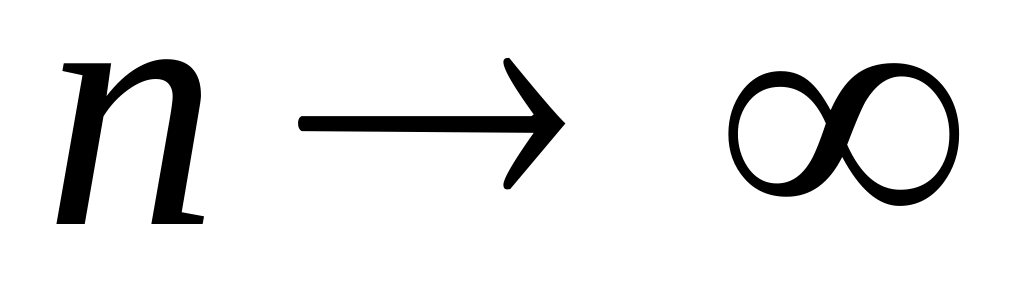). Такие оценки получили название состоятельных.

• Оценка считается несмещенной, если она не содержит систематических составляющих погрешности Оценка должна быть эффективной, т. е. обеспечивать минимальный разброс в оценке искомой величины в заданном объеме исследований.

Первое требование не всегда можно обеспечить, так как эргодических случайных описаний образов на практике не так много. Окружающий нас мир непрерывно развивается и практически все свойства объектов имеют определенную тенденцию изменения значений (тренд). Поэтому наибольший вес в анализе имеют “свежие” данные.

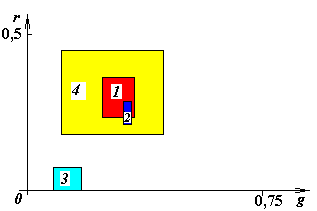
Рис.3.12. Оценка доверительных интервалов с предположением равномерной вероятности появления признака у объекта по всему доверительному интервалу и нормировкой по общему световому фону

Важной спецификой в анализе исходных данных является и очень большой объем возможной информации, можно потратить жизнь, изучая специфику изображений определенного класса, например, бровей на лице человека, выбирая все большее количество объектов. Это с одной стороны.

С другой стороны достаточно в течении нескольких часов проанализировать несколько десятков реализаций, что бы вложить стартовый материал в систему распознавания лиц форму бровных дуг в рабочий алфавит.

В развивающейся интеллектуальной системе компоненты алфавита признаков непрерывно корректируются, при этом вес последней информации, как правило, выше веса данных более ранних.

Аппаратное вычисление параметров закона распределения, плотности распределения одна из традиционных основных составных частей математической статистики. Специфика ТР конкретизирует решение данной задачи. При анализе статистического ряда рекомендуется следующая последовательность действий:

• определение математического ожидания ;

• определение среднеквадратичного отклонения ;

• прореживание статистического ряда;

• задание метрики оси абсцисс и числа каналов;

• подсчет чисел событий попавших в каналы;

• при близости полученной гистограммы к известным законам

распределений заменяют исследуемую гистограмму известной кривой распределения.

Отметим специфику некоторых из перечисленных операций.

При прореживании статистического ряда корректируются недостоверные отсчеты с номером , таких что , на практике не редко их не удаляют, а перемещают в ближайшую точку доверительного интервала, это позволяет сохранить метрику сетки последовательных отсчетов, что важно при проведении корреляционных, спектральных исследований.

Количество каналов анализа задается исходя из соображений по - требуемой компактности описания конкретного класса, реального объема выборки, потерь от недостоверного определения формы функции плотности вероятности.

Вычислительная нагрузка возрастает в квадратичной степени и более резко от увеличения объема описания классов. Конкретный вид зависимости определяется сложностью алгоритмов распознавания.

Число событий попавших в канал является в каждом эксперименте случайной величиной и величина ее доверительного интервала зависит от числа событий принимающих участие в эксперименте, а положение его еще и от параметров, вида функции плотности распределения вероятности исследуемого события.

При малом числе испытаний определение доверительного интервала наиболее корректно через биноминальный закон распределения - закон Бернулли.

На рис. 3.13, 3.14, 3.15 приведены графики плотностей распределения этого закона для различных чисел опытов. События не зависимы.

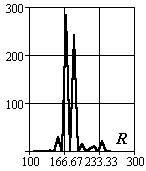
Рис.3.13. Вид плотности распределения вероятности появления событий в канале

при числе опытов 6 (подстроченные индексы функций 5 и 1)

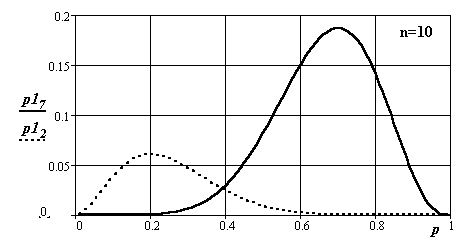
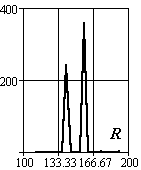
Рис.3.14. Вид плотности распределения вероятности появления событий в канале

при числе опытов 10 (подстроченные индексы функций 7 и 2)

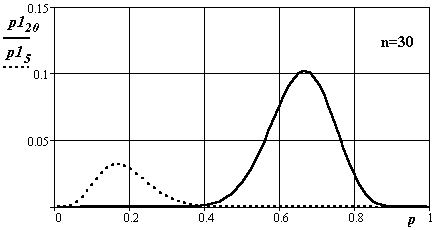
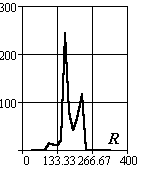
Рис.3.15. Вид плотности распределения вероятности появления событий в канале

при числе опытов 30 (подстроченные индексы функций 5 и20)

Исследуемый процесс подчинен равномерному закону распределения и может принимать значения от 0 до n. Индексы при p1. Величина отношения значения индекса к n – искомая вероятность.

Во всех случаях математические ожидания, полученные в экспериментах, совпадают с искомыми. С ростом числа экспериментов дисперсии определения оценок плотности вероятности уменьшаются. Изменяется и вид кривых распределения – они становятся симметричней и приближаются по форме к нормальному распределению.

Реально при n > 10 целесообразнее в силу его простаты и распространенности пользоваться графиками нормального закона.

Центральная предельная теорема (ЦПТ) в теории оценок говорит о том, что при большом числе случайных явлений их средние характеристики перестают зависеть от каждого отдельного явления и получают устойчивость т. е. перестают быть случайными. Пользуясь ими можно распознавать случайные явления и предсказывать поведение случайных процессов. Для сумм случайных отсчетов, фигурирующих в оценках функций распределения и их параметров можно записать: , где - номера отсчетов, , - нормировочный, и весовой коэффициенты учета отсчета в итоговой сумме. .

Математическое ожидание и дисперсия случайной величины для независимых по ЦПТ равны:

, .

Для и - , , , а среднее квадратичное отклонение оценки величины уменьшается с ростом .

Усреднение лежит в основе подавляющего числа исследований в вообще и определения зон существования классов в пространстве признаков.

На первый взгляд различные по величине отсчеты не так уж часты. Но в практике систем распознавания при самообучении новая информация и та, что отражает накопленный опыт соседствуют рядом. Новая информация имеет большую достоверность, чем предыдущие отсчеты того же объема. Тем не менее оценка на основании накопленного опыта, в следствии, интеграции большего объема данных, характеризуется высокой достоверностью. При этом дисперсии могут отличаться на порядок. Однако накопленный опыт не содержит детальной предыстории. Один из простейших выходов из ситуации, но довольно рациональный, это эволюционная корректировка данных, например, с .

Изложенный подход используется при определении всех параметров законов распределения и его вида.

При определении дисперсии уменьшают делитель на единицу, отображая тот факт, что число независимых данных при расчете дисперсии меньше на единицу общего количества отсчетов.

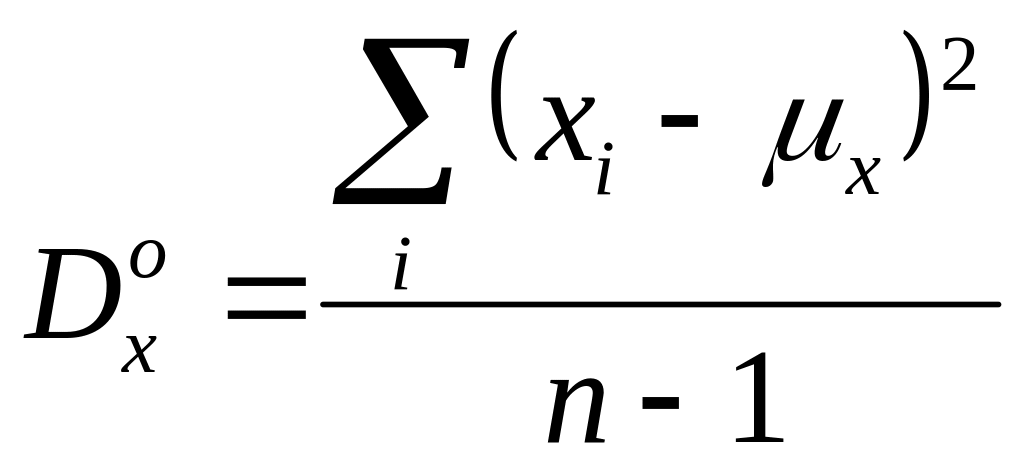. Эта оценка не смещенная. Дисперсия оценки величины дисперсии

, где - четвертый центральный момент, зависящий от вида закона распределения, для нормального закона распределения и , для равномерного распределения и .

Интервальные оценки формируют не точки, а области существования случайных признаков. Если вид закона распределения не известен, то используют методику определения величины доверительного интервала через параметры закона распределения Стьюдента. В этом случае абстрагируются от параметров закона распределения. Ориентируются на число опытов и заданную вероятность появления события. Величина доверительного интервала тогда , где - коэффициент Стьюдента. Данный коэффициент находится из одноименного закона распределения исходя из заданной величины вероятности попадания в доверительный интервал. Вид плотности распределения для числа степеней свободы : 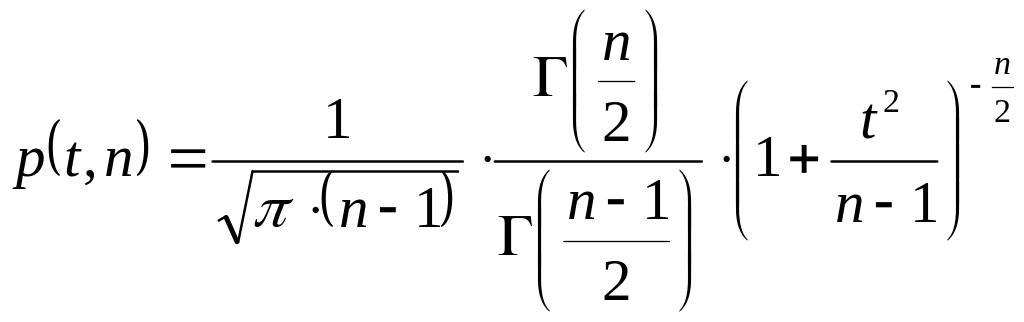, де - гамма функция. Интегральное распределение задает величину доверительного интервала.

На рис. 3.16, 3.17 показано влияние заданной величины вероятности промаха от числа опытов и значения коэффициента.

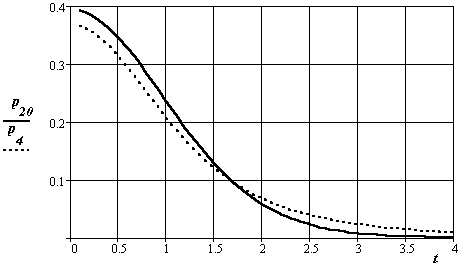
Рис.3.16. Вид плотности распределения вероятности Стьюдента в зависимости

от величины коэффициента (индексы - числа опытов 20 и 4)

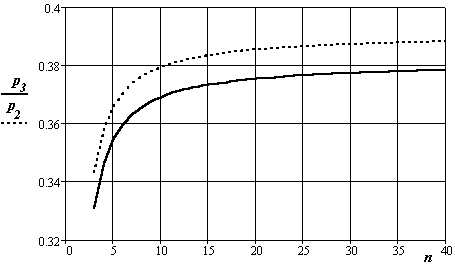
Рис.3.17. Изменение участка распределения вероятности Стьюдента в зависимости

от величины коэффициента (индексы - числа опытов 3 и 2)

Графики повторно показывают практическое снижение влияния числа опытов на вид закона распределения величины оценки доверительного интервала при числе независимых отсчетов более 10.

Гистограмма оценивает вероятность появления события в определенной зоне пространства признаков.

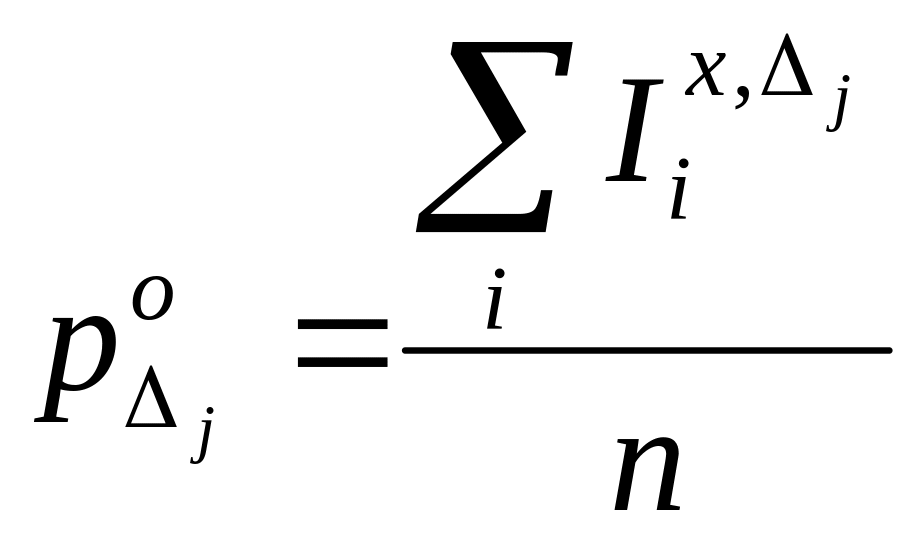, где - индекс появления события на участке . В отсчете , он равен 1 при появлении события на участке и 0 если был промах. Данная оценка не смещенная. Ее дисперсия .

Интервальные оценки позволяют, с определенной оговоркой, судить о эффективности проведенного статистического анализа положения объекта x на оси признака. Это важно для самообучающихся систем распознавания. Например, часто используют расстояние от до наихудшей в распознавании точкой класса от отнесенное к доверительному интервалу оценки математического ожидания ( ): . Это показатель достоверности статистических исследований и применяется обычно, как коэффициент доверия к проведенным исследованиям.

Приведенные выражения работают только при независимости отсчетов, отстоящих друг от друга на расстоянии большим, чем радиус корреляции.

Большие возможности применения корреляционных представлений в физических и технических науках открылись с возникновением корреляционного анализа случайных функций, которое можно отнести к 1920г., когда Тэйлор ввел понятие корреляционной функции. Важное значение имело установление в 30-х годах прошлого столетия Н. Винером и А. Я. Хинчиным связи между корреляционными и спектральными характеристиками случайных процессов.

Реально встречающиеся случайные функции очень часто можно считать нормальными, а каждая нормальная случайная функция может быть полностью описана в рамках корреляционной теории. Однако, изображения содержат перекрывающиеся объекты, т. е. на лицо нелинейное преобразование и эти объекты слабо связаны друг с другом. В то же время и для случайных функций, не являющихся нормальными, эта теория дает ответ на целый ряд важных вопросов. Выделим два направления по использованию аппарата корреляционного анализа:

• применение корреляционных функций и их параметров в качестве характеристик распознавания сигналов,

• применение корреляционных функций в качестве характеристик идентифицирующих системы передачи информации.

К первому из указанных направлений можно отнести исследования, относящиеся к распространению волн, в том числе радиоволн, звуковых волн. Сюда входят и исследование шумов различной физической природы, статистических свойств изображений; анализ отдельных звуков речи и слогов; применение в геофизике и метеорологии; применение в биологических и медицинских исследованиях и т. д.

Во второй группе ведущее место занимает экспериментальное определение корреляционных характеристик объектов; оно позволяет выяснить динамические свойства объектов по данным их нормальной работы без применения каких-либо искусственных возмущений и играет весьма важную роль при проектировании систем. К этой же группе относятся корреляционные методы снижения влияния искажений, вносимых при передаче сигнала, оценки качества переходных процессов в линейных системах; исследования акустических характеристик помещений, измерения звукоизоляции и звукопоглощения; определения частото-контрастных характеристик систем наблюдения.

Уже приведенный здесь беглый перечень дает представление о значении и достаточно широком распространении корреляционного анализа.

В курсе наибольшее внимание уделяется распознаванию объектов по форме и параметрам взаимно корреляционных функций между исследуемым объектом и эталонами классов.

Величина корреляционной функции может быть представлена следующим образом:

,

или расширив пространство исходов временными осями процессов ( , ) получим

.

Положив , получим автокорреляционную функцию процесса . Таким образом, автокорреляционную функцию можно рассматривать как частный вид взаимной корреляционной функции.

Автокорреляционные и корреляционные функции зависят как от степени взаимосвязанности случайных процессов, так и от дисперсии этих процессов. Для того чтобы получить меру взаимосвязанности, абстрагированную от величин дисперсии, производят нормирование корреляционных функций. Нормированные корреляционные функции называют коэффициентами корреляции:

.

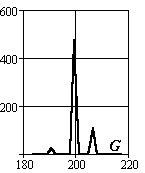
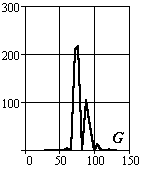
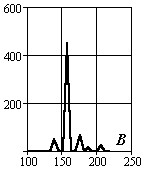
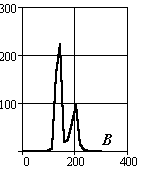
В практике широко используется представление описаний классов в производных пространствах. Наиболее широко рассматриваются поиск отличительных признаков объектов в области пространственных частот. На рис. 3.18 представлены модуль частотного спектра изображения рамки и на рис. 3.19 его сечение. Видны четко участки преобладающих частот, которые можно использовать как признаки. Отчетливо виден выброс амплитуд частот на участке отводов чипа. Характерным для изображений является и наличие пика на частотном портрете на нулевых частотах, практически это общий фон яркости. Он чаще всего не информативен, удалить влияние его на вид графиков, можно либо вычитанием среднего фона по цветовым составляющим, либо смещением по изображающим осям.

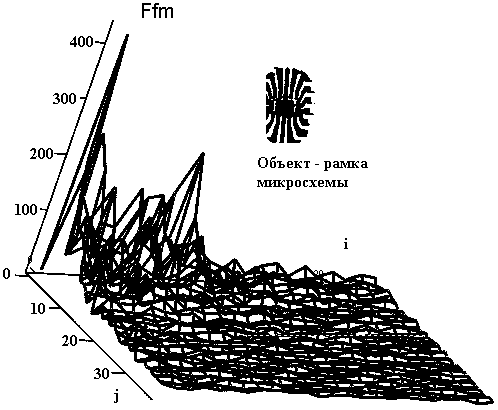
Рис. 3.18. Фурье образ R составляющей сегмента рамки

С учетом корреляционных соотношений и понятий верхних и нижних частот (временных для случайных процессов, пространственных для объектов в 3 мерном пространстве) уточним понятия оценки дисперсии параметров случайной величины.

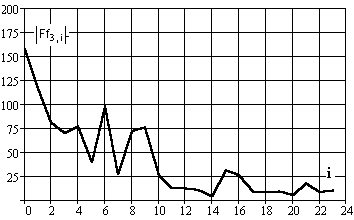
Рис.3.19. Сечение Фурье образа R составляющей сегмента рамки

Для оценки математического ожидания, получаемой накоплением данных за временной интервал

.

И здесь связь с корреляционной функцией. Довольно часто принимают ,

где , , параметры характеризующие размах, скорость спада частоту колебаний корреляционной функции. Во всяком анализе, важно определить минимально необходимое число экспериментов, позволяющее провести исследования с требуемой точностью.

Для вычисления с погрешностью менее 5% от необходимо интегрировать данные не менее . Например: при =0,2 , 102 с.

Реально данные поступают дискретно с интервалом (во времени, в геометрическом пространстве и т. п.) , где =1, 2, ... и =1, 2, ... слагаемые номера отсчета.

Для 2% точности вычисления корреляционной функции необходимо , часто выбирают , или , где - максимальная частота важная для анализа и учета.

Два раздела математической статистики тесно связаны с процедурой распознавания:

• проверка статистических гипотез, в ходе которой выбирается вид закона распределения наиболее подходящий для описания исследуемого события;

• проверка статистических гипотез, в ходе которой определяются параметры закона распределения.

В обеих случаях устанавливается степень согласия принятых решений с реальным объектом. Выводы и последовательность действий, полученные в ходе решения этих задач вошли в методическую базу теории распознавания.

Сходство исследуемого закона распределения в числовом эквиваленте определяется критериями согласия. Первый из них (введен Пирсоном) вычисляется по плотностям вероятности и базируется на взвешенных суммах квадратов отклонений значений реальной гистограммы от «математического ожидания» гистограмм процессов рассматриваемого класса (например, нормального). , где - весовой коэффициент увеличивающий значение малых вероятностей рассматриваемого класса, l – число каналов гистограммы, принятых в расчете, , – число опытов и число в канале. Проанализируем бегло этот критерий. Это полином. Видим симметричную, квадратичную функцию штрафов за промах. В реальных задачах применительно к распознаванию вид коэффициента, вид функции требуют уточнения. Не рекомендуется из-за малой достоверности использовать каналы с < 5…10.

Критерий Колмогорова работает с интегральным законом распределения и определяет меру качества согласия, как максимальное значение модуля отклонения значений законов распределения: . Конечно, здесь требуется достаточно точное знание параметров законов (классов).

Статической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость появляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статическую зависимость называют корреляционной.

Зависимость между двумя и более случайными событиями из множеств , можно представить в общем виде ,

где - множество параметров .

Рассмотрим простейший случай. Пусть реальные отсчеты в - том эксперименте порождают наборы результатов и ( ), между которыми предполагается наличие связи .

Будем искать такие , которые минимизируют функционалы отклонений (ошибок) предсказания величины по значениям .

В качестве рабочего функционала ошибки примем сумму квадратов отклонений

.

Будем искать решение в точках экстремума, дифференцируем выражение по компонентам вектора .

, где =1... .

Это нелинейных уравнений и в общем случае они аналитически не решаются.

Для поиска линейной зависимости между двумя величинами решение существует.

,

,

,

,

.

Решая систему уравнений, находим

,

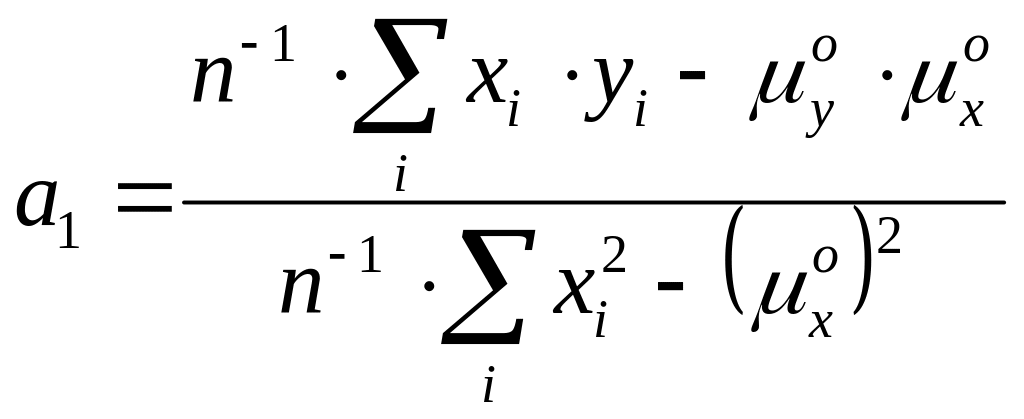, где - оценки математических ожиданий.

Задавая исходный участок по не большим по размеру и расширяя его с проверкой постоянства параметров (через их положение в доверительном интервале оценок) можно получить кусочно-линейную оценку функциональной зависимости для большинства случаев анализа компонентов пространства признаков. При нарушении постоянства (при выходе за пределы доверительного интервала) вводится новый участок. Реально аналитические выражения существуют и для квадратичного вида зависимости.

Близок по методологии к описанному, только с ориентацией на границу участка, и метод опорных векторов в ТР. Описание классов по множеству обучающей выборки также может быть сформировано по двухкоординатному пространству исходов. Рассчитываем «линию регрессии», определяем линии «доверительных интервалов» и по ним формируем оболочку класса.

Проверка статистических гипотез предполагает оценку вероятности и достоверности принадлежности закона распределения рассматриваемой случайной величины одному из известных. При этом такие понятия, как доверительный интервал оценки плотности распределения вероятности по полученной гистограмме работает и в этом случае.

Совокупность известных и включенных в описание гистограмм составляют набор классов.

Проведенные исследования добавляют в рассмотрение новую гистограмму, которая может быть отнесена к известному классу.

Такой подход стандартен в составление описания классов, т. е. часть описания класса может быть заменена ссылкой - именным индексом на известные описания свойств одного из классов.

Для примера воспользуемся генератором случайных чисел и сгенерируем вектор из 1000 чисел. Найдем разницу в оценке гистограммы реализации (рис. 3.20) и теоретического распределения (рис. 3.21).

Рис. 3.20. Нормированная гистограмма вектора из 1000 чисел, распределенных по нормальному закону	Рис. 3.21. Плотность распределения с параметрами исследуемого вектора

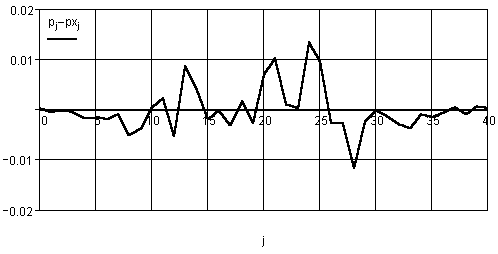
Рис. 3.22. Погрешность отнесения гистограммы реального вектора к теоретическому закону

График разности приведен на рис. 3.22. Вычислим интегральную оценку ошибки по формуле

. Расчетная величина 0,03.

Из приведенного примера можно сделать вывод о том, что реальная погрешность представления гистограммы случайного вектора чисел теоретической гистограммой или одной из известных всегда будет иметь место.

Методика определения подходит или нет один из имеющихся в базе данных классов гистограмм для исследуемого класса может быть представлена последовательностью следующих шагов:

1. Вычисляем нормированную гистограмму исследуемого вектора данных (нормировка заключается в делении чисел в каналах на общее число учтенных реализаций).

2. Генерируем известные графики распределений.

3. Определяем разность между гистограммой исследуемого вектора и известными.

4. Определяем метрику риска или потери полезности и вычисляем интегральный параметр ошибки.

5. По наименьшему (где - индекс класса) данного параметра выбираем искомый класс.

6. Проверяем на допустимость ошибки, если ошибка не допустима формируем описание исследуемого класса с новой формой функции распределения, внося ее в базу данных распределений.

Если ошибка допустима, проверяем гипотезу статистической достоверности принадлежности реализации случайной величины к известным по форме и параметрам законам распределения.

Для проверки формы функции обычно используют критерии согласия Пирсона или Колмогорова. Проверка гипотез о значении параметра функции распределения заслуживает в нашей теме более детального рассмотрения.

Для простоты, задачу о параметре функции распределения - мерной случайной величины ( ) рассмотрим, как проверку двух гипотез и . При этом и .

Эту задача является классической и об ошибках 1-го и 2-го родов рассуждают с давних времен. Как не покажется странным, это часто встречающаяся ситуация в радиолокации (цель, помеха), в промышленности (годен, брак). Не редко говорят об стремлении человека, сводить ситуации к решению финишной бинарной задачи и т.п. В таких ситуациях различают ошибки первого и второго рода. Эти понятия сильно связаны с целью исследований и они возникают при ожидании определенного объекта. Например, цели в локации, брака изделия в технологии, болезни в медицинском исследовании и т. п. Ошибка 1-го рода возникает при пропуске искомого объекта, например, пропуск цели в локации, пропуск больного человека. Последствия ошибки 1-го рода предполагают значительно большие расходы и качественно менее желательны. Ошибка 2-го рода – ложная цель принимается за искомую. В локации – ложная тревога.

На рис. 3.23 показаны плотности распределения вероятностей сигналов от двух конкурирующих объектов.

Ось признака позволяет разбить график на три зоны. Зоны I и III – детерминированы, в них однозначно определены решения по распознаванию объектов. Вторая зона предполагает наличие решающего правила, которое связано с целью решения и потерями от ошибочных решений. Например, минимизировать ошибку средних потерь. Пространство решений полное т. е. .

В работе Дуда Р., Харта П. ось х - показания фотодиода, который установлен над конвейером с движущимися досками двух типов – дуб и ясень .

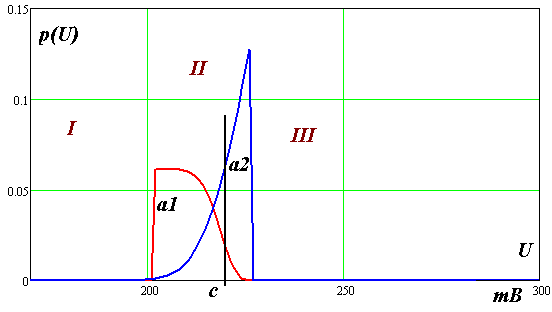
Рис.3.23. Плотности вероятности величин сигнала при поступлении на конвейер

досок «возможно дуб» (более темная структура) - a1 и «возможно ольха» - a2 и порог принятия решения c

Решение данной задачи ищется через отношение правдоподобия. Отношение правдоподобия или коэффициент правдоподобия определяется по формуле

,

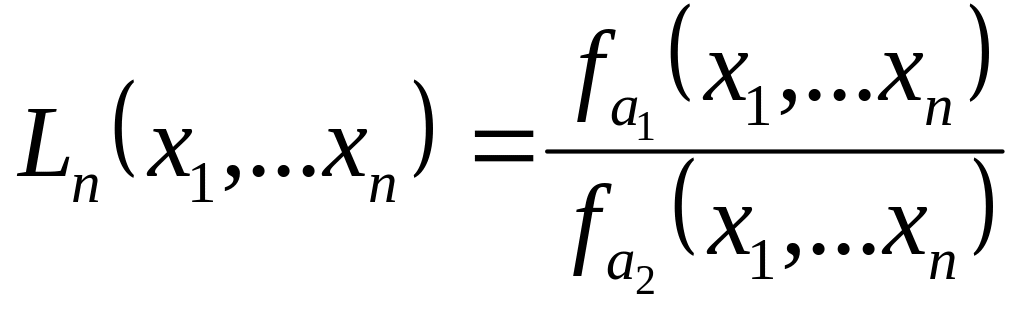где вероятность того, что при конкретной реализации имеет место событие .

Вывод о событии делается если , где - порог принятия решения .

Реально величина порога зависит от многих факторов и прежде всего от допустимой вероятности принятия не правильного решения.

Ошибка первого рода - принимается решение , а это , обозначим вероятность такого решения .

Ошибка второго рода - принимается решение , а это , обозначим вероятность такого решения .

Часто данные ошибки имеют символьное описание, например, в локации пропуск цели, ложная тревога или в промышленности риск изготовителя (отбраковано хорошее изделие), риск потребителя (получен брак). Очевидно продолжение испытаний (рост ) приводит при слабо коррелированных к понижению и .

Т. е. порог принятия решения в общем случае является функцией платы за ошибочные решения, допустимой вероятности ошибки первого или второго рода и числа испытаний , , . Задание такого порога при ограничении на или позволяет минимизировать . При заданном минимизировать или .

Для однородной независимой выборки, введя логарифмирование, получим логарифм коэффициента правдоподобия , который также широко используется на практике, получив название "различимости" , в точке .

.

В теории распознавания образов часто используют понятие случайной смеси. При этом параметрическое пространство представляется конечным числом точек ,... с известной вероятность появления объекта j - . Для вектора можно вычислить конечную смесь

.

В этой трактовке классы определяются как индексы тех параметрических векторов, которые имеют не нулевые смеси.