15. Уравнения в форме Громеки-Лэмба. Преобразуем уравнения

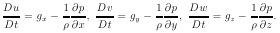
Распишем проекции полных ускорении . Отметим, что полное ускорение частицы жидко­сти — сумма местного ускорения (предела отношения приращения скорости в точке к проме­жутку времени) и ускорении вдоль линии тока. Линии тока — линии, касательные к которым указывают направление вектора скорости в точке касания в данный момент времени; опреде­ляются системой дифференциальных, уравнений dx/u = dy/v = dz/w. При стационарном (не зависящем от времени) течении линии тока совпадают с траекториями частиц жидкости, т. к. касательные к траекториям действительно дают направления движения частиц жидкости во все моменты времени.

Наложим определенное ограничение — пусть массовые (объемные силы) имеют потенциал; тогда существуют такая функция — потенциал объемных сил Р, что

Введя Р и уравнения, получим:

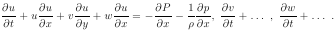
Предположим далее, что ρ = f(р) (а не ρ = ρ (p ,Т)). Такая среда называется баротропной средой (и само течение - баротропным). Для баротропных сред dp/ρ =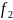 (p). Тогда dp/ρ = dП, где П = ∫dp/ρ. Конкретный вид П(р) получается, когда задана зависимость ρ = f(p). Так, для ρ=const (течении несжимаемой жидкости) получается П = р/ρ, а когда ρ=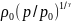 (изоэнтропное течение совершенного газа), то П = — с точностью до произвольной постоянной С.

Из тождества dp/ρ = dП следует, что

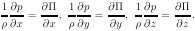
Подставим эти соотношения, кроме того, перепишем их левые части, прибавим! к ним и отняв от них одни и те же количества. На примере первого уравнении, прибавляя и вычитая получим

Выражения в скобках - удвоенные компоненты вектора, являющегося результатом приме­нения оператора ротора (вихря) к векторному полю скорости

Учитывая это, а также замечая, что

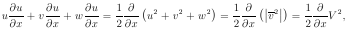
можем записать в виде векторного уравнения

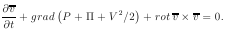
Это уравнение и есть уравнение Эйлера в форме Громеки-Лэмба.

16.Интегралы Коши-Лагранжа и Бернулли.

Уравнения Бернулли и Лагранжа-Коши. Потенциал скорости

в общем случае может быть функцией вида φ = φ(x, y, z, t), в стационарных течениях--φ =φ (x, y, z). Заметим, что ввиду независимости операций дифференцирования— dφ/dt и gradφ, можно менять их порядок:

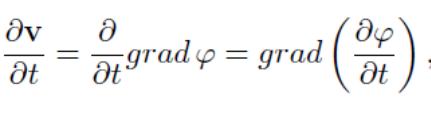
и, с учетом сказанного, в данном случае, уравнение (5.7) приводится

к виду

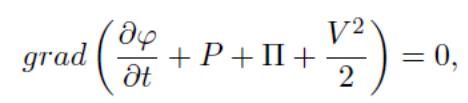
интегрирование которого приводит к выражению 1-го интеграла

уравнений движения

называемого интегралом Лагранжа-Коши. Здесь f(t) — одинаковая для всей области зависимость от времени, содержащаяся в условиях однозначности. Интеграл Лагранжа-Коши играет в теории нестационарного движения идеальной жидкости ту же роль, что интеграл

Бернулли для стационарных движений. В последнем случае dφ//dt ≡0, f(t) = const и равенство (5.8) переходит в интеграл Бернулли

в котором константа в правой части — общая для всех точек движущейся жидкости, а не, например, своя для каждой линии тока. Оба

интеграла (5.8) и (5.9) служат для выражения давления p через кинематические параметры φ, V и координаты, от которых зависит П:

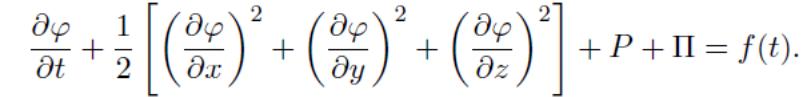
а в стационарном случае—

причем, для определения поля скоростей используем уравнение Лапласа для потенциала скорости φ:

с соответствующими ГУ. При P = gz имеем интеграл (уравнение) Бер-

нулли для несжимаемой жидкости плоском поле массовой силы

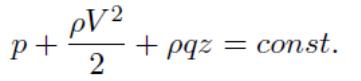
Из (5.10) видно, что в частном случае g ≡ 0 при V = 0 давление p

максимально:

Это давление p* носит название давление стационарного торможения. Так, при обтекании тела однородным потоком с параметра-

ми на «бесконечности» p∞, V∞, в «критической» точке на обращен-

ной к потоку поверхности тела для некоторой струйки тока V → 0, т. е.

происходит полное торможение потока несжимаемой жидкости и может

быть измерено давление полного торможения:

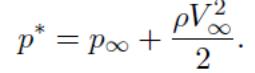
На этом может быть основано измерение скорости потока (трубкой

Пито; англ. Pitot tube, рис. НЕТ).

Рассматривая истечение из емкости через сужающееся сопло как течение идеальной жидкости получают модель «идеального сопла». Давление в емкости при V0 = 0 есть p0,что соответствует заторможенному

давлению вдоль данной струйки тока, а поскольку параметры в емкости

на удалении от сопла принимаются однородными, то полное давление

во всех струйках тока в сопле одинаково и равно p∗0 = p0. Тогда, зная

скорость потока несжимаемой жидкости в некоторой точке сопла, определим давление в ней из того же уравнения Бернулли:

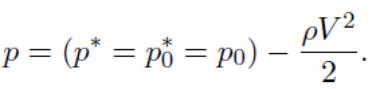
На этом основана методика измерения расхода; расходомером является сужающееся сопло, при течении маловязкой жидкости с достаточной скоростью влияние вязкости сосредоточено лишь вблизи стенок сопла; нетрудно связать скорость на срезе сопла и расход жид-

кости в нем с перепадом статических давлений между емкостью и срезом: _p = p0 −pc. Получаем формулу Эйлера для скорости на срезе Vc =√2Δp/p, для массового расхода — GТеор= pVcFc. Действительный расход G оказывается по ряду причин меньше теоретическо-

го Gтеор(по модели «идеального сопла»); при необходимости это учитывают, вводя коэффициент расхода μ = G/Gтеор≤ 1.

При течении идеальной сжимаемой жидкости справедливы те

же соображения; например, для среды с уравнением состояния совершенного газа, как указано выше, справедливо П = (λ/λ-1)(p/p), и вдоль

линий тока справедливо уравнение изоэнтропной адиабаты (Пуассо-

на): p = p0(p /p 0). Рассматривая однородный неограниченный поток

(в задачах обтекания) или истечение из емкости (в задачах истечения),

также придем к формулам, связывающим скорость потока V c термодинамическими параметрами в точке: