
2. Проверим, является ли функция четной или нечетной.
Найдем

т.к. f(-х) f(х) и f(-х) -f(х), то функция не является ни четной, ни нечетной (см. 4.4).
Значит, график функции не имеет ни оси симметрии, ни центра симметрии.
3. Найдем асимптоты.
а) Функция имеет точку разрыва II-го рода х = 0.
Т.к.

то прямая х = 0 служит вертикальной асимптотой графика функции
(см. 4.6.2).
б) Наклонную асимптоту ищем в виде у = kх + b (см. 4.6.3).
Найдем правую наклонную асимптоту при x → +∞
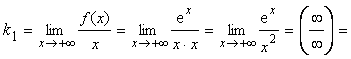
= (По правилу Лопиталя) =

= (По правилу Лопиталя) =
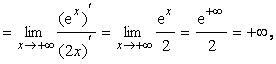
т.о., правой наклонной асимптоты нет.
Найдем левую наклонную асимптоту при x → -∞



Подставив найденные значения k2 и b2 в уравнение у = kх + b, получим у = 0.
Т.о., левая наклонная асимптота у = 0 является горизонтальной асимптотой при x → -∞.
4. Найдем интервалы монотонности и точки экстремума функции.
Найдем первую производную функции

Найдем критические точки I-го рода (см. 4.7). Приравняем первую производную у/(х) к нулю

точка x1 = 1 – критическая точка I-го рода.
Производная у/(х) не существует, когда знаменатель дроби обращается в нуль
х2 = 0 x2 = 0.
Точка x2 = 0 не может быть критической точкой, т.к. эта точка не принадлежит области определения функции (см. 4.7). Точка x2 = 0 является точкой разрыва II-го рода функции.
Составим таблицу промежутков монотонности функции (определим знак производной у/(х) в любой точке каждого промежутка).
х |
(-∞; 0) |
0 |
(0; 1) |
1 |
(1; +∞ ) |
y/ |
– |
∞ |
– |
0 |
+ |
у |
|
|
|
е |
|
|
|
точка разрыва |
|
точка min |
|
Из
таблицы видно, что функция
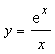 возрастает
на интервале (1; +∞)
и
убывает на интервалах (-∞; 0)
и (0; 1)
(см.
4.5).
возрастает
на интервале (1; +∞)
и
убывает на интервалах (-∞; 0)
и (0; 1)
(см.
4.5).
При переходе через точку x1 = 1 производная у/(х) меняет знак с «минуса» на «плюс», следовательно, х = 1 – точка минимума (см. 4.8)

Т.о., точка М(1; е) – точка минимума.
5. Найдем интервалы выпуклости (вогнутости) графика функции и точки перегиба.
Находим производную второго порядка



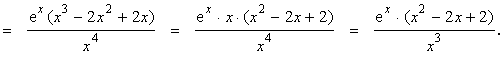
Точек, «подозрительных» на перегиб нет (см. 4.9.2), т.к. ex 0 и
х2 – 2x + 2 0 (дискриминант D = 4 – 8 = -4 < 0), а точка х = 0 не принадлежит области определения функции.
Составим таблицу промежутков выпуклости и вогнутости графика функции (определим знак второй производной в любой точке каждого интервала).
х |
(-∞; 0) |
0 |
(0; +∞) |
у// |
– |
0 |
+ |
у |
|
|
|
|
|
точка разрыва |
|
Из таблицы видно, что кривая выпукла на интервале (-∞; 0) и вогнута на интервале (0; +∞) (см. 4.9.1).
6. Используя результаты исследования, построим график функции
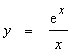 .
.
Напомним:
вертикальная асимптота х = 0;
левая горизонтальная асимптота у = 0 (при x → -∞);
наклонной асимптоты нет;
точка локального минимума M(1; e);
точки перегиба нет.
Сначала строим асимптоты и точку M, затем график функции.

Задача № 2
Требуется
найти наибольшее и наименьшее значения
функции
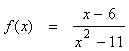 на
отрезке [-3; 2].
на
отрезке [-3; 2].
Решение (см. 4.11)
1) Функция определена везде, кроме тех точек х, при которых
х2 – 11 = 0,
т.е. при
![]() .
На отрезке [-3; 2]
функция f(x)
определена и непрерывна.
.
На отрезке [-3; 2]
функция f(x)
определена и непрерывна.
Определим критические точки I-го рода, для чего найдем производную


(см. 4.11.1).
Производная у/(х) равна нулю, когда числитель дроби равен нулю
–x2 + 12x – 11 = 0.
Корни квадратного уравнения –x2 + 12x – 11 = 0 x1 = 1 x2 = 11. Точка x2 = 11 [-3; 2].
Производная у/(х) не существует, когда знаменатель дроби равен нулю
![]()
Точки
![]() и
и
![]() не
принадлежат области определения функции.
не
принадлежат области определения функции.
Точка х = 1 – критическая точка, принадлежащая отрезку [-3; 2]
(см. 4.7).
2) Вычислим значения функции f(x) в критической точке и на концах отрезка [-3; 2] (см. 4.11)
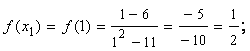
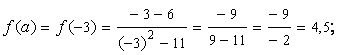

3) Функция
 достигает
при х = -3
своего наибольшего значения, т.е.
достигает
при х = -3
своего наибольшего значения, т.е.
![]() и
при х = 1
своего наименьшего значения, т.е. =
и
при х = 1
своего наименьшего значения, т.е. =
 .
.
Ответ:
![]()
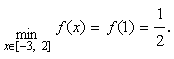
задача № 3
Требуется записать уравнения касательной и нормали
а) к кривой у = х3 – 2х + 1 в точке М0 с абсциссой х0 = 0;
б)
к кривой
![]() в
точке М1(1, 0).
в
точке М1(1, 0).
а) Решение
Функция у = х3 – 2х + 1 определена при всех х. Найдем значение у0 = у(х0) = у(0) = 03 – 20 + 1 = 1. Точка М0(0; 1) – точка касания.
Найдем производную у/(х) = (х3 – 2х + 1)/ = 3х2 – 2. Вычислим значение производной в точке х0 = 0
у/(0) = 302 – 2 = –2,
т.е. у/(х0) = – 2.
уравнение касательной к кривой (см. 4.12.1)
у – у0 = у/(х0)(х – х0).
Подставляем полученные значения х0, у0, у/(х0) в уравнение
касательной у – 1 = – 2(х – 0) или 2х + у – 1 = 0 – искомое уравнение касательной.
Уравнение нормали к кривой (см. 4.12.2)

Подставляем полученные значения х0, у0, у/(х0) в уравнение
нормали
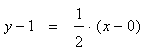 или
х – 2у + 2 = 0
– искомое уравнение нормали.
или
х – 2у + 2 = 0
– искомое уравнение нормали.
Ответ: 1) 2х + у – 1 = 0 – уравнение касательной к кривой у = х3 – 2х + 1 в точке М0(0; 1);
2) х – 2у + 2 = 0 – уравнение нормали к кривой у = х3 – 2х + 1 в точке М0(0; 1).
б) Решение
Функция
![]() определена
для х 0
точка М1(1, 0)
точка касания.
определена
для х 0
точка М1(1, 0)
точка касания.
Найдем производную у/(х) функции, заданной неявно,
![]()

![]()
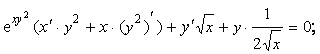
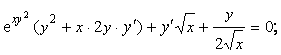
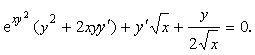
Из последнего равенства найдем значение производной у/(М1), положив х = l, y = 0

у/(М1) = 0.
Уравнение касательной к кривой F(х, у) = 0 в точке М1(1, 0)
(см. 4.12.3)
y – у1 = у/(х1, у1)(х – х1).
Подставляя полученные значения х1, у1, у/(х1, у1) в уравнение касательной, получим y – 0 = 0(х – 1) или у = 0 – искомое уравнение касательной.
Уравнение нормали к кривой F(х, у) = 0 в точке М1(1, 0)
(см. 4.12.4)
у/(х1, у1)(у – у1) + х – х1 = 0.
Подставляя полученные значения х1, у1, у/(х1, у1) в уравнение нормали, получим (у – у1)0 + х – 1 = 0 или х – 1 = 0 – искомое уравнение нормали.
Ответ:
1) у = 0
–
уравнение касательной к кривой
![]() в
в
точке М1(1, 0);
2) х = 1 – уравнение нормали к этой кривой в точке М1(1, 0).
Задача № 4
Бак с крышкой имеет форму кругового цилиндра. Площадь полной поверхности бака равна S. Каково должно быть отношение диаметра основания бака к высоте, чтобы его объем был наибольшим?
Решение
Из условия задачи составим функцию.

Пусть радиус основания бака равен R, а высота Н. Тогда площадь полной поверхности бака
S = Sосн. + Sбoк. = 2R2 + 2RH =>
S = 2R2 + 2RH.
Выразим высоту Н

Следовательно, объем бака выражается через радиус R так:
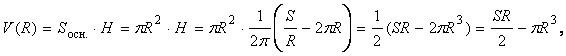
где R (0; ∞).
Задача свелась к нахождению наибольшего значения функции V(R) на интервале (0; ∞) (см. 4.11.2).
Найдем производную

Найдем критические точки I-го рода, для этого приравняем производную к нулю
![]()
![]()

![]()
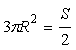

![]()

Т.к.
 не
принадлежит области определения функции
не
принадлежит области определения функции
V(R),
то –
единственная критическая точка на
интервале
–
единственная критическая точка на
интервале
(0; ∞) (см. 4.7).
При переходе через точку производная V/(R) меняет знак с «плюса» на «минус». Т.о., точка – точка максимума
функции V(R) (см. 4.8).
Т.к. на интервале (0; ∞) одна критическая точка и она является
точкой максимума (см. 4.11.2), то в ней функция достигает своего наибольшего значения.
Следовательно, объем бака будет наибольшим при .
Найдем значение функции в критической точке (в точке max)

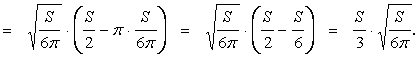
Чтобы найти отношение диаметра D = 2R1 основания бака к его
высоте
Н,
найдем высоту Н
при радиусе
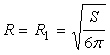



Найдем отношение диаметра бака к его высоте

Значит, отношение диаметра основания бака к его высоте равно 1.
Ответ:

