11. Свойства неопределенного интеграла.

Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.

.  Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:   2.   Hеопpедeлeнный интеграл от диффepeнциaла некоторой функции равен сумме этой функции и произвольной постоянной:

∫dF(x)= F(x)+C.

Действительно,

3.   Постоянный множитель можно выносить за знак интеграла:

  α ≠ 0 - постоянная.

4.   Неопределенный интеграл от aлгeбpaическoй суммы конечного числа непрерывных функций равен aлгебpaичecкoй сумме интегралов от слагаемых функций:

5. (Инвариантность формулы интегрирования).

Если   , где u=φ(х) - произвольная функция, имеющая непрерывную производную.▲Пусть х - независимая переменная, ƒ(х) - непрерывная функция и F(x) - ее пepвoобpaзнaя. Тогда

 

 Положим теперь u=ф(х), где ф(х) - непрерывно-дифференцируемая функция. Рассмотрим сложную функцию F(u)=F(φ(x)). В силу инвараинтности формы первого дифференциала функции (см. с. 160) имеем

 

Отсюда    ▼

Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.

12. Метод замены переменной в неопределенном интеграле.

б) Метод подстановки (введение новой переменной)

 

Так как неопределенный интеграл не зависит от выбора аргумента и, учитывая, что

dx = j^/(t)dt,

получаем формулу замены переменной в неопределенном интеграле

. (2.5)

То есть интеграл, стоящий в правой части, может оказаться проще интеграла в левой части.

Пример.

1. .

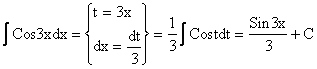2. .

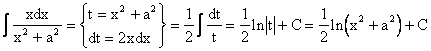3. .

13. Интегрирование по частям в неопределенном интеграле.

в) Метод интегрирования по частям

 

Пусть u и v - непрерывно дифференцируемые функции от х.

d(u×v) = udv + vdu.

Отсюда

udv=d(u×v)-vdu.

 

Интегрируя обе части этого уравнения, получим

или

. (2.6)

Эта формула называется формулой интегрирования по частям.

 

Пример.

1. .

2. .

14. Методы вычисления неопределенных интегралов.

а). Метод разложения.

Пусть f(x) = f₁(x) + f₂(x). Тогда на основании свойства 4

.

f₁, f₂ стараемся подобрать так, чтобы интегралы брались непосредственно.

 

Пример:

1. ?

Воспользуемся .

.

2. =

= .

б). Метод подстановки (введение новой переменной)

 

Так как неопределенный интеграл не зависит от выбора аргумента и, учитывая, что

dx = j^/(t)dt,

получаем формулу замены переменной в неопределенном интеграле

. (2.5)

То есть интеграл, стоящий в правой части, может оказаться проще интеграла в левой части.

Пример.

1. .

2. .

3. .

в) Метод интегрирования по частям

 

Пусть u и v - непрерывно дифференцируемые функции от х.

d(u×v) = udv + vdu.

Отсюда

udv=d(u×v)-vdu.

 

Интегрируя обе части этого уравнения, получим

или

. (2.6)

Эта формула называется формулой интегрирования по частям.

 

Пример.

1. .

2. .

15. Понятие определенного интеграла.

16. Геометрический смысл определенного интеграла.