
Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Чаще всего предполагается (т. н. бинарная или двоичная логика, в отличие от, например, троичной логики), что высказывания могут быть только истинными или ложными.
|
|
Определение
Базовыми
элементами, которыми оперирует алгебра
логики, являются высказывания.
Высказывания строятся над множеством
{B,
![]() ,
,
![]() ,
,
![]() ,
0, 1}, где B — непустое множество, над
элементами которого определены три
операции:
,
0, 1}, где B — непустое множество, над
элементами которого определены три
операции:
отрицание (унарная операция),
конъюнкция (бинарная),
дизъюнкция (бинарная),
а также константы — логический ноль 0 и логическая единица 1.
Дизъю́нкт
— пропозициональная
формула,
являющаяся дизъюнкцией
одного или более литералов
(например
![]() ).
Конъюнкт
— пропозициональная
формула,
являющаяся конъюнкцией
одного или более литералов (например
).
Конъюнкт
— пропозициональная
формула,
являющаяся конъюнкцией
одного или более литералов (например
![]() ).
).
Аксиомы
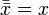 ,
инволютивность
отрицания,
закон
снятия двойного отрицания
,
инволютивность
отрицания,
закон
снятия двойного отрицания




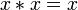
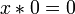

Логические операции
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:
B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь
на этот математический инструментарий,
логика
высказываний
изучает высказывания
и предикаты.
Также вводятся дополнительные операции,
такие как эквивалентность
![]() («тогда
и только тогда, когда»), импликация
(«тогда
и только тогда, когда»), импликация
![]() («следовательно»),
сложение по модулю два
(«следовательно»),
сложение по модулю два
![]() («исключающее
или»),
штрих
Шеффера
(«исключающее
или»),
штрих
Шеффера
![]() ,
стрелка
Пирса
,
стрелка
Пирса
![]() и
другие.
и
другие.
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция приобретает смысл вычитания из единицы; — немодульного сложения; & — умножения; — равенства; — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR); — непревосходства суммы над 1 (то есть A B = (A + B) <= 1).
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.
Свойства логических операций
Коммутативность: x
 y
= y
x,
y
= y
x,
 {&,
{&,
 }.
}.Идемпотентность: x x = x, {&, }.
Ассоциативность: (x y) z = x (y z), {&,
 }.
}.Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
 ,
, ,
,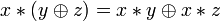 .
.
Законы де Мо́ргана:
 ,
, .
.
Законы поглощения:
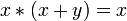 ,
, .
.
Другие (1):
 .
. .
. .
. .
., Инволютивность отрицания, закон снятия двойного отрицания.
Другие (2):
 .
. .
. .
. .
.
Другие (3) (Дополнение законов де Мо́ргана):
 .
. .
.
Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класки
История
Своим существованием наука «алгебра логики» обязана английскому математику Джорджу Булю, который исследовал логику высказываний. Первый в России курс по алгебре логики был прочитан П. С. Порецким в Казанском государственном университете.
АЛГЕБРА ВЫСКАЗЫВАНИЙ является составной частью одного из современных быстро развивающихся разделов математики – математической логики. Математическая логика применяется в информатике, позволяет моделировать простейшие мыслительные процессы. Одним из занимательных приложений алгебры высказываний – решение логических задач.
Объекты алгебры высказываний. Операции над высказываниями. Таблицы истинности. Алгебра – это наука, которая изучает множество некоторых элементов и действия (операции) над ними. Если элементы алгебры – натуральные числа, а операции – сложение и умножение, то это алгебра натуральных чисел. Действия с направленными отрезками (векторами) изучает векторная алгебра.
Объектами алгебры высказываний являются высказывания. Высказывание – это истинное или ложное повествовательное предложение. Повествовательное предложение, в котором говорится об одном-единственном событии, называется простым высказыванием. Например, предложение «Луна – спутник Земли» есть простое высказывание, предложение «Не сорить!» не является высказыванием.
Высказывания обозначаются большими буквами латинского алфавита. Если высказывание A истинно, то пишут A = 1, если ложно, то используют запись A = 0.
Как и в других алгебрах, в алгебре высказываний над ее объектами (высказываниями) определены действия, выполняя которые получают новые высказывания. Объединение двух высказываний в одно при помощи союза «И» называется операцией логического умножения. Полученное таким образом высказывание называется логическим произведением. Например, высказывание A – «В лесу растут грибы», высказывание B – «Льюис Кэрролл – математик», составим произведение этих высказываний AB – «В лесу растут грибы и Льюис Кэрролл – математик». Истинность произведения высказываний зависит от истинности перемножаемых высказываний и может быть определена с помощью следующей таблицы:
А |
В |
АВ |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Объединение двух высказываний в одно с помощью союза «ИЛИ», употребляемого в неисключающем смысле, называется операцией логического сложения. Например, высказывание A – «Декабрь – зимний месяц», В – «Летом иногда идет дождь», определим высказывание A+B – «Декабрь – зимний месяц или летом иногда идет дождь». Установить истинность логической суммы можно с помощью следующей таблицы:
А |
В |
А+В |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
Операция
логического отрицания осуществляется
над одним высказыванием. Выполнить
операцию логического отрицания
(обозначается
![]() )
– значит получить из данного высказывания
новое, присоединяя слова «неверно, что
…» ко всему высказыванию. Истинность
высказывания
)
– значит получить из данного высказывания
новое, присоединяя слова «неверно, что
…» ко всему высказыванию. Истинность
высказывания
![]() определяется
таблицей:
определяется
таблицей:
|
|
1 |
0 |
0 |
1 |
Пользуясь
определенными выше операциями, можно
из простых высказываний образовывать
сложные. Например, всевозможные значения
для высказывания
![]() можно
записать в виде таблицы
можно
записать в виде таблицы
A |
B |
|
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
Тождественные
высказывания. Эквивалентные высказывания.
Формулы Августа де Моргана.
Среди
высказываний особое место занимают те,
в таблице истинности которых либо одни
единицы, либо только нули. Это означает,
что высказывание либо всегда истинно,
либо ложно, независимо от истинности
входящих в него высказываний. Например,
высказывание
![]() всегда
истинно, а высказывание
всегда
истинно, а высказывание
![]() всегда
ложно. Доказать это можно составив
таблицу истинности этих высказываний.
всегда
ложно. Доказать это можно составив
таблицу истинности этих высказываний.
Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными.
Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:
![]() ,
,
![]() .
.
Среди
высказываний встречаются такие, таблицы
истинности которых совпадают. Эти
высказывания называются эквивалентными.
Эквивалентными
являются, например, высказывания
![]() и
и
![]() (то
есть
(то
есть
![]() ).
Это можно проверить составив таблицы
истинности этих высказываний:
).
Это можно проверить составив таблицы
истинности этих высказываний:
A |
B |
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
Операции алгебры высказываний обладают следующими важными свойствами:
Логическое умножение: |
Логическое сложение: |
A·B = B·A |
A + B = B + A |
(AB)C = A(BC) |
(A + B)+ C = A + (B + C) |
A·A = A |
A + A = A |
A·1 = A |
A + 1 = 1 |
A·0 = 0 |
A + 0 = A |
A(B + C) = AB + AC |
A + BC = (A + B)(A + C)A + BC = (A + B)(A + C) |
|
|
Отрицание:
![]()
Формулы, выделенные жирным шрифтом, называются формулами Августа де Моргана (1806–1871). Используя эти формулы, можно, в частности, преобразовывать высказывания: сложные заменять более простыми.
В алгебре высказываний, как и в другой алгебре, возможны тождественные преобразования, но логическое сложение и умножение обладают специфическими свойствами A + A = A, AA = A, A + 1 = A. Это приводит к необычности действий над многочленами алгебры высказываний. Пусть нужно перемножить два сложных высказывания:
(A + B)(A + C) = AA + AC + AB + BC = A + AB + AC + BC.
Рассмотрим теперь два первых слагаемых A + AB = A(1 + B) = A1 = Aи аналогично A+ AC = A. Таким образом, окончательно получаем (A + B)(A + C) = A+ BC.
Преобразование A + AB = A очень часто встречается в алгебре высказываний и называется «поглощение». Есть еще один вид столь же часто встречающегося тождественного преобразования, которое называется «склеивание».
Суть
его состоит в следующем:
![]() (склеивание
произошло по символу B).
Соответственно для сложного высказывания
(склеивание
произошло по символу B).
Соответственно для сложного высказывания
![]() склейку
можно произвести по символу
склейку
можно произвести по символу
![]() ,
то есть имеет место тождественное
преобразование
,
то есть имеет место тождественное
преобразование
![]() .
.
Решение логических задач. Рассмотренных выше законы алгебры высказываний могут быть применены к решению логических задач Например:
Задача:
Алеша, Боря и Гриша откопали древний сосуд. О том, где и когда он был изготовлен, каждый из школьников высказал по два предположения:
Алеша: «Это сосуд греческий и сосуд изготовлен в V веке»;
Боря: «Это сосуд финикийский и сосуд изготовлен в III веке»;
Гриша: «Это не греческий сосуд и изготовлен он в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном их двух своих предположений. Где и в каком веке изготовлен сосуд?
Решение:
Введем обозначения простых высказываний:
«Это
сосуд греческий» –
![]() ;
;
«Это сосуд финикийский» – F;
«Сосуд изготовлен в V веке» – 5;
«Сосуд изготовлен в III веке» – 3;
«Сосуд изготовлен в IV веке» – 4.
Можно
составить формулы высказываний каждого
из школьников с учетом высказывания
учителя. Формула Алешиного высказывания
имеет вид G5.
Учитель сказал, что Алеша прав только
в одном из своих утверждений, поэтому
либо
G =
1, либо 5 = 1. Истинным будет высказывание
![]() ,
то есть высказывание «Сосуд греческий
и изготовлен не в 5 веке или сосуд не
греческий и изготовлен в 5 веке».
Аналогично, высказывание Бори можно
представить формулой
,
то есть высказывание «Сосуд греческий
и изготовлен не в 5 веке или сосуд не
греческий и изготовлен в 5 веке».
Аналогично, высказывание Бори можно
представить формулой
![]() и
высказывание Гриши формулой
и
высказывание Гриши формулой
![]() .
.
Полученные
формулы можно рассматривать как
логические уравнения и решать систему:
![]()
 .
.
Первое высказывание умножается на второе:
![]() .
.
Произведение
![]() –
ложно потому, что сосуд не может быть
изготовлен одновременно в Греции и
Финикии, произведение
–
ложно потому, что сосуд не может быть
изготовлен одновременно в Греции и
Финикии, произведение
![]() –
ложно потому, что сосуд не может быть
изготовлен одновременно в 3 и 5 вв. После
исключения этих высказываний получается
следующее уравнение:
–
ложно потому, что сосуд не может быть
изготовлен одновременно в 3 и 5 вв. После
исключения этих высказываний получается
следующее уравнение:
![]() .
Это уравнение умножается на третье
логическое уравнение составленной
системы:
.
Это уравнение умножается на третье
логическое уравнение составленной
системы:
![]() .
.
Высказывания
![]() исключены
как ложные. Из полученного высказывания
исключены
как ложные. Из полученного высказывания
![]() следует,
что «Сосуд изготовлен в Финикии и сосуд
изготовлен в 5 веке». Это утверждение
согласуется с данными поставленной
задачи.
следует,
что «Сосуд изготовлен в Финикии и сосуд
изготовлен в 5 веке». Это утверждение
согласуется с данными поставленной
задачи.
На примере решения логической задачи продемонстрирована смысловая взаимосвязь входящих в сложное высказывание простых высказываний. В состав сложных высказываний могут входить взаимосвязанные по смыслу высказывания, однако Высказывания могут быть и противоречивыми. Таким образом, одним из применений алгебры высказываний является использование ее для анализа сложных, а подчас противоречивых текстов. Алгебра высказываний позволяет научиться моделировать простейшие мыслительные процессы. «Методы эти позволяют Вам обрести ясность мысли, способность находить собственное оригинальное решение трудных задач, вырабатывают у Вас привычку к систематическому мышлению и, что особенно ценно, умение обнаруживать логические ошибки, изъяны и пробелы тех, кто не пытался овладеть привлекательным искусством логики. Попытайтесь. Вот все, о чем я прошу вас», – Льюис Кэрролл (псевдоним Чарльза Лютвиджа Доджсона
Логические
операции над высказываниями.
1.
ОТРИЦАНИЕ.
Отрицанием
высказывания х
называется новое высказывание, которое
является истинным, если высказывание
х
ложно, и ложным, если высказывание х
истинно.
Отрицание высказывания
х
обозначается
![]() и
читается «не х»
или «неверно, что х».
Логические значения высказывания
можно
описать с помощью таблицы:
и
читается «не х»
или «неверно, что х».
Логические значения высказывания
можно
описать с помощью таблицы:
x |
|
1 |
0 |
0 |
1 |
Таблицы
такого вида принято называть ТАБЛИЦАМИ
ИСТИННОСТИ.
Пусть х
высказывание. Так как
также
является высказыванием, то можно
образовать отрицание высказывания
,
то есть высказывание
![]() ,
которое называется ДВОЙНЫМ ОТРИЦАНИЕМ
высказывания х.
Ясно, что логические значения высказываний
и
х
совпадают.
Например, для высказывания
«Река Волхов вытекает из озера Ильмень»
отрицанием будет высказывание «Неверно,
что река Волхов вытекает из озера
Ильмень» или «Река Волхов не вытекает
из озера Ильмень», а двойным отрицанием
будет высказывание «Неверно, что река
Волхов не вытекает из озера Ильмень».
2.
КОНЪЮНКЦИЯ
(логическое умножение).
Конъюнкцией
двух высказываний x,
y
называется новое высказывание, которое
считается истинным, если оба высказывания
x,
y
истинны, и ложным, если хотя бы одно из
них ложно (т.е. в остальных случаях).
К
,
которое называется ДВОЙНЫМ ОТРИЦАНИЕМ
высказывания х.
Ясно, что логические значения высказываний
и
х
совпадают.
Например, для высказывания
«Река Волхов вытекает из озера Ильмень»
отрицанием будет высказывание «Неверно,
что река Волхов вытекает из озера
Ильмень» или «Река Волхов не вытекает
из озера Ильмень», а двойным отрицанием
будет высказывание «Неверно, что река
Волхов не вытекает из озера Ильмень».
2.
КОНЪЮНКЦИЯ
(логическое умножение).
Конъюнкцией
двух высказываний x,
y
называется новое высказывание, которое
считается истинным, если оба высказывания
x,
y
истинны, и ложным, если хотя бы одно из
них ложно (т.е. в остальных случаях).
К
x |
y |
xy |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
онъюнкция
высказываний x,
y
обозначается символом x&y
или
![]() (xy),
читается «x
и y».
Высказывания x,
y
называются членами конъюнкции. Все
возможные логические значения конъюнкции
двух высказываний x
и y
описываются следующей таблицей
истинности.
Например, для
высказываний «6 делится на 2», «6 делится
на 3» их конъюнкцией будет высказывание
«6 делится на 2 и 6 делится на 3», которое,
очевидно, истинно.
Из определения
операции конъюнкции видно, что союз «и»
в алгебре логики употребляется в том
же смысле, что и в повседневной речи. Но
в обычной речи не принято соединять
союзом «и» два высказывания, далекие
друг от друга по содержанию, а в алгебре
логики рассматривается конъюнкция двух
любых высказываний. (Например: «В огороде
бузина и в Киеве дядька»).
Из
определения операций конъюнкции и
отрицания ясно, что высказывание
(xy),
читается «x
и y».
Высказывания x,
y
называются членами конъюнкции. Все
возможные логические значения конъюнкции
двух высказываний x
и y
описываются следующей таблицей
истинности.
Например, для
высказываний «6 делится на 2», «6 делится
на 3» их конъюнкцией будет высказывание
«6 делится на 2 и 6 делится на 3», которое,
очевидно, истинно.
Из определения
операции конъюнкции видно, что союз «и»
в алгебре логики употребляется в том
же смысле, что и в повседневной речи. Но
в обычной речи не принято соединять
союзом «и» два высказывания, далекие
друг от друга по содержанию, а в алгебре
логики рассматривается конъюнкция двух
любых высказываний. (Например: «В огороде
бузина и в Киеве дядька»).
Из
определения операций конъюнкции и
отрицания ясно, что высказывание
![]() всегда
ложно.
3.
ДИЗЪЮНКЦИЯ
(логическое сложение).
Дизъюнкцией
двух высказываний х,
у
называется новое высказывание, которое
считается истинным, если хотя бы одно
из высказываний х,
у истинно,
и ложным, если они оба ложны.
Дизъюнкция
высказываний х,
у
обозначается символом х
у,
читается «х
или у».
Высказывания х,
у
называются членами дизъюнкции. Все
возможные логические значения дизъюнкции
двух высказываний х
и у
описываются следующей таблицей
истинности:
всегда
ложно.
3.
ДИЗЪЮНКЦИЯ
(логическое сложение).
Дизъюнкцией
двух высказываний х,
у
называется новое высказывание, которое
считается истинным, если хотя бы одно
из высказываний х,
у истинно,
и ложным, если они оба ложны.
Дизъюнкция
высказываний х,
у
обозначается символом х
у,
читается «х
или у».
Высказывания х,
у
называются членами дизъюнкции. Все
возможные логические значения дизъюнкции
двух высказываний х
и у
описываются следующей таблицей
истинности:
x |
y |
xy |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
Например,
высказывание «В треугольнике DFE угол D
или угол E острый истинно, так как
обязательно истинно одно из высказываний:
«В треугольнике DFE угол D острый», «В
треугольнике DFE угол E острый». В
повседневной речи союз «или» употребляется
в различном смысле: исключающем и не
исключающем. В алгебре логики союз «или»
всегда употребляется в не исключающем
смысле.
Из определения операций
дизъюнкции и отрицания ясно, что
высказывание
![]() всегда
истинно.
4.
ИМПЛИКАЦИЯ.
Импликацией
двух высказываний х,
у
называется новое высказывание, которое
считается ложным, если х
истинно, а у
– ложно, и истинным во всех остальных
случаях.
Импликация высказываний
x,y обозначается символом
всегда
истинно.
4.
ИМПЛИКАЦИЯ.
Импликацией
двух высказываний х,
у
называется новое высказывание, которое
считается ложным, если х
истинно, а у
– ложно, и истинным во всех остальных
случаях.
Импликация высказываний
x,y обозначается символом
![]() (или
(или
![]() ),
читается “если х, то y”или ”из х следует
y”. Высказывание х называют УСЛОВИЕМ
или ПОСЫЛКОЙ, высказывание y – СЛЕДСТВИЕМ
или ЗАКЛЮЧЕНИЕМ, высказывание
-
СЛЕДОВАНИЕМ или ИМПЛИКАЦИЕЙ.
Логические
значения операции импликации описываются
следующей таблицей истинности:
),
читается “если х, то y”или ”из х следует
y”. Высказывание х называют УСЛОВИЕМ
или ПОСЫЛКОЙ, высказывание y – СЛЕДСТВИЕМ
или ЗАКЛЮЧЕНИЕМ, высказывание
-
СЛЕДОВАНИЕМ или ИМПЛИКАЦИЕЙ.
Логические
значения операции импликации описываются
следующей таблицей истинности:
x |
y |
x |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Например, высказывание “если число 12 делится на 6, то оно делится на 3”, очевидно, истинно, так как здесь истинна посылка “ Число 12 делится на 6” и истинно заключение “Число 12 делится на 3”.
Употребление слов “если…, то…” в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание “Если х, то y” вообще не имеет смысла. Кроме того, строя предложение вида “ если х, то y” в обыденной речи, мы всегда подразумеваем, что предложение y вытекает из предложения х. Употребление слов “если…, то…” в математической логике не требует этого, поскольку в ней смысл содержания высказываний не рассматривается.
Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме “Если х, то y”. Если при этом известно, что х истинно, и доказана истинность импликации , то мы вправе сделать вывод об истинности заключения y.
5. ЭКВИВАЛЕНЦИЯ.
Эквиваленцией (или эквивалентностью) двух высказываний x,y называется новое высказывание, которое считается истинным, когда оба высказывания x,y либо одновременно истинны, либо одновременно ложны. И ложным во всех остальных случаях.
Эквиваленция высказываний x,y обозначается символом
x |
y |
x↔y |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Например,
эквиваленция “Треугольник SPQ с вершиной
S и основанием PQ равнобедренный тогда
и только тогда, когда
![]() P=
Q”
является истинной, так как высказывания
“Треугольник SPQ с вершиной S и основанием
PQ равнобедренный” и “В треугольнике
SPQ с вершиной S и основанием PQ”
P=
Q”
либо одновременно истинны, либо
одновременно ложны.
Эквивалентность
играет большую роль в математических
доказательствах. Известно, что значительное
число теорем формулируется в форме
необходимых и достаточных условий, т.е.
в форме эквивалентности. В этом случае,
зная об истинности или ложности одного
их двух членов эквивалентности и доказав
истинность самой эквивалентности, мы
делаем заключение об истинности или
ложности второго члена эквивалентности.
P=
Q”
является истинной, так как высказывания
“Треугольник SPQ с вершиной S и основанием
PQ равнобедренный” и “В треугольнике
SPQ с вершиной S и основанием PQ”
P=
Q”
либо одновременно истинны, либо
одновременно ложны.
Эквивалентность
играет большую роль в математических
доказательствах. Известно, что значительное
число теорем формулируется в форме
необходимых и достаточных условий, т.е.
в форме эквивалентности. В этом случае,
зная об истинности или ложности одного
их двух членов эквивалентности и доказав
истинность самой эквивалентности, мы
делаем заключение об истинности или
ложности второго члена эквивалентности.
