Матрицей размерности m x n называется прямоугольная таблица m x n чисел a _ij , i=1,..., m, j=1,..., n:

расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n - порядок матрицы).

• Определение

• Операции с матрицами

:

вычисление определителя

		вычисление определителя умножение матриц вычисление обратной матрицы вычисление ранга матрицы сложение матриц вычитание матриц
a11	a12		...	a1n
a21	a22		...	a2n
...	...		...	...
am1	am2		...	amn

2. n = m

   a11	a12	...	a1n
   ...	...	...	...
   am1	am2	...	amn

3. n ≠ m

   1	0	...	0
   0	1	...	0
   ...	...	...	...
   0	0	...	1
   1	2	...	5
   2	1	...	3
   ...	...	...	...
   5	3	...	1

4. aij = aji

   0	0	...	0
   0	0	...	a
   ...	...	...	...
   0	0	...	0

5. aij = 0

   a11	0	...	0
   0	a22	...	0
   ...	...	...	...
   0	0	...	amn

6. n = m, aii ≠ 0

   a11	0	...	0
   a21	a22	...	0
   ...	...	...	...
   am1	am2	...	amn

7. n = m

   a11	a12	...	a1n
   0	a22	...	a2n
   ...	...	...	...
   0	0	...	amn

8. n = m

9. Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины стробцов.

10. aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

11. Вид матрицы:

12. квадратная

• квадратная

• прямоугольная

• единичная

• симметричная

• нулевая

• диагональная

• треугольная матрица, нижняя

• треугольная матрица, верхняя

Квадратная матрица - это матрица с равным числом столбцов и строк.

1. Сложение и вычитание матриц:

Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицы одинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.

Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами:

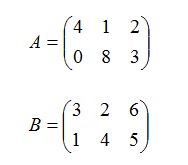
Сумма двух матриц:

Разность двух матриц:

2. Умножение матрицы на число:

Умножение матрицы на число - процесс, заключающийся в умножении числа на каждый элемент матрицы.

Например, пусть дана матрица А:

Умножим число 3 на матрицу А:

3. Умножение двух матриц:

Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы.

Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца.

Можно представить все это в виде схемы:

После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц, можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д.

Посмотрим как это выглядит на схеме:

Посмотрим как это выглядит на примере:

Даны две матрицы:

Найдем произведение этих матриц:

4. Деление матриц:

Деление матриц - действие над матрицами, которое в этом понятии не встретишь в учебниках. Но если есть необходимость разделить матрицу А на матрицу В, то в этом случае используют одно из свойств степеней:

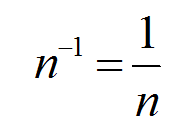
Согласно этому свойству разделим матрицу А на матрицу В:

В результате задача о делении матриц сводиться к умножению обратной матрицы матрице В на матрицу А.

Задачу об обратной матрице рассмотрим в следующей статье.

Итак мы рассмотрели действия над матрицами.

Транспонированная матрица.

Транспонирование матрицы

Над матрицами определена еще одна операция, называемая транспонированием.

Транспонированная матрица обозначается или . Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом -- вторая строка исходной матрицы и т.д. Например,

Транспонирование матриц

Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.

Пример 1. Составить транспонированную матрицу, полученную из А:

Решение: Поменяем местами строки и столбцы, сохраняя порядок:

Обратная матрица

Определение 14 . 8 Матрица называется обратной матрицей для квадратной матрицы , если . Из определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица (иначе одно из произведений или было бы не определено). Обратная матрица для матрицы обозначается . Таким образом, если существует, то . Из определения обратной матрицы следует, что матрица является обратной для матрицы , то есть . Про матрицы и можно говорить, что они обратны друг другу или взаимно обратны.

Предложение 14 . 20 Если матрица имеет обратную, то и . Доказательство . Так как определитель произведения матриц равен произведению определителей ( предложение 14.7 ), то . По следствию 14.1 , поэтому , что невозможно при . Из предыдущего равенства следует также . Последнее предложение можно сформулировать в следующем виде. Если определитель матрицы равен нулю, то обратная к ней не существует. Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения. Определение 14 . 9 Квадратную матрицу назовем вырожденной или особенной матрицей , если , и невырожденной или неособенной матрицей , если . Предложение 14 . 21 Если обратная матрица существует, то она единственна. Доказательство . Пусть две матрицы и являются обратными для матрицы . Тогда и Следовательно, . Предложение 14 . 22 Если квадратная матрица является невырожденной, то обратная для нее существует и ( 14 .14) где -- алгебраические дополнения к элементам . Доказательство . Так как для невырожденной матрицы правая часть равенства ( 14.14 ) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства ( 14.14 ) буквой . Тогда нужно проверить, что и что . Докажем первое из этих равенств, второе доказывается аналогично. Пусть . Найдем элементы матрицы , учитывая, что : Если , то по предложению 14.17 сумма справа равна нулю, то есть при . Если , то 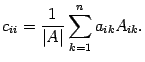Сумма справа представляет собой разложение определителя матрицы по -ой строке ( предложение 14.16 ). Таким образом, 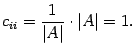Итак, в матрице диагональные элементы равны 1, а остальные равны нулю, то есть . Результаты предложений 14.20 , 14.21 , 14.22 соберем в одну теорему. Теорема 14 . 1 Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица -- невырожденная, обратная матрица единственна, и справедлива формула ( 14.14 ). Замечание 14 . 12 Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца , а второй -- номер строки , в которые нужно записать вычисленное алгебраическое дополнение. Пример 14 . 7 Найдите обратную матрицу для матрицы . Решение. Находим определитель Так как , то матрица -- невырожденная, и обратная для нее существует. 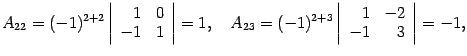Находим алгебраические дополнения: Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй -- строке: ( 14 .15) Полученная матрица и служит ответом к задаче. Замечание 14 . 13 В предыдущем примере было бы точнее ответ записать так: ( 14 .16) Однако запись ( 14.15 ) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде ( 14.15 ) предпочтительнее, если элементы матриц -- целые числа. И наоборот, если элементы матрицы -- десятичные дроби, то обратную матрицу лучше записать без множителя впереди. Замечание 14 . 14 При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку. Пример 14 . 8 Найдите обратную матрицу для матрицы . Решение. -- существует. Ответ: . Нахождение обратной матрицы по формуле ( 14.14 ) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже.