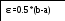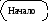Лабораторная работа №1. Безусловная одномерная оптимизация
.docУфимский государственный авиационный технический университет
Лабораторная работа №1
Безусловная одномерная оптимизация
Выполнил студент группы
факультета ИРТ
Проверил:
Хасанов А.Ю.
Уфа 2008
Содержание
1.Цель работы 2
2.Блок схема алгоритмов 3
2.1 Пассивный метод 3
2.2 Блочный метод 4
2.3 Метод золотого сечения 6
2.4 Метод Фибоначчи 8
2.5 Метод деления интервала пополам 9
3.Исходный текст программы 10
4.График функции. 19
5.Вывод. 19
1. Цель работы
Цель работы: знакомство с оптимизационными задачами, изучение различных методов одномерной оптимизации и сравнение эффективности их применения для конкретных целевых функций.
1.1 Постановка задачи одномерной безусловной оптимизации
Поиск экстремума функции одной переменной имеет самостоятельный интерес, так как является составной частью многих методов многомерной оптимизации. От правильной организации одномерного поиска существенно зависит успех решения всей задачи. Кроме того, одномерная оптимизация, будучи простой по формулировке задачей, позволяет легко войти в общую проблематику оптимизационных задач.
Далее будем рассматривать задачу оптимизации на примере задачи минимизации в силу эквивалентности двух типов оптимизационных задач (максимизации и минимизации). Задача поиска минимума целевой функции формулируется в виде:
x*=arg min f(x), xX,
где X – множество допустимых точек, среди которых ищется точка x*, доставляющая минимум f(x) целевой функции.
Когда X=R, мы имеем дело с одномерной безусловной задачей минимизации, т.е. когда целевая функция f(x) имеет только один простой аргумент и область X есть вся вещественная ось чисел.
В методах одномерной оптимизации вместо X=R рассматривается отрезок X=[a,b], содержащей искомое решение x*. Такой отрезок называется отрезком неопределенности, или отрезком локализации. Относительно целевой функции f(x) часто предполагается, что она унимодальная.
1.2 Задание
Решить задачу оптимизации следующими методами одномерной безусловной оптимизации:
- пассивный метод
- метод блочного равномерного поиска;
- метод деления интервала пополам;
- метод золотого сечения;
- метод Фибоначчи.
-
№ варианта
Целевая функция
Отрезок [a,b]
Точность или число экспериментов N
4
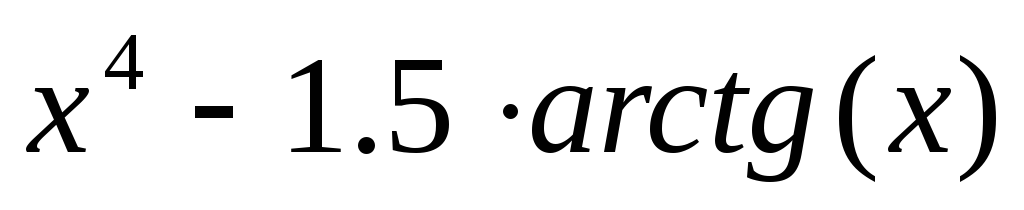
[0,1]
N=21
2.1 Пассивный метод.
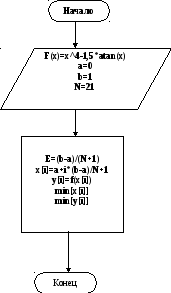
2.2 Алгоритм для блочного метода.
x[0]=a, x[n+1]=b


a=0,b=1,
k=n+1/2,
m=N--1/n-1

h=0


i=1
НЕТ


ДА



y[i]=x[i]*x[i]+exp(x[i]);
i=i+1


min=y[1], f=1


i=1




НЕТ ДА ДА НЕТ НЕТ


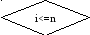



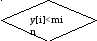



min=y[i],
f=i




i=i+1



a=x[f-1], b=x[f+1], h=h+n

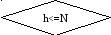




E=(b-a)/2, xp=(a+b)/2, yp=xp*xp+exp(xp) ДА


2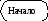
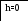

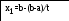

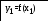

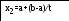

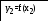






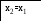



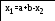

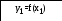

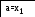
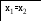

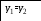

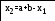




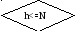












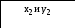

 .3
Метод
золотого сечения.
.3
Метод
золотого сечения.
2.4 Метод Фибоначчи.
2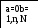
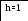

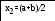
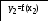


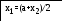
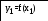

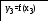





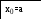
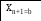



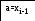


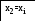




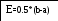

 .5
Метод деления интревала пополам.
.5
Метод деления интревала пополам.





3. Листинг программ
3.1 Программа для пассивного метода.
//1)Для n=2k-1
#include <iostream.h>
#include <math.h>
#include <windows.h>
void main()
{
{
//пункт №1
int i, f, n;
float E, a, b, min, xp, yp, *x, *y;
a=0;
b=1;
cout<<"n =";
cin>>n;
E=(b-a)/(n+1);
x=new float[n+1]; //Пункт №2
y=new float[n+1];
//Пункт №3
for (i=1;i<=n;i++)
{x[i]=a + i*((b-a)/(n+1));
y[i]=x[i]*x[i]*x[i]*x[i]-1.5*atan(x[i]);}
min=y[1];//Пункт №5
f=1;
for (i=1;i<=n;i++)
{ if (y[i]<min) { min=y[i]; f=i;}}
xp=x[f];//Пункт №6
yp=y[f];
cout<<"xp="<<xp<<endl;
cout<<"yp="<<yp<<endl;
cout<<"E="<<E<<endl;
system("pause");
}
}
3.2 Программа для блочного метода.
//1)Для n=2k-1
#include <iostream.h>
#include <math.h>
#include <windows.h>
void main()
{
float a, b;//пункт №1
int i, k, f, n, h, N, m;
float *y, *x, min, E, xp, yp;
a=0;
b=1;
cout<<"N =";
cin>>N;
cout<<"n =";
cin>>n;
k=(n+1)/2; //Пункт №2
x=new float[n+2];
y=new float[n+2];
m=(N-1)/(n-1);
x[k]=(a+b)/2; //Пункт №3
y[k]= x[k]*x[k]*x[k]*x[k]-1.5*atan(x[k]);
h=1;
do
{
x[0]=a;//Пункт №4
x[n+1]=b;
for (i=1;i<=n;i++)
{ x[i]=a + i*((b-a)/(n+1));
y[i]=x[i]*x[i]*x[i]*x[i]-1.5*atan(x[i]); }
min=y[1];//Пункт №5
f=1;
for (i=1;i<=n;i++)
if (y[i]<min) { min=y[i]; f=i;}
a=x[f-1];//Пункт №6
b=x[f+1];
x[k]=x[f];
y[k]=y[f];
h=h+(n-1);
}
while (h<=N); //Пункт №7
E=(b-a)/2;
xp=x[k];
yp=x[k]*x[k]*x[k]*x[k]-1.5*atan(x[k]);
cout<<"xp="<<xp<<endl;
cout<<"yp="<<yp<<endl;
cout<<"E="<<E<<endl;system ("pause");
}
3.3 Программа для метода золотого сечения.
//1)Для n=2
#include <iostream.h>
#include <math.h>
#include <windows.h>
void main()
{
float a, b, t;//пункт №1
int h, N;
float E, xp, yp, x1, y1, x2, y2;
a=0;
b=1;
cout<<"N =";
cin>>N;
t=(1+sqrt(5))/2;
h=0;
x1=a+(b-a)/pow(t,2);
y1=x1*x1*x1*x1-1.5*atan(x1);
x2=a+(b-a)/t;
y2=x2*x2*x2*x2-1.5*atan(x2);
h=h+2;
do
{
if (y1<y2) { b=x2; x2=x1; y2=y1;x1=a+b-x2;
y1=x1*x1*x1*x1-1.5*atan(x1); h=h+1;
}
else { a=x1; x1=x2; y1=y2;
x2=a+b-x1; y2=x2*x2*x2*x2-1.5*atan(x2); h=h+1;
}
}
while (h<=N); //Пункт №7
{if (y1<y2) b=x2;
else a=x1;
xp=(a+b)/2;
yp=xp*xp*xp*xp-1.5*atan(xp);
E=(b-a)/2;
cout<<"xp="<<xp<<endl;
cout<<"yp="<<yp<<endl;
cout<<"E="<<E<<endl;
system ("pause");
}
}
3.4 Прграмма для метода Фибоначчи
#include <iostream.h>
#include <math.h>
#include <windows.h>
void main()
{
float a, b, D, t, *F, x1, x2, y1, y2, xp, yp;//пункт №1
int N, i;
float E;
a=0;
b=1;
cout<<"N =";
cin>>N;
t=(1+sqrt(5))/2;
F=new float[N+1];
F[0]=1;
F[1]=1;
for (i=2;i<=N;i++) F[i]=F[i-1]+F[i-2];
D=(b-a)/(20*F[N]);
x1=a+(b-a)*(F[N-2]/F[N]);
y1=x1*x1*x1*x1-1.5*atan(x1);
x2=a+(b-a)*(F[N-1]/F[N]);
y2=x2*x2*x2*x2-1.5*atan(x2);
for (i=1;i<=(N-3);i++)
{if (y1<y2) { b=x2; x2=x1; y2=y1; x1=a+b-x2; y1=x1*x1*x1*x1-1.5*atan(x1);}
else { a=x1; x1=x2; y1=y2; x2=a+b-x1; y2=x2*x2*x2*x2-1.5*atan(x2);}
}
if (y1<y2) { b=x2; x2=x1; y2=y1;}
else a=x1;
x1=x2-D;
y1=x1*x1*x1*x1-1.5*atan(x1);
if(y1<y2) b=x2;
else a=x1;
xp=(a+b)/2;
yp=xp*xp*xp*xp-1.5*atan(xp);
E=(b-a)/2;
cout<<"xp="<<xp<<endl;
cout<<"yp="<<yp<<endl;
cout<<"E="<<E<<endl;
system ("pause");
}
3.5 Программа для метода деления интервала пополам
//1)Для n=3
#include <iostream.h>
#include <math.h>
#include <windows.h>
void main()
{
float a, b;//пункт №1
int i, h, N, n, f;
float min, E, xp, yp, *x, *y;
a=0;
b=1;
cout<<"N =";
cin>>N;
n=3;
x=new float[n+2];
y=new float[n+2];
x[2]=(a+b)/2;
y[2]=x[2]*x[2]*x[2]*x[2]-1.5*atan(x[2]);
h=1;
do
{
x[1]=(a+x[2])/2;
y[1]=x[1]*x[1]*x[1]*x[1]-1.5*atan(x[1]);
x[3]=(x[2]+b)/2;
y[3]=x[3]*x[3]*x[3]*x[3]-1.5*atan(x[3]);
h=h+2;
x[0]=a;
x[n+1]=b;
min=y[1];
f=1;
for (i=1;i<=n;i++)
if (y[i]<min) { min=y[i]; f=i;}
a=x[f-1];
b=x[f+1];
x[2]=x[f];
y[2]=y[f];
}
while (h<=N); //Пункт №7
E=(b-a)/2;
xp=x[2];
yp=x[2]*x[2]*x[2]*x[2]-1.5*atan(x[2]);
cout<<"xp="<<xp<<endl;
cout<<"yp="<<yp<<endl;
cout<<"E="<<E<<endl;
system ("pause");
}
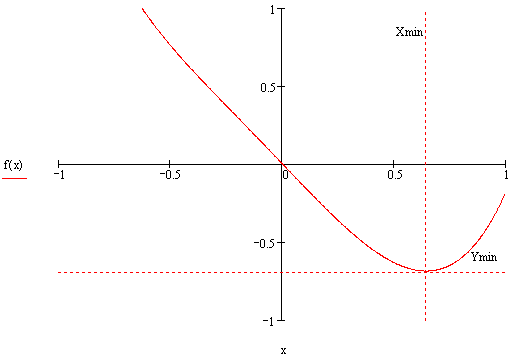
График функции.
4. Вывод
В результате работы программ были получены следующие данные:
Пассивный метод xp=0.636364; yp=-0.686102; E=0.0454545
блочный метод n=21;xp=0.644628;yp=-0.686206;E=00413224
n=3;xp=0.642578;yp=-686218;E=0.000244141
n=5;xp=0.642661;yp=-686218;E=0.000685871
метод золотого сечения xp=0.64306;yp=-0.686218;E=0.000110269
метод Фибоначчи xp=0.642793;yp=-0.686218;E=0.000111669
метод деления интревала пополам xp=0.642578;yp=-0.686218;E=0.000244141
Из этого можно сделать вывод , что метод Фибоначчи является самым оптимальным из предложенных 5 методов.