58. Проверка гипотезы о равенстве математических ожиданий (генеральных средних) двух нормальных распределений.

Пусть имеются две нормально распределенные генеральные совокупности, причем в первой совокупности изучаемый признак X~N(m1;s1), во второй совокупности изучаемый признак Y~N(m2;s2).

Мы в дальнейшем будем рассматривать ситуации, относящиеся к случаям больших выборок из этих двух генеральных совокупностей: n1>30, n2>30. Случаи малых выборок анализируются в соответствующих разделах учебников, но такие ситуации здесь не рассматриваются.

Постановка задачи:

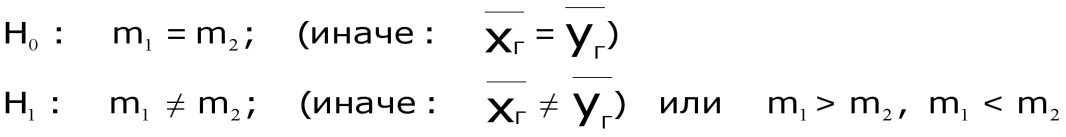
59. Проверка гипотезы о равенстве дисперсий двух нормальных распределений.

Рассмотрим две случайные величины Х и У, каждая из которых подчиняется нормальному закону с дисперсиями . Пусть из этих генеральных совокупностей извлечены две выборки объёмами n1 и n2 . Проверим гипотезу Н0 о том, что относительно альтернативной гипотезы Н1 , заключающейся в том, что

Однако, мы располагаем только выборочными дисперсиями = и = . Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий.

Для построения критической области с выбранной надёжностью необходимо исследовать совместный закон распределения оценок и . Таким законом распределения является распределение Фишера – Снедекора (или F- распределение)

Рассмотрим случайную величину , распределённую нормально с математическим ожиданием Х и с дисперсией . Произведём две независимые выборки объёмами n1 и n2 . Для оценки используют выборочные дисперсии. Случайную величину, определяемую отношением , называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости

, где k1=n1-1, k2=n2-1.

Вернёмся снова к задаче проверки гипотезы о равенстве дисперсий. Сначала нужно вычислить выборочные дисперсии. Найдём отношение F= , причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости и из таблиц находим число F которое сравнивается с вычисленным F. Если окажется, что , то проверяема гипотеза Н0 отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.

60. Проверка гипотезы о равенстве вероятностей (генеральных долей признака) для двух биномиально распределённых генеральных совокупностей.

Рассмотрим две генеральные совокупности.

Из первой генеральной совокупности делается случайная выборка объемом n1, и на основе этой выборки выясняется, сколько объектов выборки обладает изучаемым признаком – этих объектов k1.

Из второй генеральной совокупности делается случайная выборка объемом n2; количество объектов выборки, обладающих изучаемым признаком, - k2.

Выборочные доли признака равны соответственно

w1= k 1 / n1 ; w2= k 2 / n2

В данном пункте мы ограничимся лишь случаем, когда выборки достаточно большие: n1>30, n2>30.

Постановка задачи:

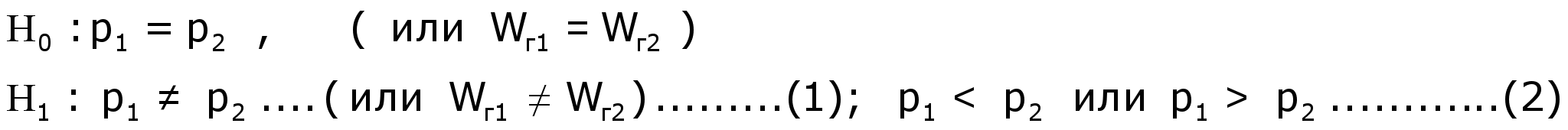
В этой ситуации в качестве критерия используется случайная величина вида

При справедливости гипотезы H0 данная случайная величина имеет стандартный нормальный закон распределения.

61. Предмет корреляционного анализа. Понятие «корреляционная зависимость случайной величины от других переменных». Уравнение и функция регрессии. Предпосылки корреляционного анализа.

Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными.

Предметом корреляционного анализа является выявление

корреляционной связи между признаками.

Корреляционный анализ включает в себя три этапа:

1. выявление наличия корреляционной связи,

2. определение формы корреляционной связи,

3. вычисление тесноты корреляционной связи.

Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

Регрессия - величина, выражающая зависимость среднего значения случайной величины у от значений случайной величины х.

Уравнение регрессии выражает среднюю величину одного признака как функцию другого.

 где f(x) – какая-то неизвестная функция, а   – средняя величина признака, которая изменяется.

f(x) – функция, которая устанавливает вид однозначной зависимости между этими величинами

Функция регрессии - это модель вида у = х, где у - зависимая переменная (результативный признак); х - независимая, или объясняющая, переменная (признак-фактор).

Линия регрессии - график функции у = f (x).

Наиболее часто используются следующие типовые функции: линейная   

параболическая связь  и другие.