
- •Принятые обозначения
- •1. Множества
- •1.1. Операции над множествами
- •1.2. Отображения
- •2. Линейные пространства
- •2.1. Примеры линейных пространств
- •2.2 Размерность, базис, координаты
- •2.2.1 Линейная комбинация и разложение по набору
- •2.2.2 Линейная зависимость
- •2.2.3. Некоторые замечания
- •2.2.4. Размерность и базис
- •2.3. Примеры
- •2.4. Изоморфизм линейных пространств
- •2.5. Подпространства
- •2.6. Примеры подпространств
- •3. Матрицы и определители
- •3.1. Действия над матрицами
- •3.2. Определители
- •3.3. Свойства определителей
- •3.4. Примеры
- •3.5. Обратная матрица
- •3.6. Ранг прямоугольной матрицы
- •4. Линейные операторы
- •4.1. Действия над операторами
- •4.2. Примеры линейных операторов
- •4.3. Линейные уравнения
- •4.4. Матрица линейного оператора
- •4.5. Примеры
- •4.6. Переход к новому базису
- •4.7. Собственные значения и собственные векторы линейного оператора
- •5. Системы линейных уравнений
- •5.1. Случай квадратной матрицы (система порядка n n)
- •5.1.1. Метод обратной матрицы
- •5.1.2. Правило крамера
- •5.1.3. Пример
- •5.2. Метод гаусса. Случай невырожденной квадратной матрицы
- •5.2.1. Прямой ход метода гаусса
- •5.2.2. Обратный ход
- •5.3. Случай прямоугольной матрицы (системы порядка m n)
- •5.3.1. Прямой ход
- •5.3.2. Обратный ход
- •5.4. Пример решения неопределенной системы
- •5.5. Определение ранга матрицы
- •5.6. Нахождение собственных векторов
- •6. Евклидовы пространства и элементы аналитической геометрии
- •6.1. Базисы в евклидовом пространстве
- •6.2. Точки в евклидовом пространстве
- •6.2.1. Сферы и шары
- •6.2.2. Замечание о размерностях
- •6.3. Плоскости в пространстве
- •6.3.1. Неединственность выбора параметров. Каноническая форма уравнения плоскости
- •6.3.2. Геометрический смысл параметров уравнения плоскости
- •6.3.3. Плоскости и линейные функционалы75
- •6.3.4. Сводка формул: плоскость
- •6.4. Прямые в пространстве
- •6.4.1. Геометрический смысл параметров уравнения прямой
- •6.4.2. Прямая, проходящая через две заданные точки
- •6.4.3. Сводка формул: прямая в пространстве
- •6.5. Прямые на плоскости
- •6.6. Векторное и смешанное произведение. Площади и объемы
- •6.6.1. Смешанное произведение и вычисление объемов
- •6.7. Квадратичные формы
- •6.8. Задачи и решения
- •6.8.1. Плоскости и прямые
- •6.8.2. Векторы, длины, объемы
- •6.8.2. Квадратичные формы
2.6. Примеры подпространств
1. В R3 всякая плоскость, проходящая через начало координат, образует двумерное подпространство, а всякая прямая, проходящая через начало координат, образует одномерное подпространство (плоскости и прямые, не содержащие 0, подпространствами быть не могут), и других подпространств в R3 нет.
2.
В пространстве столбцов K3
столбцы вида
![]() ,
т. е. столбцы, у которых третья координата
равна 0, образуют подпространство,
очевидно изоморфное пространству K2
столбцов, высоты 2.
,
т. е. столбцы, у которых третья координата
равна 0, образуют подпространство,
очевидно изоморфное пространству K2
столбцов, высоты 2.
3. В пространстве Pn многочленов, степени не выше n, многочлены, степени не выше 2-х, образуют трехмерное подпространство (у них по три коэффициента).
4. В трехмерном пространстве P2 многочленов, степени не выше 2, многочлены, обращающиеся в 0 в заданной точке х0, образуют двумерное подпространство (докажите!).
5. Задача. В пространстве K4 множество М состоит из столбцов, координаты которых удовлетворяют условию: 1 22 + 3 = 0 (*). Докажите, что М трехмерное подпространство K4.
Решение.
Докажем,
что М
подпространство. Действительно, пусть
аМ,
bМ,
значит, а1
2а2
+ а3
= 0, b1
2b2
+ b3
= 0. Но по правилу сложения векторов (а
+ b)i
= аi
+ bi.
Отсюда следует, что если для векторов
а
и b
условие (*) выполнено, то и для а
+ b
это условие выполнено. Так же ясно, что
если для столбца а
условие (*) выполнено, то оно выполнено
и для столбца а.
И, наконец, нуль-вектор множеству М
принадлежит. Таким образом доказано,
что М
подпространство. Докажем, что оно
трехмерно. Отметим что любой вектор а
М
в силу условия (*) имеет
координаты
 (**). Пусть m1
=
(**). Пусть m1
=
![]() ,
m2
=
,
m2
=
![]() ,
a
h4
=
,
a
h4
=
![]() .
Покажем, что система векторов {m1,
m2,
h4}
образует базис в М.
Составим линейную комбинацию 1m1
+ 2m2
+
h4
=
.
Покажем, что система векторов {m1,
m2,
h4}
образует базис в М.
Составим линейную комбинацию 1m1
+ 2m2
+
h4
=
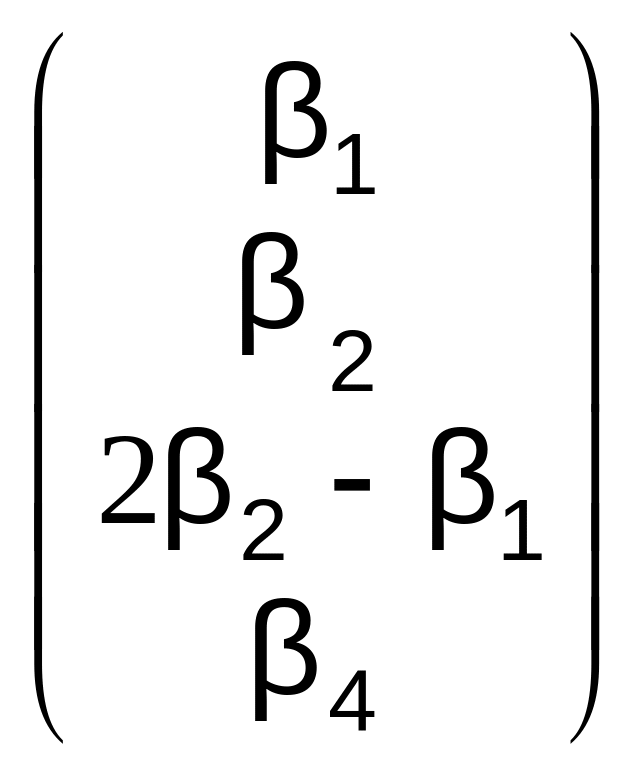 с произвольными коэффициентами. Очевидно,
что любой вектор а
из М
(см. (**)) раскладывается по набору {m1,
m2,
h4};
для этого достаточно выбрать в качестве
коэффициентов разложения координаты
вектора 1
= а1,
2
= а2,
4
= а4.
В
частности, единственной линейной
комбинацией векторов m1,
m2,
h4,
равной нуль-вектору, является комбинация
с нулевыми коэффициентами:
1
= 0,
2
= 0,
4
= 0. Из
единственности разложения нуль-вектора
следует, что {m1,
m2,
h4}
независимая система векторов. А из того
факта, что всякий а
М
раскладывается по системе {m1,
m2,
h4},
следует, что эта система полная. Полная
и независимая система образует базис
в подпространстве М.
Так как этот базис содержит три вектора,
то М
трехмерное подпространство.
с произвольными коэффициентами. Очевидно,
что любой вектор а
из М
(см. (**)) раскладывается по набору {m1,
m2,
h4};
для этого достаточно выбрать в качестве
коэффициентов разложения координаты
вектора 1
= а1,
2
= а2,
4
= а4.
В
частности, единственной линейной
комбинацией векторов m1,
m2,
h4,
равной нуль-вектору, является комбинация
с нулевыми коэффициентами:
1
= 0,
2
= 0,
4
= 0. Из
единственности разложения нуль-вектора
следует, что {m1,
m2,
h4}
независимая система векторов. А из того
факта, что всякий а
М
раскладывается по системе {m1,
m2,
h4},
следует, что эта система полная. Полная
и независимая система образует базис
в подпространстве М.
Так как этот базис содержит три вектора,
то М
трехмерное подпространство.
3. Матрицы и определители
Матрицей
порядка (размерности)
mn
называется прямоугольная таблица,
каждый элемент которой
![]() снабжен двумя индексами: первый указывает
номер строки в матрице, а второй – номер
столбца
снабжен двумя индексами: первый указывает
номер строки в матрице, а второй – номер
столбца
 .
.
Пишут также A = (aij) (1≤ i ≤ m; 1 ≤ j ≤ n); или (aij)mn; указание размера может быть опущено.
Элементами матриц обычно являются вещественные числа, но возможны и матрицы с элементами иной природы, в частности, в качестве элементов матрицы могут выступать другие матрицы.
При
фиксированном первом индексе i
набор элементов (ai1,
ai2,
ai3,
… ain)
называется
i-ой
строкой (например, 3-я строка имеет вид
(a31,
a32,
a33,
… a3n)
),
соответственно, при фиксированном
втором индексе j
набор
![]() называется j-м
столбцом. При n
= m (число
строк равно числу столбцов) матрица
называется квадратной
«порядка n».
называется j-м
столбцом. При n
= m (число
строк равно числу столбцов) матрица
называется квадратной
«порядка n».
Совокупность элементов квадратной матрицы {aii} = {a11 a22 … ann} с одинаковым номером строки и столбца называется главной диагональю. Если у квадратной матрицы все элементы равны нулю, кроме элементов aii, стоящих на главной диагонали, матрица называется диагональной; если равны нулю все элементы, ниже главной диагонали (k < i aik = 0), матрица называется верхней треугольной (если равны нулю все элементы выше главной диагонали – то нижней треугольной).
Если все диагональные элементы диагональной матрицы равны единице, матрица называется единичной и обозначается E:
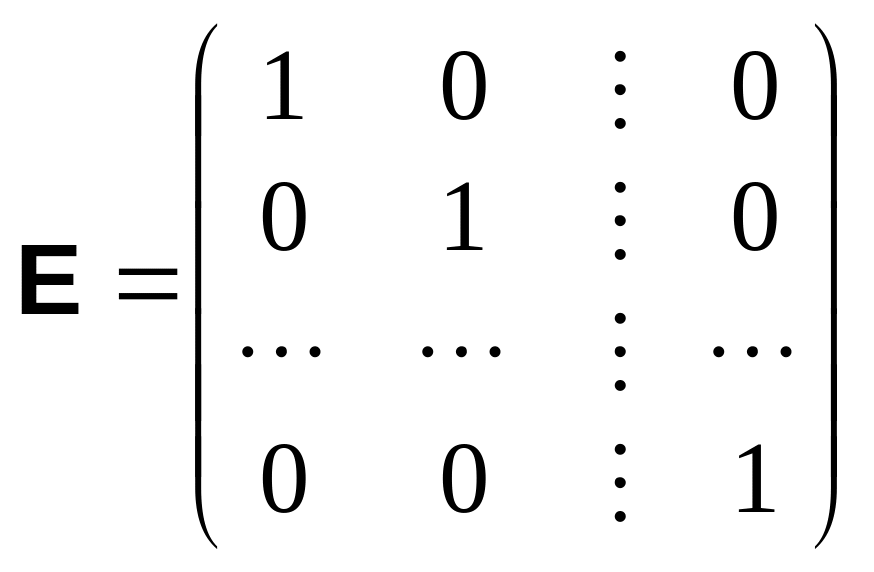 .
.
Транспонированием (транспозицией) матрицы называется замена в мат-рице строк столбцами и наоборот; соответственно, у равных элементов пря-мой и транспонированной матриц меняются местами индексы17. При записи операция транспозиции обозначается штрихом справа вверху (aik)' = (aki).
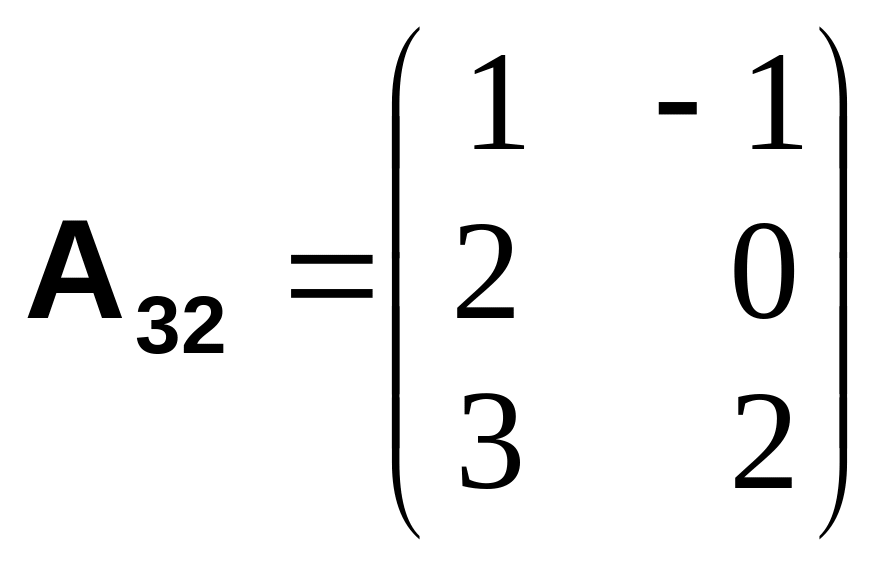
![]()
