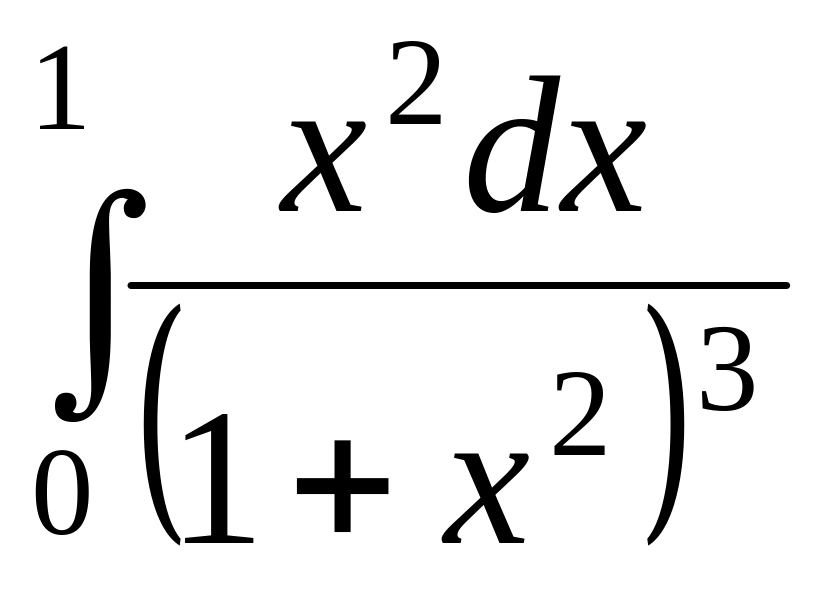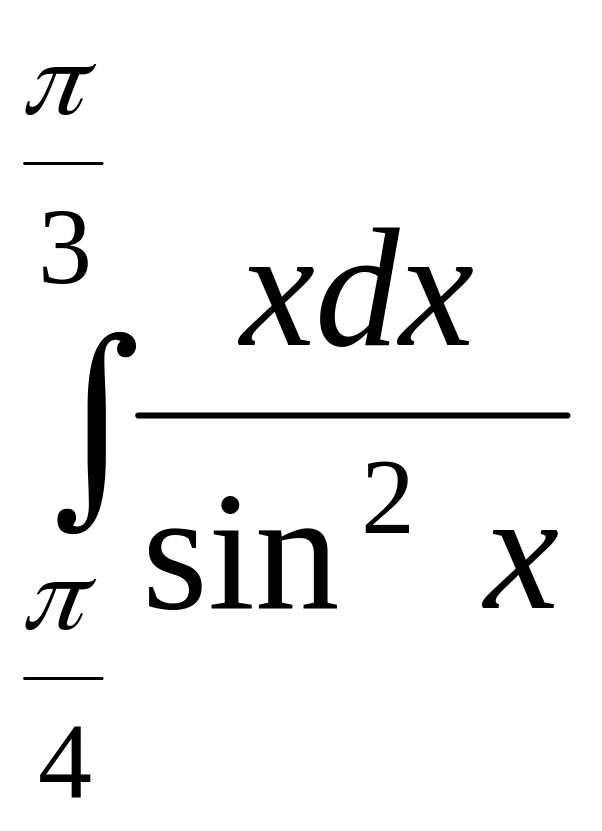Замена переменной в определенном интеграле

ЛИТЕРАТУРА [5], ч.1, гл.10,§ 7, п.3; [6] п. 20.1

Если функция непрерывна на отрезке функция, непрерывная вместе со своей производной на отрезке причем определена и непрерывна на отрезке то

Для преобразования подынтегрального выражения используются те же подстановки, что и для неопределенного интеграла.

Пример 1. Вычислить интеграл

Решение. Делаем замену находим новые пределы интегрирования:

Пример 2. Вычислить интеграл

Решение. Делаем замену тогда находим новые пределы интегрирования:

Задачи:

Найти интегралы:

1).	2).
3).	4).
5).	6).
7).	8).
9).	10).

Интегрирование по частям

ЛИТЕРАТУРА: [5],ч.1, гл.10,§ 7,п.4; [6] п. 30.2

Если функции непрерывно дифференцируемы на отрезке , то

Пример 1. Вычислить интеграл .

Решение.

Пример 2. Вычислить интеграл

Решение.

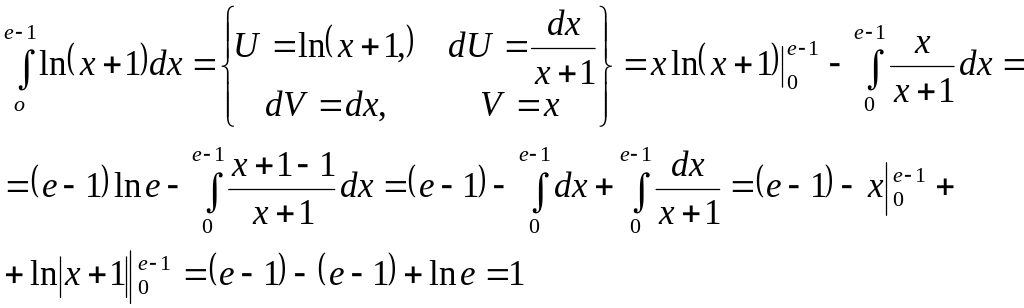
Задачи:

Найти интегралы:

1).	2).
3).	4).
5).	6).
7).	8).

Приложения определенного интеграла

ЛИТЕРАТУРА: [5] ч.1, гл.11; [6] § 32.

1. Площадь плоской фигуры. Прямоугольная система координат.

Если непрерывная кривая задана в прямоугольной системе координат уравнением , где , то площадь криволинейной трапеции, ограниченной этой кривой, двумя прямыми и отрезком оси абсцисс определяется формулой

В более общем случае, если площадь S ограничена двумя непрерывными кривыми и двумя вертикальными линиями при то площадь вычисляется по формуле:

Если кривая задана уравнением в параметрической форме то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальными линиями и отрезком оси ОХ, выражается интегралом

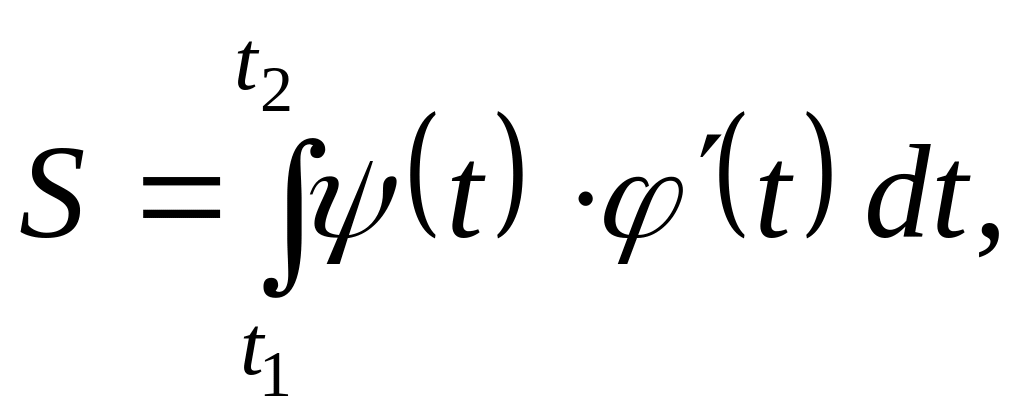
где определяются из уравнений

Пример 1. Вычислить площадь фигуры, ограниченной параболами

Решение. Построим заданные линии.

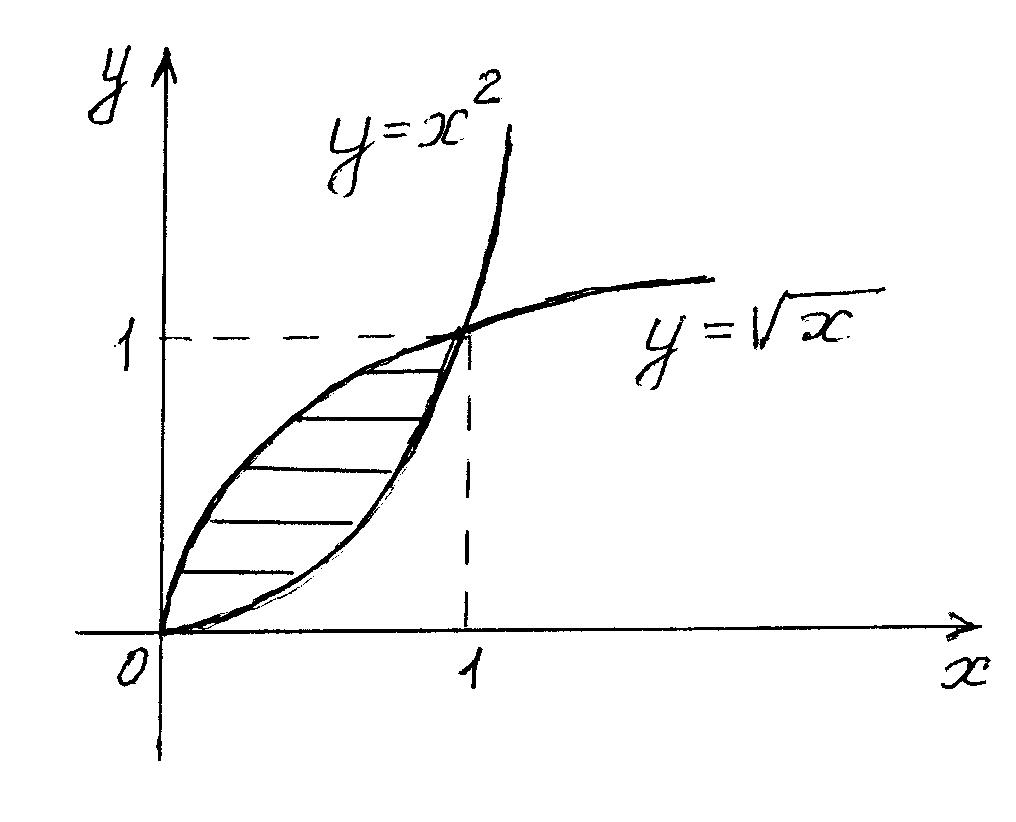
( кв. ед.).

Пример 2. Найти площадь фигуры, ограниченной одной аркой циклоиды и осью абсцисс.

Решение. Построим область интегрирования.

Если . С учетом того, что получим

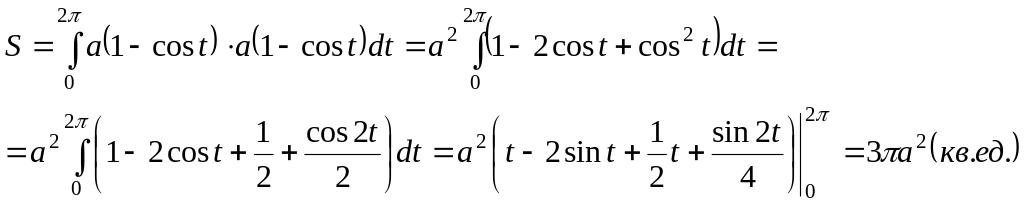
Пример3. Вычислить площадь фигуры, ограниченной линиями

Решение. Построим область интегрирования и разобьем ее на подобласти. Тогда

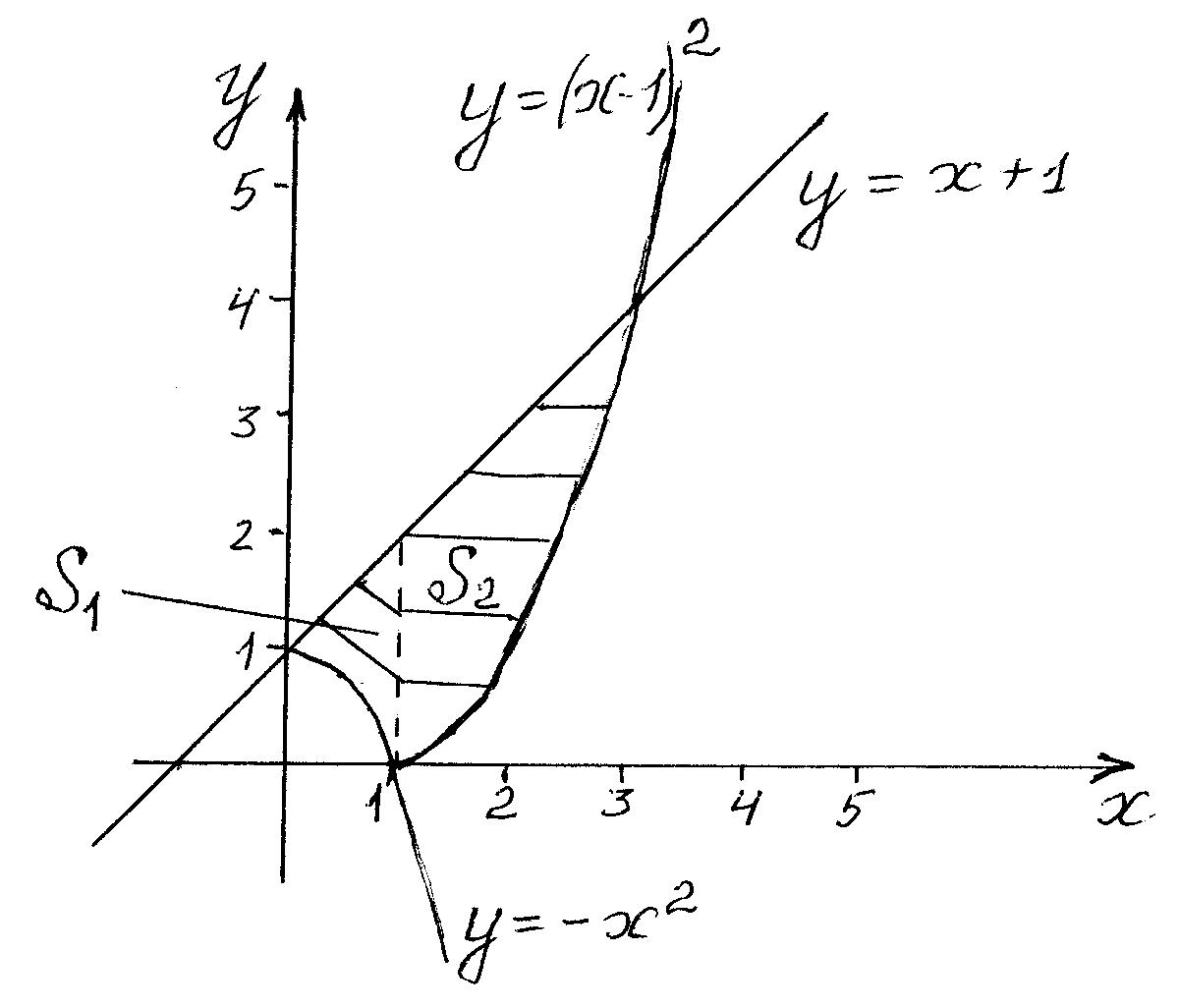
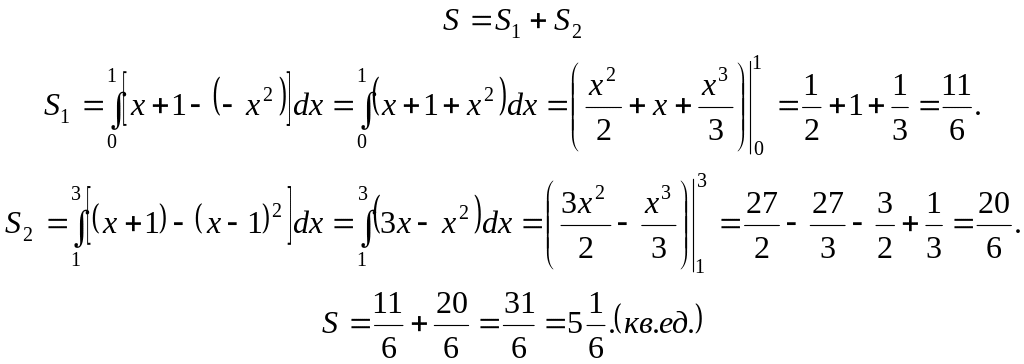
Пример 4. Вычислить площадь фигуры, ограниченной линиями

Решение. Построим область интегрирования.

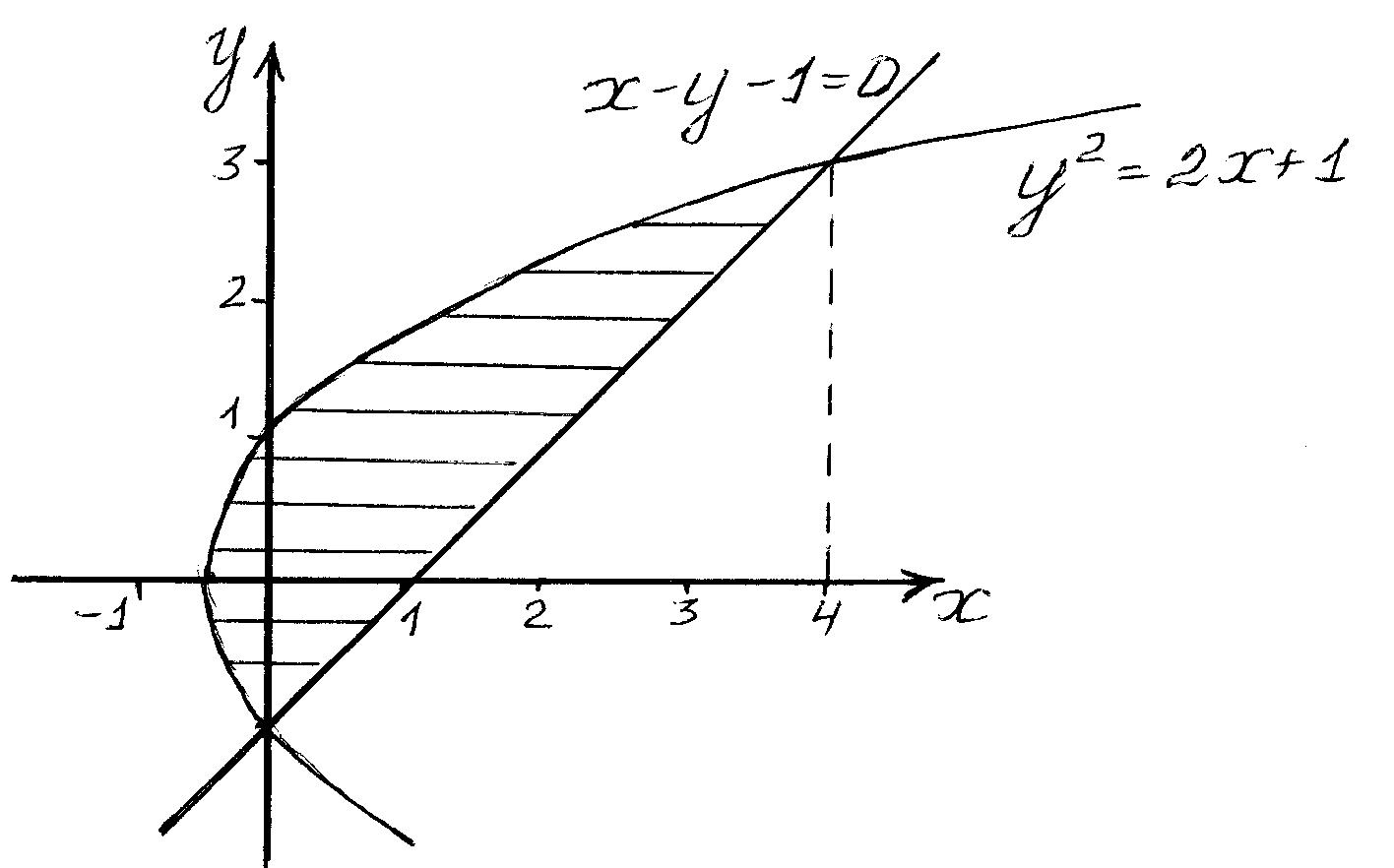
Площадь полученной фигуры удобнее вычислять, если рассматривать ее относительно оси OY. Пусть y – независимая переменная. Уравнения параболы и прямой запишем в виде . Тогда

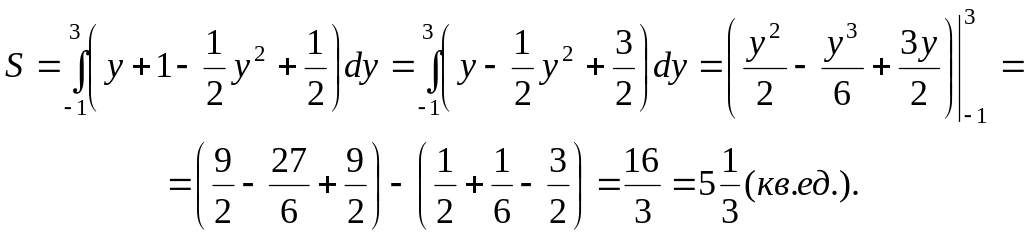
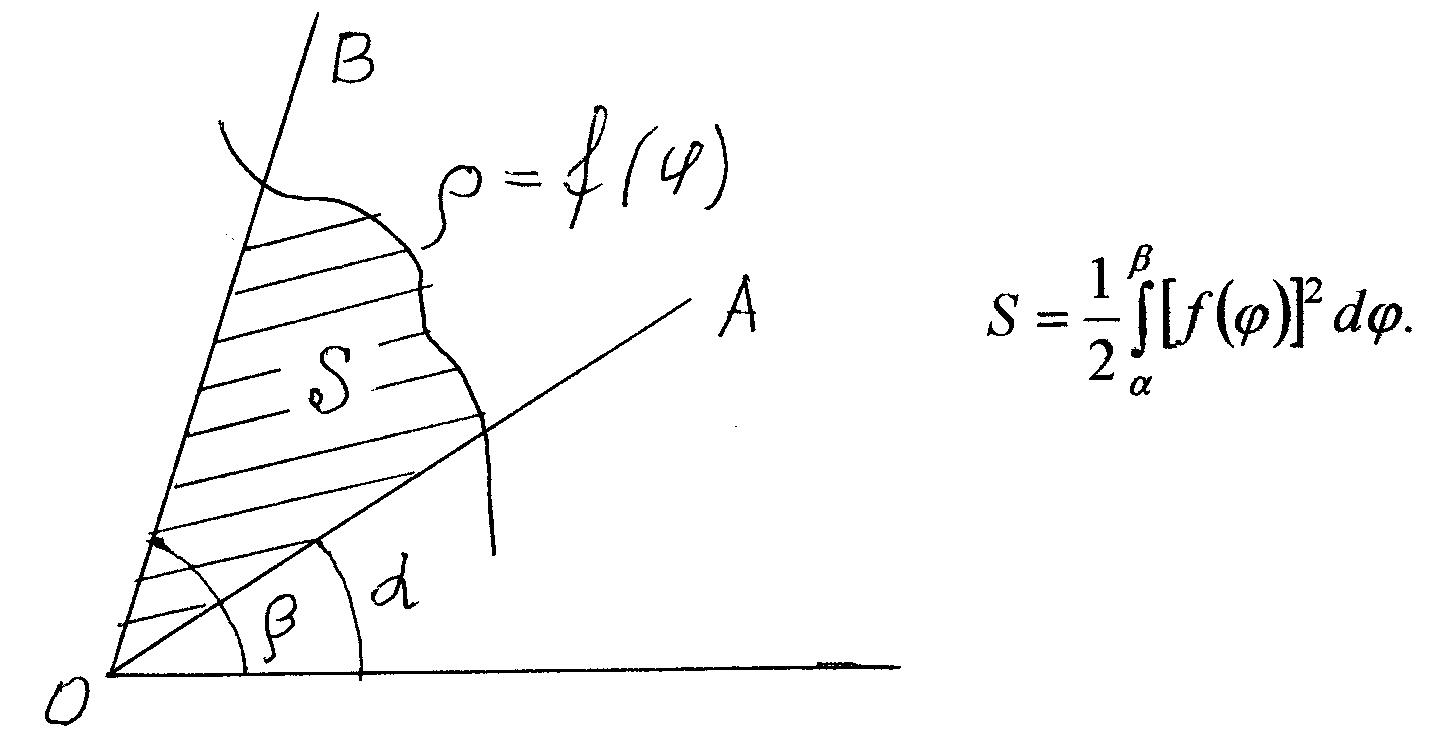
2. Площадь плоской фигуры. Полярная система координат.

Если непрерывная кривая задана в полярной системе координат уравнением то площадь сектора АОВ, ограниченного дугой кривой и двумя полярными радиусами ОА и ОВ, соответствующими значениям , выразится интегралом

Пример 5. Найти площадь фигуры, ограниченной линией (двухлепестковая роза).

Решение. Придавая последовательно приращения углу построим график кривой.

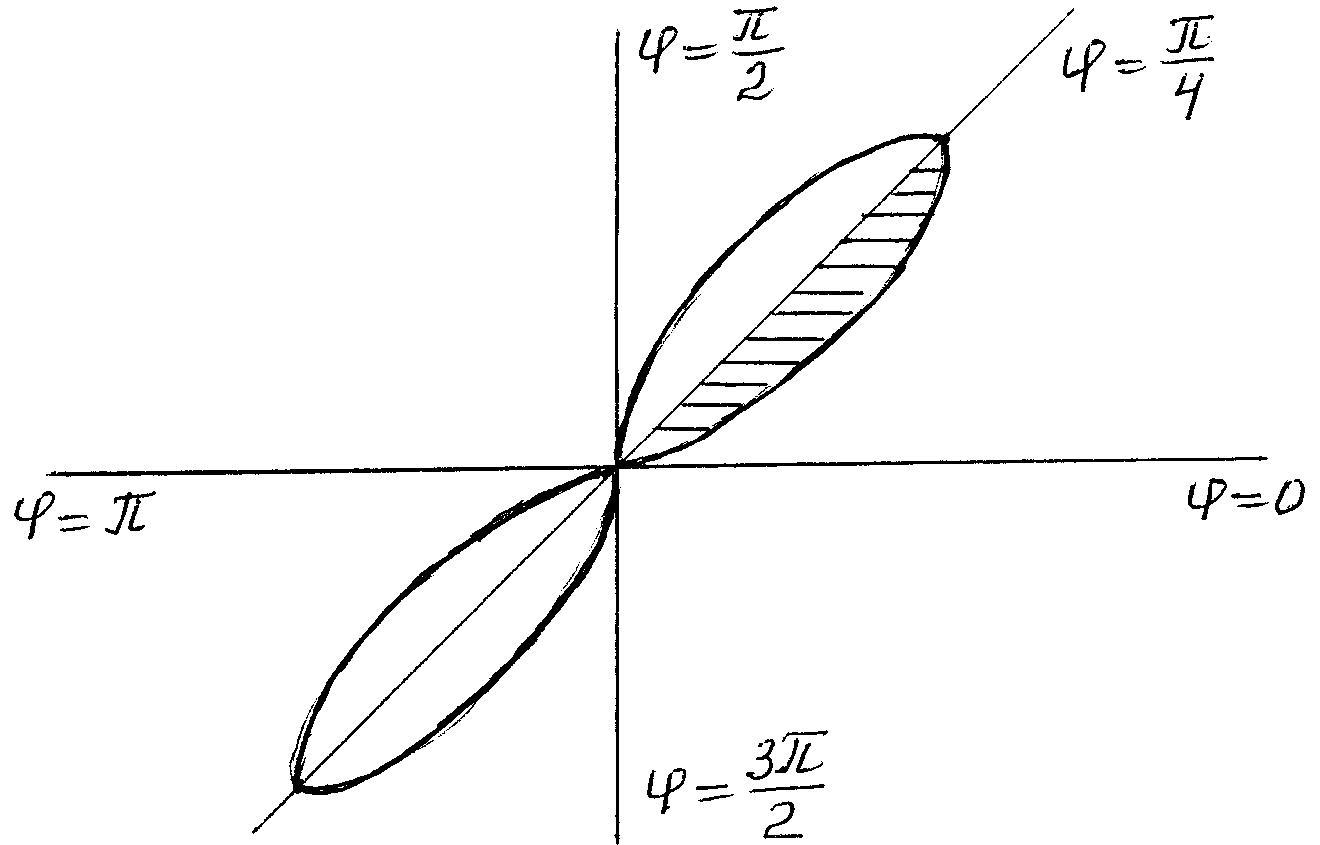
С учетом симметричности фигуры искомая площадь равна

3. Длина дуги кривой.

а) В прямоугольной системе координат.

Длина l дуги гладкой кривой содержащейся между двумя точками с абсциссами равна

б) Заданной параметрически.

Если кривая задана параметрически уравнениями , где непрерывно дифференцируемые функции, то длина дуги l кривой равна

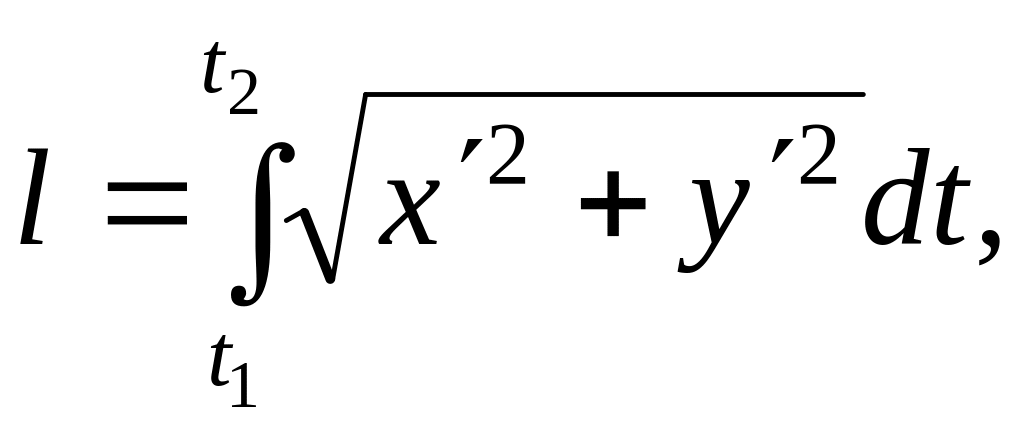
где значения параметра, соответствующие концам дуги

в) В полярной системе координат.

Если гладкая кривая задана в полярной системе координат уравнением то длина дуги l равна

где значения полярного угла в крайних точках дуги

Пример 6. Найти длину петли линии

Решение. Приравнивая y к нулю получим, что С учетом того, что получаем:

4. Объем тела вращения.

Объем тел , образованных вращением криволинейной трапеции, ограниченной кривой осью OX и двумя вертикальными прямыми вокруг оси OX и OY, выражаются формулами

Если кривая задана в иной форме (параметрически, в полярных координатах и т.д.), то в приведенных формулах нужно сделать соответствующую замену переменной интегрирования.

В более общем случае, объемы тел, образованных вращением фигуры, ограниченной кривыми и прямыми x = a, x = b вокруг координатных осей OX, OY соответственно равны:

Пример 7. Фигура, ограниченная гиперболой и прямой вращается вокруг оси абсцисс. Найти объем тела вращения.

Решение. Из чертежа и условия получаем

Объем тела, полученного при вращении сектора, ограниченного дугой кривой и двумя полярными радиусами вокруг полярной оси, может быть вычислен по формуле:

5. Площадь поверхности вращения.

Площадь поверхности, образованной вращением вокруг оси OX дуги гладкой кривой заключенной между точками выражается формулой:

где дифференциал дуги кривой.

Т.е.

Если дуга задана параметрическими уравнениями то

Если дуга задана в полярных координатах , то

Пример 8. Найти площадь поверхности, образованной вращением вокруг оси OX дуги кривой

Решение.

В силу симметрии фигуры