Кафедра прикладной математики

ПРАКТИКУМ № 5.

ТЕМА: ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПРИКЛАДНЫХ ЗАДАЧ СРЕДСТВАМИ ТАБЛИЧНОГО РЕДАКТОРА EXCEL.

Цель работы: приобретение практических навыков в реализации численных методов решения практических задач с помощью табличного редактора Excel.

1. Аппроксимация экспериментальных данных Постановка задачи

Пусть величина y является функцией аргумента x. Это означает, что любому значению x из области определения поставлено в соответствие значение y. Вместе с тем на практике часто неизвестна явная связь между y и x, т.е. невозможно записать эту связь в виде некоторой зависимости y=f(x). В некоторых случаях даже при известной зависимости y=f(x) она настолько громоздка (содержит трудно вычисляемые выражения, сложные интегралы), что ее использование в практических расчетах затруднительно.

Наиболее распространенным и практически важным случаем, когда вид связи между параметрами x и y неизвестен, является задание этой связи в виде некоторой таблицы {x_i, y_i}. Это означает, что дискретному множеству значений аргумента {x_i} поставлено в соответствие множество значений функций {y_i} (i=0, 1, … , n). Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике могут попадаться значения величины y и в других точках, отличных от узлов x_i. Однако получить эти значения можно лишь путем очень сложных расчетов.

Следовательно, с точки зрения экономии времени и средств необходимо использовать имеющиеся табличные данные для приближенного вычисления искомого параметра y при любом значении (из некоторой области) определяющего параметра x, т.к. точная связь y=f(x) неизвестна.

Этой цели и служит задача о приближении (аппроксимации) функций: данную функцию f(x) требуется приближенно заменить (аппроксимировать) некоторой функцией так, чтобы отклонение (в некотором смысле) от f(x) в заданной области было наименьшим. Функция называется аппроксимирующей.

Для практики весьма важен случай аппроксимации функции многочленом

(1.1)

В дальнейшем будем рассматривать лишь такого рода аппроксимацию. При этом коэффициенты a_j будут подбираться так, чтобы достичь наименьшего отклонения многочлена от данной функции.

Если приближение строится на заданном дискретном множестве точек {x_i}, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение. При построении приближения на непрерывном множестве точек (на отрезке [a,b]) аппроксимация называется непрерывной (или интегральной).

Точечная аппроксимация

Одним из основных типов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции y=f(x) строится многочлен (1.1), принимающий в заданных точках x_i те же значения y_i, что и функция f(x), т.е.

(1.2)

При этом предполагается, что среди значений x_i нет одинаковых, т.е. при . Точки x_i называются узлами интерполяции, а многочлен – интерполяционным многочленом.

Таким образом, близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек. Максимальная степень интерполяционного многочлена m=n; в этом случае говорят о глобальной интерполяции, поскольку один многочлен

(1.3)

используется для интерполяции функции f(x) на всем рассматриваемом интервале изменения аргумента x. Коэффициенты a_j многочлена (1.3) находятся из системы уравнений (1.2), которая при ( ) имеет единственное решение.

И нтерполяционные многочлены могут строиться отдельно для разных частей рассматриваемого интервала изменения x. В этом случае имеем кусочную (локальную) интерполяцию. Как правило, интерполяционные многочлены используются для аппроксимации функции в промежуточных точках между крайними узлами интерполяции, т.е. при x₀<x<x_n. Однако иногда они используются и для приближенного вычисления функции вне рассматриваемого отрезка (x<x₀; x>x_n). Это приближение называется экстраполяцией.

Линейная и квадратичная интерполяции

Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точки (x_i, y_i) (i=0, 1, 2, … , n) соединяются прямолинейными отрезками, и функция f(x) приближается ломанной с вершинами в данных точках. Уравнения каждого отрезка ломанной в общем случае разные. Поскольку имеется n интервалов (x_i-1, x_i), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки (x_i-1, y_i-1) и (x_i, y_i), в виде

.

Отсюда (1.4)

Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (1.4) и найти приближенное значение функции в этой точке. Блок-схема данного алгоритма приведена.

Задание: будет ли работать алгоритм по данной блок-схеме, если окажется, что x<x₀ или x>x_n?

Рассмотрим случай квадратичной интерполяции. В качестве интерполяционной функции на отрезке [x_i-1, x_i+1] принимается квадратичный трехчлен. Такую интерполяцию называют еще параболической. Уравнение квадратного трехчлена

(1.5)

содержит три неизвестных коэффициента a_i, b_i, c_i для определения которых необходимы три уравнения. Ими служат условия прохождения параболы (1.5) через три точки (x_i-1, y_i-1), (x_i, y_i), (x_i+1,y_i+1). Эти условия можно записать в виде

(1.6)

Интерполяция для любой точки проводится по трем ближайшим к ней узлам.

Пример:

Найти приближенное значение функции y=f(x) при x = 0,32, если известна следующая таблица ее значений:

X	0,15	0,3	0,4	0,55
y	2,17	3,63	5,07	7,78

Решение:

Воспользуемся сначала формулой линейной интерполяции (1.4). Значение x=0,32 находится между узлами x_i-1 = 0.3 и x_i = 0.4. Имеем

Найдем теперь приближенное значение функции с помощью формулы квадратичной интерполяции (1.5). Составим систему уравнений (1.6) с учетом ближайших к точке x = 0,32 узлов:

x_i-1=0,15; x_i=0,3; x_i+1=0,4. Соответственно, y_i-1=2,17; y_i=3,63; y_i+1=5,07. Система будет иметь вид:

Решая эту систему, находим a_i=18,67; b_i=1,33; c_i=1,55. Искомое значение функции

.

При интерполировании основным условием является прохождение графика интерполяционного многочлена через данные значения функции в узлах интерполяции. Однако в ряде случаев выполнение этого условия затруднительно или даже нецелесообразно. Например, при большом количестве узлов интерполяции получается высокая степень многочлена в случае глобальной интерполяции, т.е. когда нужно иметь один интерполяционный многочлен для всего интервала изменения аргумента. Кроме того, табличные данные могли быть получены путем измерений и содержать ошибки. Во многих случаях, особенно при обработке экспериментальных данных, среднеквадратичное приближение функций с помощью многочлена (1.1) вполне приемлемо, поскольку оно сглаживает некоторые неточности функции f(x) и дает достаточно правильное представление о ней. На практике стараются подобрать аппроксимирующий многочлен как можно меньшей степени (как правило, m = 1, 2, 3).

АППРОКСИМАЦИЯ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Мерой отклонения многочлена от заданной функции f(x) на множестве точек (x_i, y_i) (i=0, 1, 2, … , n) при среднеквадратичном приближении является величина S, равная сумме квадратов разностей между значениями многочлена и функции в данных точках:

(1.7)

Для построения аппроксимирующего многочлена нужно подобрать коэффициенты a₀, a₁, … , a_m так, чтобы величина S была наименьшей. В этом и состоит метод наименьших квадратов. В теории вероятностей доказывается, что полученные таким методом значения параметров наиболее вероятны, если отклонения подчиняются нормальному закону распределения.

Поскольку здесь параметры a₀, a₁, … , a_m выступают в роли независимых переменных функции S, то ее минимум найдем, приравнивая нулю частные производные по этим переменным:

(1.8)

Полученные соотношения – система уравнений для определения a₀, a₁, … , a_m.

Рассмотрим применение метода наименьших квадратов для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим многочлен (1.1). Формула (1.7) для определения суммы квадратов отклонений S примет вид:

(1.9)

Для составления системы уравнений (1.8) найдем частные производные функции :

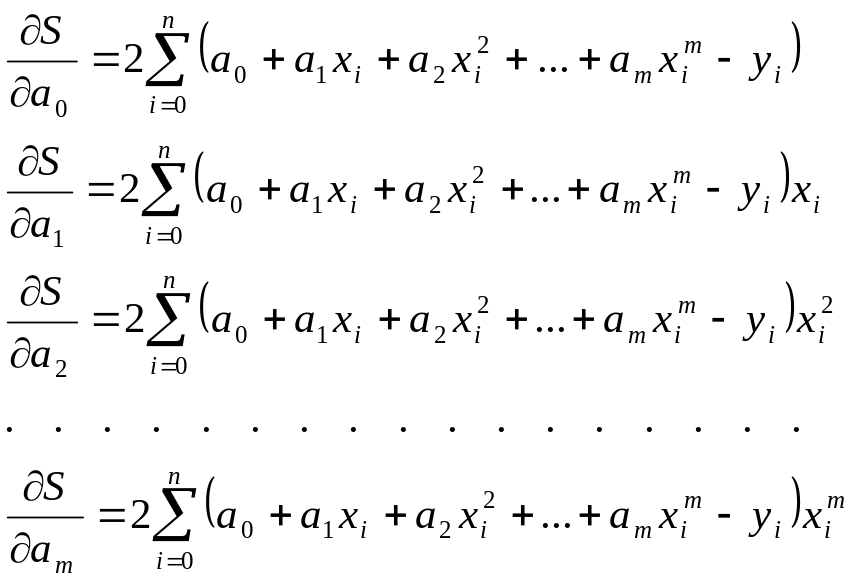
Приравнивая эти выражения нулю в соответствии с уравнениями (1.8) и собирая коэффициенты при неизвестных a₀, a₁, … , a_m получаем следующую систему уравнений:

(1.10)

Решая эту систему линейных уравнений, получаем коэффициенты a₀, a₁, … , a_m многочлена (1.1), которые являются искомыми параметрами эмпирической формулы.

Пример:

Используя метод наименьших квадратов, вывести эмпирическую формулу для функции y=f(x) заданной в табличном виде:

x	0,75	1,5	2,25	3,0	3,75
y	2,5	1,2	1,12	2,25	4,28

Решение:

Если изобразить данные табличные значения на графике, то видно, что в качестве эмпирической формулы для аппроксимации функции y=f(x) можно принять квадратный трехчлен:

.

В данном случае имеем m=2, n=4, и система уравнений (1.10) примет вид:

Расчет по накоплению сумм удобно вести в таблице:

i	xi	xi^2	xi^3	xi^4	yi	xiyi	xi^2yi
0	0,75	0,5625	0,421875	0,316406	2,5	1,875	1,40625
1	1,5	2,25	3,375	5,0625	1,2	1,8	2,7
2	2,25	5,0625	11,39063	25,62891	1,12	2,52	5,67
3	3	9	27	81	2,25	6,75	20,25
4	3,75	14,0625	52,73438	197,7539	4,28	16,05	60,1875
	11,25	30,9375	94,92188	309,7617	11,35	28,995	90,21375

Система уравнений запишется в виде:

Решая систему уравнений, находим значения параметров эмпирической формулы:

Таким образом, получаем следующую аппроксимацию функции, заданной в табличной форме:

.

РАВНОМЕРНОЕ ПРИБЛИЖЕНИЕ

Иногда при построении приближения ставится более жесткое условие: требуется, чтобы во всех точках некоторого отрезка [a,b] отклонение многочлена от функции f(x) было по абсолютной величине меньшим заданной величины В этом случае говорят, что многочлен равномерно аппроксимирует функцию f(x) с точностью на отрезке [a,b].

Введем понятие абсолютного отклонения многочлена от функции f(x) на отрезке [a,b]. Оно равно максимальному значению абсолютной величины разности между ними на данном отрезке . По аналогии можно ввести понятие среднеквадратичного отклонения при среднеквадратичном приближении функций.

Возможность построения многочлена, равномерно приближающего данную функцию, следует из теоремы Вейерштрасса об аппроксимации:

Если функция f(x) непрерывна на отрезке [a,b], то для любого существует многочлен степени абсолютное отклонение которого от функции f(x) на отрезке [a,b] меньше .

Существует понятие наилучшего приближения функции f(x) многочленом фиксированной степени m. В этом случае коэффициенты многочлена следует выбирать так, чтобы на заданном отрезке [a,b] величина абсолютного отклонения была минимальной. Многочлен называется многочленом наилучшего равномерного приближения. Существование и единственность многочлена наилучшего равномерного приближения вытекает из следующей теоремы:

Для любой функции f(x), непрерывной на замкнутом ограниченном множестве G, и любого натурального m, абсолютное отклонение которого от функции f(x) минимально, т.е. , причем такой многочлен единственный.

Множество G обычно представляет собой либо некоторый отрезок [a,b], либо конечную совокупность точек x₀, x₁, x₂, …, x_n.

ИСПОЛЬЗОВАНИЕ ТАБЛИЧНОГО РЕДАКТОРА EXCEL ДЛЯ РЕШЕНИЯ ЗАДАЧ

АППРОКСИМАЦИИ

ПРИМЕР 1.

Таблица содержит данные о величине прогиба консольной балки с грузом на конце в зависимости от расстояния от закрепленного конца.

Расстояние (дюймы)	Прогиб (дюймы)
0	0,0000
12	0,0245
24	0,0951
36	0,2077
48	0,3581
60	0,5420
72	0,7553
84	0,9938
96	1,2533
108	1,5295
120	1,8184
132	2,1156
144	1,4170

Необходимые вычисления удобно выполнить, пользуясь таблицей, где используются следующие клеточные формулы:

D4=B4*C4, E4=B4^2, G4=C4^2, F4=E$2+D$2*B4,

D2=(СЧЕТ(B4:B13)*D14-B14*C14)/(СЧЕТ(B4:B13)*E14-B14*B14),

E2=(C14-D2*B14)/СЧЕТ(B4:B13),

G2=(СЧЕТ(B4:B13)*$D$14-$B$14*C14)/(КОРЕНЬ(СЧЕТ(B4:B13)*$E$14-

B14*B14)*КОРЕНЬ(СЧЕТ(B4:B13)*$G$14-$C$14*$C$14)).

	A	B	C	D	E	F	G
1	УРАВНЕНИЕ РЕГРЕССИИ
2	Y=a+bx=			0,014679	-0,20x	R=	0,951447
3	I	xi	yi	xi*yi	X^2	Yрасч.	y^2
4	1	0	0,0000	0	0	-0,2022	0,0000
5	2	12	0,0245	0,294	144	-0,0261	0,0006
6	3	24	0,0951	2,2824	576	0,1501	0,0090
7	4	36	0,2077	7,4772	1296	0,3262	0,0431
8	5	48	0,3581	17,1888	2304	0,5024	0,1282
9	6	60	0,542	32,52	3600	0,6785	0,2938
10	7	72	0,75553	54,39816	5184	0,8547	0,5708
11	8	84	0,9938	83,4792	7056	1,0308	0,9876
12	9	96	1,2533	120,3168	9216	1,2069	1,5708
13	10	108	1,5295	165,186	11664	1,3831	2,3394
14	11	120	1,8184	218,208	14400	1,5592	3,3066
15	12	132	2,1156	279,2592	17424	1,7354	4,4758
16	13	144	1,417	204,048	20736	1,9115	2,0079
17	Σ	936	11,1105	1184,658	93600		15,7336

В Excel аппроксимация экспериментальных данных осуществляется путем построения их графика (х – отвлеченные величины) или точечного графика (х – имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции (линии тренда). Возможны следующие варианты функций:

1. Линейная – . Обычно применяется в простейших случаях, когда экспериментальные данные возрастают или убывают с постоянной скоростью.

2. Полиномиальная – , где до шестого порядка включительно ( ), ai – константы. Используя для экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени – не более трех экстремумов и т.д.

3. Логарифмическая – , a и b – константы, ln(x) – функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем постепенно стабилизируются.

4. Степенная – , где a и b – константы. Аппроксимация степенной функции используется для экспериментальных данных с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.

5. Экспоненциальная – , где a и b – константы, е – основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Частое ее использование вытекает из теоретических соображений.

Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо щелчком правой кнопки мыши вызвать выплывающее контекстное меню и выбрать пункт Добавить линию тренда. В появившемся диалоговом окне Линия тренда на вкладке Тип выбирается вид аппроксимирующей функции, а на вкладке Параметры задаются дополнительные параметры, влияющие на отображение аппроксимирующей кривой.

Рис. 1.1.

Для рассматриваемого примера по введенным в рабочую таблицу данным необходимо построить диаграмму. Щелчком указателя мыши на кнопке панели инструментов вызвать Мастер диаграмм. В появившемся диалоговом окне выбирать тип диаграммы График. После нажатия кнопки Далее указывать диапазон данных. Проверить положение переключателя Ряды в: столбцах. Выбирать вкладку Ряд и с помощью мыши ввести диапазон подписей оси Х. Нажав кнопку Далее, ввести название диаграммы, название осей X и Y, соответственно. Нажать кнопку Готово. Получен график экспериментальных данных.

Р ис. 1.2.

Осуществить аппроксимацию полученной кривой полиномиальной функцией второго порядка, поскольку кривая довольно гладкая и не сильно отличается от прямой линии. Для этого указатель мыши установить на одну из точек графика и щелкнуть правой кнопкой. В появившемся контекстном меню выбрать пункт Добавить линию тренда. Появится диалоговое окно Линия тренда. Появляется диалоговое окно Линия тренда. В этом окне на вкладке Тип выбрать тип линии тренда – Полиномиальная и установить степень – 2. Затем открыть вкладку Параметры и установить флажки в поля показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). После чего щелкните на кнопке ОК. В результате получите на диаграмме аппроксимирующую кривую. Можно улучшить качество аппроксимации выбором другого типа функции.

Несколько независимых переменных

В тех случаях, когда аппроксимируемая переменная y зависит от нескольких независимых переменных x₁, x₂, …, x_n, y=f(x₁, x₂, …, x_n), подход с построением линии тренда не дает решения. Здесь могут быть использованы следующие специальные функции Excel:

• ЛИНЕЙН и ТЕНДЕНЦИЯ для аппроксимации линейных функций вида:

y=a₀+a₁x₁+a₂x₂+ … +a_nx_n; (1.11)

• ЛГРФПРИБЛ и РОСТ для аппроксимации показательных функций вида:

(1.12)

Функции ЛИНЕЙН и ЛГРФПРИБЛ служат для вычисления неизвестных коэффициентов

a₀, a₁, …, a_n в этих выражениях соответственно, а также коэффициентов детерминации (R²), значений критерия Фишера, стандартных ошибок коэффициентов a_i и ряда других показателей. Обе функции имеют одинаковые параметры:

ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)

ЛГРФПРИБЛ(известные_значения_y;известные_значения_x;конст;статистика)

Здесь:

• известные_значения_y – множество наблюдаемых значений y из выражений (1.11), (1.12);

• известные_значения_x – множество наблюдаемых значений x₁, x₂, …, x_n. Причем, если массив известные_значения_y имеет один столбец, то каждый столбец массива извнстные_значения_x интерпретируется как отдельная переменная, а если массив известные_значения_y имеет одну строку, то тогда каждая строка массива известные_значения_x интерпретируется как отдельная переменная;

• конст – логическое значение, которое указывает, требуется ли, чтобы константа a₀ была равна 0 (для функции ЛИНЕЙН) или 1 (для функции ЛГРФПРИБЛ). При этом, если конст имеет значение ИСТИНА или опущено, то a₀ вычисляется обычным образом, а если конст имеет значение ЛОЖЬ, то a₀ полагается равным 0 или 1;

• статистика – логическое значение, которое указывает, требуется ли вычислять дополнительную статистику по регрессии, если введено значение ИСТИНА, то дополнительные параметры вычисляются, если ЛОЖЬ, то – нет.

Функции ТЕНДЕНЦИЯ и РОСТ позволяют находить точки, лежащие на аппроксимирующих кривых (1.11) и (1.12), соответственно, для значений коэффициентов a₀, a₁, …, a_n, найденных функциями ЛИНЕЙН и ЛГРФПРИБЛ. Обе функции имеют одинаковые аргументы:

ТЕНДЕНЦИЯ(известные_значения_y;известные_значения_x;новые_значения_x;конст);

РОСТ(известные_значения_y;известные_значения_x;новые_значения_x;конст).

Здесь:

• известные_значения_y – множество значений y;

• известные_значения_x – множество значений x;

• новые_значения_x – те значения x, для которых необходимо определить соответствующие аппроксимирующие или предсказанные значения y. Новые_значения_x должны содержать столбец (или строку) для каждой независимой переменной, как и известные_значения_x. Если аргумент новые_значения_x опущен, то предполагается, что он совпадает с аргументом известные_значения_x;

• конст – логическое значение, которое указывает, требуется ли, чтобы константа a₀ была равна 0 (для функции ТЕНДЕНЦИЯ) или 1 (для функции РОСТ). При этом, если конст имеет значение ИСТИНА или опущено, то a₀ вычисляется обычным образом, а если конст имеет значение ЛОЖЬ, то a₀ полагается равным 0 или 1.

ПРИМЕР 2.

Застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе. Оценку цены офисного здания в заданном районе застройщик предполагает осуществлять на основе следующих переменных: y – оценочная цена здания под офис, x₁ – общая площадь в квадратных метрах, x₂ – количество офисов, x₃ – количество входов, x₄ – время эксплуатации здания в годах. Предполагается, что существует линейная зависимость между каждой независимой переменной (x₁. x₂. x₃ и x₄) и зависимой переменной (y), т.е. ценой здания под офис в данном районе. Застройщик наугад выбирает 11 зданий из имеющихся 1500 и получает следующие данные:

X1	X2	X3	X4	y
2310	2	2	20	142000
2333	2	2	12	144000
2356	3	1,5	33	151000
2379	3	2	43	150000
2402	2	3	53	139000
2425	4	2	23	169000
2448	2	1,5	99	126000
2471	2	2	34	142900
2494	3	3	23	163000
2517	4	4	55	169000
2540	2	3	22	149000

Здесь «полвхода» (1/2) означает вход только для доставки корреспонденции. Найти параметры аппроксимирующего уравнения.

Создать рабочую таблицу исходных данных примера 2.

x1	x2	x3	x4	y
2310	2	2	20	142000
2333	2	2	12	144000
2356	3	1,5	33	151000
2379	3	2	43	150000
2402	2	3	53	139000
2425	4	2	23	169000
2448	2	1,5	99	126000
2471	2	2	34	142900
2494	3	3	23	163000
2517	4	4	55	169000
2540	2	3	22	149000

Выделить блок ячеек F1:J5 под массив результатов. Поскольку уравнение для вычисления уравнения имеет степенной характер (2), вызвать функцию ЛГРФПРИБЛ (панель инструментов Стандартная, кнопка Вставка функции, рабочее поле Категория тип Статистические, рабочее поле Функция вид ЛГРФПРИБЛ). Заполнить рабочие поля: Изв_знач_y – E2:E12, Изв_знач_x – A2:D12, Стат – 1. Нажать сочетание клавиш CTRL+SHIFT+ENTER. В результате в диапазоне F1:J5 будут получены следующие данные:

0,998307	1,018106	1,085435	1,000174	80387,15
8,22E-05	0,003288	0,002479	3,36E-05	0,075827
0,997224	0,006014	#Н/Д	#Н/Д	#Н/Д
538,8904	6	#Н/Д	#Н/Д	#Н/Д
0,077964	0,000217	#Н/Д	#Н/Д	#Н/Д

Здесь первая строка – значения коэффициентов a₄, a₃, a₂, a₁, a₀, соответственно, вторая строка – стандартные ошибки этих коэффициентов, третья строка – коэффициент детерминации R² и стандартная ошибка y, четвертая строка – значение критерия Фишера и число степеней свободы и нижняя строка – сумма квадратов регрессии и остаточная сумма квадратов. Таким образом, искомое аппроксимирующее уравнение имеет вид:

.

Причем точность аппроксимации очень высокая – R²=0,997224.

ПРИМЕР 3.

В условиях примера 2 с помощью функции ТЕНДЕНЦИЯ определить оценочную стоимость здания под офис в том же районе, которое имеет площадь 2500 квадратных метров, три офиса, два входа, зданию 25 лет.

Выделите ячейку Е15 под расчетное (предсказанное) значение y. Поскольку уравнение близко к линейному, вызвать функцию ТЕНДЕНЦИЯ (панель инструментов Стандартная, кнопка Вставка функции, рабочее поле Категория тип Статистические, рабочее поле Функция вид ТЕНДЕНЦИЯ). Заполнить рабочие поля: Изв_знач_y – Е1:Е12, Изв_знач_x – A1:D12, Нов_знач_x – A15:D15. Нажать ОК. В результате в ячейке Е15 получите предсказанное значение y.

	A	B	C	D	E
15	2500	3	2	25	158261,1