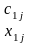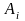Практическое занятие 8 Транспортная задача линейного программирования

Общая постановка транспортной задачи. Требуется организовать доставку однородного груза из m пунктов отправле­ния в n пунктов назначения . При планировании перевозок выдвигают условие: или обеспечить минимальную стои­мость перевозок, или доставить груз за минимальное время.

Пусть – тарифы перевозки (стоимость перевозки) груза из i-го пункта отправления в j-ый пункт назначения; – запасы груза в i-ом пункте отправления; – потребность в грузе в пункте назначения ; 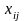– количество груза, перевозимого из i-го пункта отправления в j-ый пункт назначения. Нужно создать такой план перевозок , при котором затраты на его доставку будут минимальными (или обеспечить минимальное время доставки).

Математическая постановка соответствующей ЗЛП имеет вид:

, (1)

; (2)

; (3)

(4)

Всякое неотрицательное решение ЗЛП (48)-(51) называется планом транспортной задачи. План, при котором целевая функция (48) принимает минимальное значение, называется оптимальным планом транспортной задачи .

Обычно данные для транспортной задачи записывается в виде таблицы (табл.15):

Таблица 15

Пункт отправления	Запасы продукции	Пункт назначения
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…
Потребности			…		…

Общее количество груза y поставщиков единиц, общая потребность в грузе в пунктах назначения единиц. Если выполняется равенство

= , (5)

т.е. сумма всех заявок равна сумме всех запасов, то модель транспортной задачи называется закрытой. В противном случае она называется открытой. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие (5): запасы груза в пунктах отправления и потребности в пунктах назначения должны совпадать. Открытую модель можно преобразовать в закрытую. Пусть

> . Введем фиктивный (n+1)-й пункт назначения с потребностью b_n+1 = – и со стоимостью перевозок, равной нулю: . Модель стала закрытой. Пусть < . Введем фиктивный (m+1)-й пункт отправления с запасом груза – 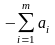и зададим: . Модель снова стала закрытой.

Число неизвестных в транспортной задаче с m пунктами назначения и n пунктами отправления равно 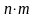, число уравнений в системах (2) и (3) равно n+m.

Выполнение условия (5) означает, что опор­ный план транспортной задачи может иметь не более m+n–1 неизвестных, не равных нулю. Если в опорном плане число отличных от нуля компонент равно (m+n–1), план называют невырожденным. В противном случае – вырожденным планом.

Для построения опорного плана существует несколько методов. Наиболее часто используются метод северо-западного угла и метод минимального элемента.

Метод северо-западного угла. При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. В каждой клетке таблицы исходных данных приводится соответствующее значение . В каждую клетку таблицы нужно занести значение . Заполнение клеток таблицы условий начинается с клетки для неизвестного х₁₁ , расположенной вверху слева («северо-западный угол») и заканчивается клеткой для неизвестного . В столбце «запасы» указываются запасы для каждого пункта отправления, а в строке «потребности» – потребности каждого пункта назначения.

Пример 1. Найти план перевозок данной транспортной задачи (табл.16) методом северо-западного угла. Используем обозначения – клетка таблицы, соответствующая значениям . В клетках табл.16 в верхнем правом углу даются значения . Таблица 16 дает информацию о наличии и требованиях товара до начала перевозок.

Таблица 16

	60	70	120	130	100
140	2	3	4	2	4
180	3	4	1	4	1
160	9	7	3	7	2

Решение. Модель задачи закрытая, так как

и .

Начинаем заполнение таблицы с клетки (1, 1). Так как 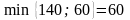, то назначаем величину . Нужды первого потребителя полностью удовлетворены, а в клетках (2, 1), (3, 1) ставим прочерк (табл.32). У первого поставщика в запасе осталось 140–60=80 единиц груза.

В клетку (1, 2) внесем значение . В клетках (2, 2) и (2, 3) ставим прочерк. Второй потребитель полностью обеспечен. У первого поставщика осталось теперь 80–70=10 единиц груза.

Заполним клетку (1, 3): . Запасы первого поставщика израсходованы, в клетках (1, 4) и (1, 5) табл.17 ставим прочерк.

Таблица 17

	60	70	120	130	100
140	2 60	3 70	4 10	2 –	4 –
180	3 –	4 –	1 110	4 70	1 –
160	9 –	7 –	3 –	7 60	2 100

Переходим к клетке (2, 3), далее аналогично заполняем оставшиеся клетки. Суммарные расходы на перевозку груза составляют (денежных единиц) при опорном плане

.

Метод минимальной стоимости. Суть метода минимальной стоимости заключается в выборе клетки таблицы с минимальным тарифом. Выбор пунктов назначения и отправления целесообразно производить, ориентируясь на тарифы перевозок. На каждом шаге выбирается клетка таблицы с минимальным тарифом.

Пример 2. Найти план перевозок заданной транспортной задачи (табл.31) методом минимальной стоимости.

Решение задачи дано в табл.33. Начать можно с любой из клеток (2, 3), (2, 5), так как . Заполнение табл.33 начинаем с клетки (2, 3): . Нужды третьего потребителя удовлетворены, в клетках (1, 3), (3, 3) ставим прочерки.

Вновь выбираем для оставшихся клеток. Процесс продолжаем, пока не заполним все клетки. В результате получим опорный план

.

Таблица 18

	60	70	120	130	100
140	2 60	3 –	4 –	2 80	4 –
180	3 –	4 –	1 120	4 –	1 60
160	9 –	7 70	3 –	7 50	2 40

Суммарные расходы на перевозку грузов составят:

(ден.ед.).

Пример 3 Зам директора по персоналу фирмы по установке кондиционеров должен составить 3 пары команд из техника – установщика и специалиста по маркетингу для работы по установке кондиционеров индивидуальным клиентам. Пары составляются из новых сотрудников, среди которых произведен психологический тест на взаимную совместимость . Индекс совместимости изменяется от 20 баллов ( враждебность) до 1 балла (возможность дружеских отношений) . Данные приведены в таблице (табл 19):

Таблица 19

Маркетолог Техник	Николай	Петр	Алексей
Евгений	18	9	6
Максим	8	13	4
Тимур	19	7	12

Составьте математическую модель задачи, позволяющую найти наиболее оптимальное распределение по парам, которое обращает в минимум индекс совместимости.

Решение. Такие задачи называют задачами о назначениях.

Каждый сотрудник должен быть назначен только один раз т.е имеем 9 переменных Переменные в итоге должны принять какое-либо из двух возможных значений : 0 или 1. Например, если то значит будет создана команда из техника Евгения и специалиста по маркетингу Алексея. Если то такая команда создаваться не будет. Очевидно, суммы переменных по строкам и столбцам должны быть равны единице, т.к. каждый из техников и специалистов по маркетингу может быть включен только в одну команду. Запретов на составление определенных пар нет . Целевую функцию – суммарный индекс совместимости команд следует устремить к минимуму. Итак, получим математическую модель задачи:

Оптимальное решение задачи может быть найдено теми же методами, что и решение транспортных задач.