1. Выбор метода оценки косвенно измеряемой величины

   1. Проверка значимости остаточного члена разложения в ряд Тейлора

Остаточным членом можно пренебречь, если

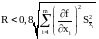, (2.33)

где 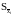– среднеквадратическое отклонение среднего арифметического аргумента x_i.

Отклонения в (2.2) при этом должны быть взяты из полученных значений погрешностей такими, чтобы они максимизировали выражение для остаточного члена R.

2. Проверка гипотезы отсутствия корреляционной связи между погрешностями результатов измерений аргументов

Для всех пар аргументов вычисляется оценка коэффициента корреляции между погрешностями аргументов:

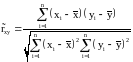, (2.34)

где x, y – пара аргументов;

n – минимальное число измерений среди x и y.

При условии, что распределение случайных погрешностей результатов измерений аргументов не противоречит нормальному распределению, критерием отсутствия корреляционной связи между погрешностями результатов измерений аргументов является выполнение неравенства:

, (2.35)

где t_p – коэффициент Стьюдента, соответствующий доверительной вероятности p и числу степеней свободы (n – 2).

Если хотя бы для одной пары аргументов условие (2.6) не выполняется, гипотеза отвергается.

3. Выбор метода

Метод линеаризации (п. 2.1.2) допустим, если оба условия (2.4) и (2.6) выполняется. В противном случае необходимо применять метод приведения (п. 2.1.3).

2. Метод линеаризации

   1. Нахождение результата измерения

Результат измерения вычисляется по формуле:

. (2.36)

2. Вычисление среднеквадратическое отклонение среднего арифметического

Среднеквадратическое отклонение среднего арифметического косвенного измерения находится по формуле:

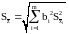, (2.37)

где b_i – весовой коэффициент аргумента x_i:

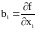. (2.38)

3. Доверительные границы случайной погрешности

Доверительные границы случайной погрешности результата косвенного измерения при условии, что распределения погрешностей результатов измерений аргументов не противоречат нормальным распределениям, вычисляются по формуле (1.19), где число степеней свободы определяется выражением:

. (2.39)

4. Границы неисключенной систематической погрешности

Если неисключенные систематические погрешности результатов измерений аргументов заданы границами _i, то доверительные границы неисключенной систематической погрешности результата косвенного измерения вычисляются по формуле:

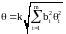, (2.40)

где k – коэффициент, равный 1,1 при доверительной вероятности P = 0,95 и 1,4 при P = 0,99. Если же число суммируемых погрешностей m  4, то коэффициент k определяется по графику (рис. 1.1).

Если неисключенные систематические погрешности результатов измерений аргументов заданы доверительными границами _i, соответствующими вероятностям P_i, то доверительные границы неисключенной систематической погрешности результата косвенного измерения вычисляются по формуле:

, (2.41)

где k_i – коэффициент, равный 1,1 при доверительной вероятности P = 0,95 и 1,4 при P = 0,99. Если же число суммируемых погрешностей m  4, то коэффициент k_i определяется по графику (рис. 1.1).

5. Граница погрешности результата измерения

Если выполняется условие

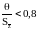, (2.42)

то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата

. (2.43)

Если

, (2.44)

то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата

. (2.45)

Если оба условия (2.13) и (2.15) не выполняются, то доверительную границу погрешности результата косвенного измерения вычисляют по формуле:

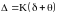, (2.46)

где K – коэффициент, зависящий от доверительной вероятности и от отношения 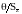(табл. 2.1).

Таблица 2.4

Значения коэффициента K в зависимости от отношения и вероятности P

P
	0,5	0,75	1	2	3	4	5	6	7	8
0,95	0,81	0,77	0,74	0,71	0,73	0,76	0,78	0,79	0,80	0,81
0,99	0,87	0,85	0,82	0,80	0,81	0,82	0,83	0,83	0,84	0,85