3. Равномерный (прямоугольный) закон распределения и его числовые характеристики.

Определение. Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности φ(х) постоянна на этом отрезке и равна нулю вне его, т.е.

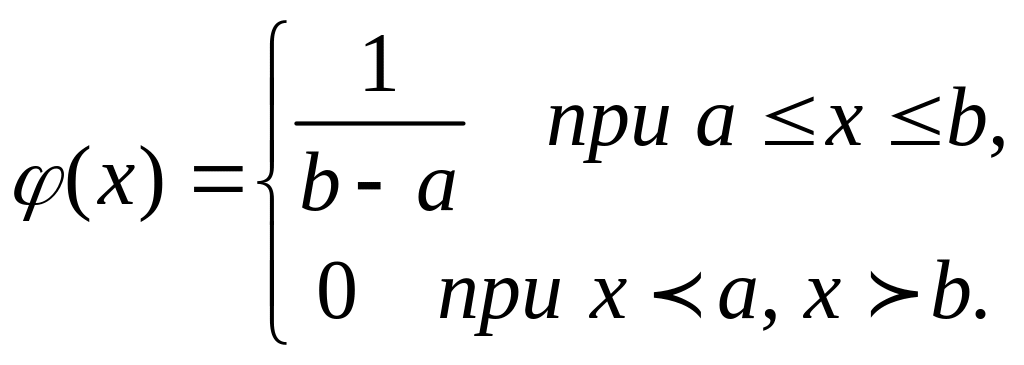
Теорема. Функция распределения случайной величины Х, распределенной по равномерному закону, есть

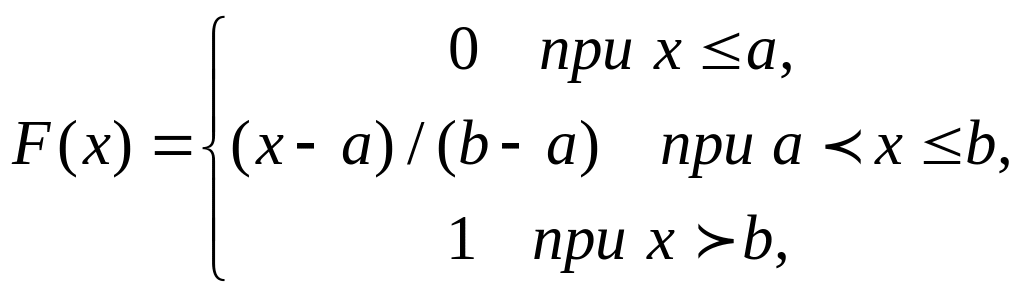
Ее математическое ожидание

,

а дисперсия

.

Доказательство. При х ≤ а функция распределения F(x) = 0.

При а < x ≤ b имеем:

.

При x > b очевидно, что

Математическое ожидание случайной величины Х с учетом его механической интерпетации как центра массы равно абсциссе середины отрезка, т.е. M(X) = .

Дисперсию посчитаем по формуле:

=

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению.

Лекция 6 Тема 5: Непрерывные случайные величины. Нормальный закон распределения

ПЛАН

1. Определение нормального закона распределения.

2. Формулы для определения вероятностей: а) попадания нормально распределенной случайной величины в заданный интервал; б) ее отклонения от математического ожидания. Правило трех сигм.

3. Центральная предельная теорема. Понятие о теореме Ляпунова.

1. Нормальный закон распределения

Для непрерывных случайных величин особо важное значение имеет нормальный закон распределения. Необходимо знать теоретико-вероятностный смысл его параметров, выражение функции распределения F_N(x) через функцию Лапласа Ф(х), свойства нормально распределенной случайной величины, правило трех сигм, важно четко представлять, что нормальный закон, в отличие от других, является предельным законом, к которому при некоторых весьма часто встречающихся условиях приводит совокупное действие (сумма) п независимых случайных величин Х₁, Х₂, … , Х_n при п.

Определение 1. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами a и ², если ее плотность вероятности имеет вид:

.

Многие величины подчиняются нормальному закону, например, рост человека, дальность полета снаряда и т.п.

Кривую нормального закона распределения называют нормальной кривой или гауссовой кривой.

Теорема 1. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона , т.е. M(X)=a , а ее дисперсия равна параметру ² , т.е. D(X)= ².

Доказательство. Математическое ожидание случайной величины Х:

.

Первый интеграл равен нулю как интеграл от нечетной функции по симметричному промежутку. Второй интеграл – это интеграл Пуассона, равный .

Дисперсия случайной величины Х:

.

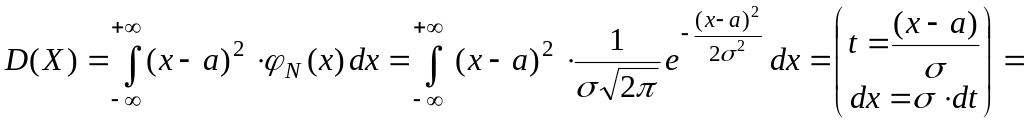
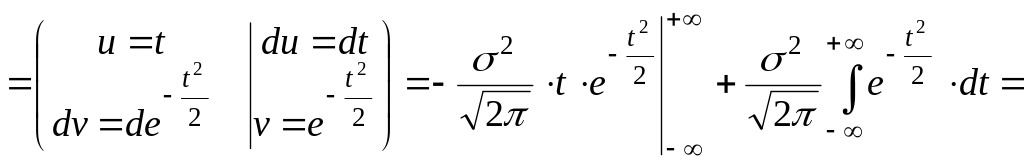
При изменении параметра a гауссова кривая параллельно смещается вдоль оси Ох.

При изменении параметра ² изменяется ордината максимума гауссовой кривой.

Нормальный закон распределения случайной величины с параметрами a=0 и ²=1 называется стандартным (или нормированным), а соответствующая нормальная кривая – стандартной.

Функция распределения НСВ выражается через плотность вероятности по формуле .

Следовательно, функция распределения нормально распределенной случайной величины выражается по формуле 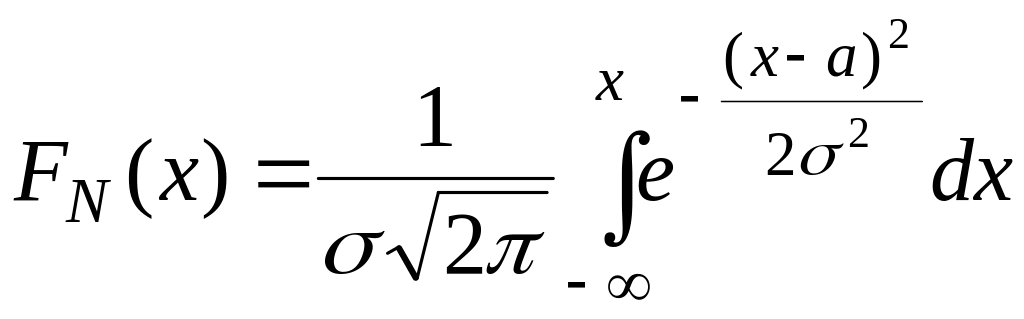, в которой подынтегральная функция не имеет первообразной функции, выражающейся через элементарные функции.

Поэтому ее выражают через функцию Лапласа 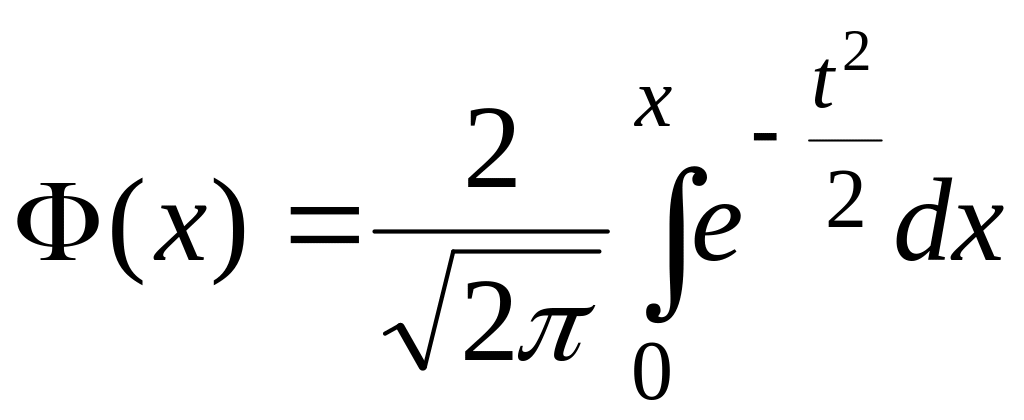, для которой составлены таблицы.

Теорема 1. Функция распределения случайной величины, распределенной по нормальному закону, выражается через функцию Лапласа (x) по формуле:

.

Доказательство.

,

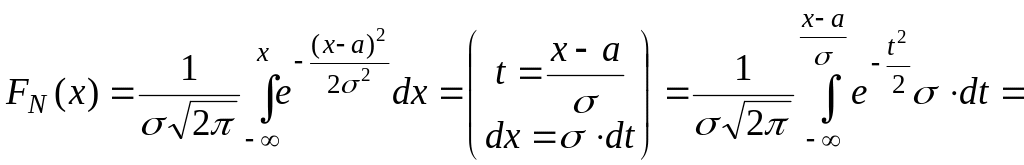
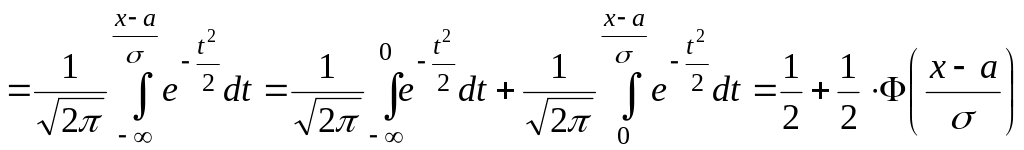так как .