
- •Лекция 8.
- •§ 43. Векторное произведение
- •§ 44. Смешанное произведение трех векторов
- •§ 45. Координаты вектора векторного произведения
- •§ 46. Свойства векторного произведения
- •§ 47. Двойное векторное произведение
- •§ 48. Площадь параллелограмма и треугольника в пространстве.
- •§ 50. Уравнение прямой, проходящей через данную точку в данном направлении
- •§ 51. Общее уравнение прямой
- •§ 52. Направляющий вектор прямой, заданной общим уравнением.
- •§ 53. Частные случаи расположения прямой относительно системы координат
- •§ 54. Параметрические уравнения прямой
- •§ 55. Уравнение прямой, проходящей через 2 точки
- •§ 56. Уравнение прямой в отрезках
- •§ 57. Угловой коэффициент прямой
- •§ 58. Уравнение прямой с угловым коэффициентом
§ 52. Направляющий вектор прямой, заданной общим уравнением.
Из предыдущей теоремы следует, что если прямая задана общим уравнением
относительно
общей декартовой системы координат, то
вектор
![]() и всякий ненулевой вектор, с ним
коллинеарный, является направляющим
вектором этой прямой.
и всякий ненулевой вектор, с ним
коллинеарный, является направляющим
вектором этой прямой.
Теорема 4. Необходимым и достаточным условием того, что вектор коллинеарен прямой, заданной относительно общей декартовой системы координат уравнением
является условие
![]() (1)
(1)
Доказательство.
Отложим вектор
,
от любой точки
данной прямой. Конец р
отложенного вектора будет иметь
координаты
![]() .
.
Вектор коллинеарен данной прямой тогда и только тогда, когда точка р лежит на данной прямой, т.е. тогда и только тогда, когда выполнено равенство
![]()
или
(
,
т.к. точка
![]() лежит на данной прямой). Ч.т.д.
лежит на данной прямой). Ч.т.д.
Теорема 5. Если прямая задана общим уравнением
относительно декартовой прямоугольной системы координат, то вектор
![]()
перпендикулярен этой прямой.
Доказательство. В самом деле, направляющий вектор прямой является вектор , тогда, взяв скалярное произведение, имеем:
![]() ,
,
значит,
вектор
![]() перпендикулярен направляющему вектору
данной прямой, а потому вектор
перпендикулярен и самой прямой. Ч.т.д.
перпендикулярен направляющему вектору
данной прямой, а потому вектор
перпендикулярен и самой прямой. Ч.т.д.
Для общей декартовой системы координат это положение, вообще говоря, не имеет места. Вектор , координаты которого служат коэффициентами в общем уравнении прямой относительно общей декартовой системы координат, называется главным вектором этой прямой.
Главный вектор , заданной уравнением относительно общей декартовой системы координат, неколлинеарен этой прямой. В самом деле, по условию коллинеарности вектора и прямой , имеем:
![]() ,
,
![]() .
.
§ 53. Частные случаи расположения прямой относительно системы координат
Прямая коллинеарна оси Ох, тогда и только тогда, когда А = 0, т.к. направляющий вектор прямой коллинеарен оси Ох тогда и только тогда, когда вторая координата этого вектора равна нулю.
Уравнение
прямой
в случае, если эта прямая коллинеарна
оси Ох,
имеет, таким образом, вид
![]() ,
или
,
или
![]() (где
(где
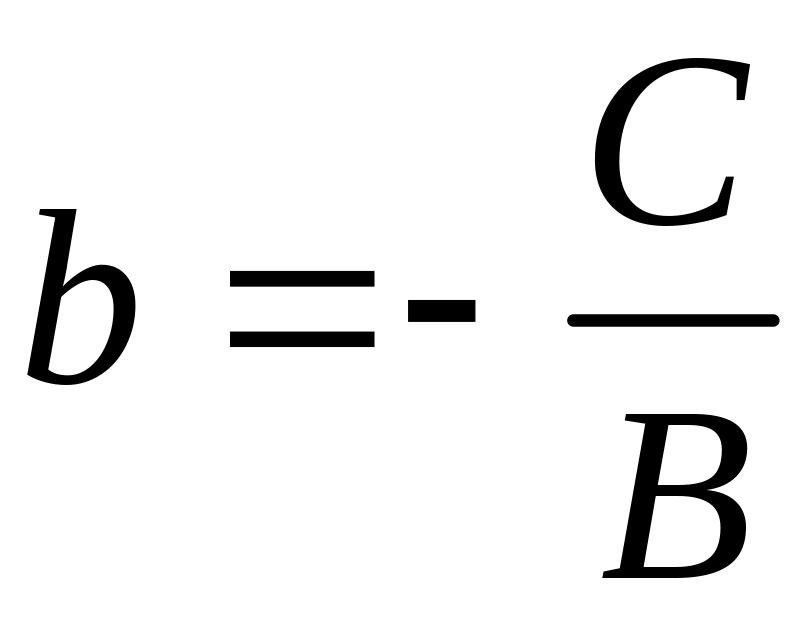 ).
).
Аналогично
доказывается, что прямая
коллинеарна оси Оу
тогда и только тогда, когда В
= 0, т.е. тогда, когда общее уравнение
прямой имеет вид
![]() ,
или
,
или
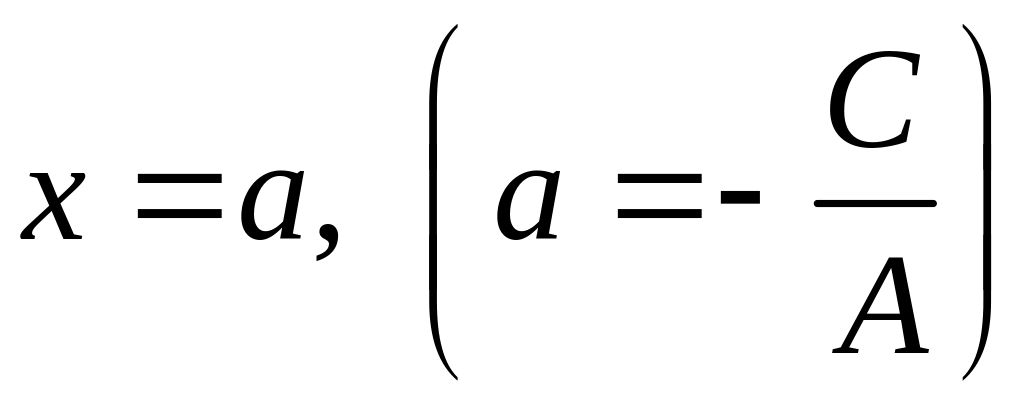 .
.
Необходимым и достаточным условием того, что прямая проходит через начало координат, является равенство С = 0, т.к. в случае С = 0 и только в этом случае уравнение удовлетворяется координатами начала координат.
Таким
образом, общее уравнение прямой,
проходящей через начало координат,
имеет вид
![]() ,
и обратно (т.е. любое однородное уравнение
первой степени определяет прямую,
проходящую через начало координат).
,
и обратно (т.е. любое однородное уравнение
первой степени определяет прямую,
проходящую через начало координат).
§ 54. Параметрические уравнения прямой
Теорема 6. Параметрические уравнения прямой, проходящей через точку и имеющей направляющий вектор , в общей декартовой системе координат имеют вид
![]() .
.
Доказательство.
Пусть
![]() произвольная точка плоскости. Тогда
будет лежать на данной прямой тогда и
только тогда, когда векторы
и
коллинеарны, т.е. тогда и только тогда,
когда они отличаются числовым множителем:
произвольная точка плоскости. Тогда
будет лежать на данной прямой тогда и
только тогда, когда векторы
и
коллинеарны, т.е. тогда и только тогда,
когда они отличаются числовым множителем:
![]() ,
(1)
,
(1)
или в координатах
![]()
откуда
![]()
Если t принимает все действительные значения, то точка М с этими координатами описывает всю данную прямую. Ч.т.д.
Замечание 1. Из соотношения (1) находим
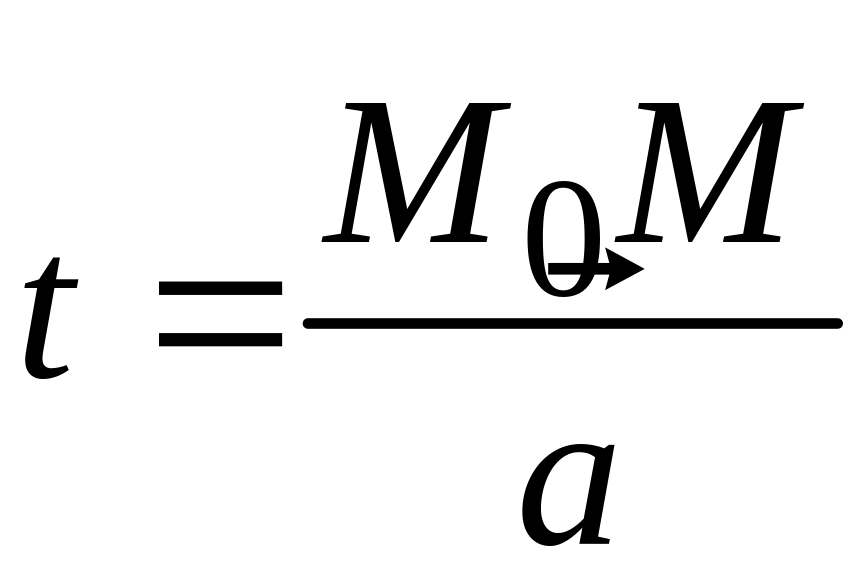 ,
,
т.е. t есть координата точки М на данной прямой в следующей системе координат: - начало координат, - масштабный вектор.
 Замечание
2.
Вводя радиусы векторы
Замечание
2.
Вводя радиусы векторы
![]() и
и
![]() точек
и М,
можно соотношение
,
переписать так:
точек
и М,
можно соотношение
,
переписать так:
![]() ,
,
откуда
![]()
Это
уравнение называется параметрическим
уравнением прямой в векторной форме,
проходящей через точку
![]() и имеющей направляющий вектор
.
и имеющей направляющий вектор
.
