Лабораторная работа №6. «Числовые характеристики двумерных случайных величин».

Теоретическая часть.

Если (ξ,η) – дискретный случайный вектор с распределением

Η ξ	y1	y2	…	ym
x1	p11	p12	…	p1m
x2	p21	p22	…	p2m
…	…	…	…	…
xn	pn1	pn2	…	pnm

то математическое ожидание компонент вычисляют по формулам:

,

Если р_ξ,η(х,у) – совместная плотность распределения двумерной случайной величины (ξ,η), то

,

Дисперсия вычисляется по формулам:

,

Условные математические ожидания вычисляются по формулам:

,

Если р_ξ,η(х,у) – совместная плотность распределения двумерной случайной величины (ξ,η), то

,

Условное математическое ожидание случайной величины ξ является функцией η, то есть М(ξ/η=у)=f₁(y). Функцию f₁(y) называют регрессией случайной величины ξ на случайную величину η. Аналогичные рассуждения можно провести для М(η/ξ=х)=f₂(x).

В случае дискретных величин корреляционный момент вычисляется по формуле:

Если р_ξ,η(х,у) – совместная плотность распределения непрерывной двумерной случайной величины (ξ,η), то

Теоретические вопросы.

1. Как определяются условные математические ожидания компонент системы случайных величин.

1. Что называется коэффициентом корреляции, что он характеризует.

2. Что называется уравнениями регрессии. Что характеризует взаимное расположение линий регрессии.

Практическая часть.

Задание №1. Вычислите математическое ожидание, дисперсию, условные математические ожидания, постройте графики регрессий компонент двумерной случайной величины из задания №1, №2 лабораторной работы №5, определите коэффициент корреляции.

Часть третья «Математическая статистика» Лабораторная работа №7. «Моделирование одномерных случайных величин. Экспериментальный анализ одномерной случайной величины».

Теоретическая часть.

Случайные величины могут подчиняться различным законам распределения. Наиболее часто приходится иметь дело с равномерно распределенными на единичном отрезке случайными последовательностями, которые потом легко преобразовать в любые другие с заданными законами распределения.

Нормально распределенные на интервале (0,1) случайные величины обычно получают из равномерно распределенных по алгоритму:

, где , - псевдослучайное число с равномерным распределением на отрезке (0,1).

Чтобы получить случайную величину равномерно распределенную на интервале (a,b), из случайной величины равномерно распределенной на интервале (0,1), используется преобразование:

Аналогично, с.в. с нормальным законом распределения и произвольными находится из соотношения:

Для преобразования законов могут использоваться методы: обратных функций, Неймана, моделирования условий предельных теорем. Наиболее часто используется метод обратных функций, который основан на известном математическом соотношении, связывающем случайные числа с заданным законом распределения и равномерно распределенными числами на интервале (0,1).

Итак, для получения случайных чисел ξ_i с некоторым требуемым законом распределения F(ξ) из случайных чисел с известным законом распределения необходимо решить уравнение относительно ξ:

Таблица функций для наиболее часто встречающихся распределений:

Распределение, которое нужно получить	или
Экспоненциальное
Гамма распределение (целочисленные η)
Хи-квадрат
Вейбулла
Пуассона	ξ =k, где k – такое наименьшее число, что
Биномиальное	, где ,
Логарифмически нормальное

Группировка данных в вариационный ряд и представление его в виде функции распределения.

1. В исходной таблице найти наибольшее и наименьшее значения.

1. Выяснить диапазон изменения случайной величины .

2. Наметить число интервалов группировки. Для этого можно воспользоваться формулами: , , , S-число групп, n-объем выборки.

3. Определить длину интервала

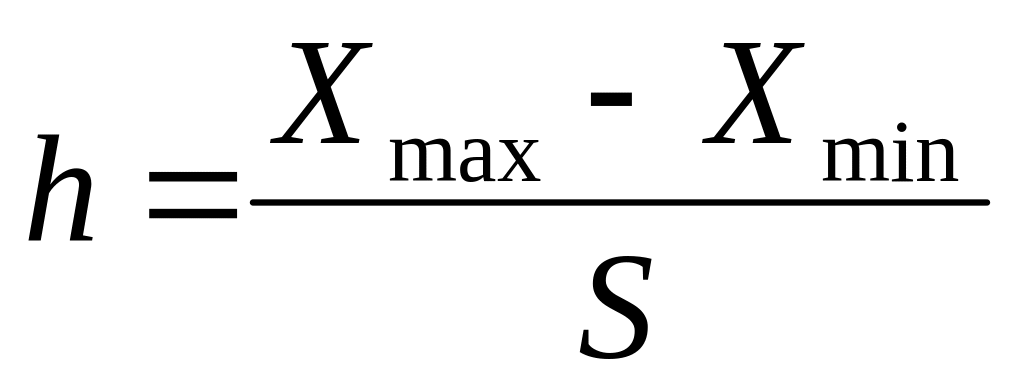
4. Составить интервальный ряд частот и относительных частот.

5. Перейти от интервального ряда к дискретному. Для этого каждый интервал заменить его средним значением.

6. Записать эмпирическую функцию распределения , где n_x – число вариант, меньших чем x.

Графическое изображение вариационного ряда и эмпирической функции распределения.

Графически интервальный вариационный ряд изображается либо в виде гистограммы относительных частот, либо в виде гистограммы частот.

Дискретный ряд изображается в виде полигона частот или относительных частот.

Вычисление числовых характеристик.

Среднее арифметическое - .

Исправленная дисперсия - .

Исправленное среднеквадратическое отклонение - .

Момент к-ого порядка - .

Коэффициент асимметрии - .

Эксцесс - .

Коэффициент вариации - .

Пример построения гистограммы нормального распределения в среде MathCad:

Чтобы создать график в виде гистограммы, необходимо войти в диалоговое окно формат выбранного графика, перейти на вкладку трассировки и установить в поле Тип элемент списка гистограмма (solidbar).

Теоретические вопросы.

1. Какая совокупность называется генеральной.

1. Какие способы формирования выборки вы знаете.

2. Какие вариационные ряды вы знаете.

3. Как графически изобразить вариационный ряд.

4. Что определяет эмпирическая функция распределения.

5. Что характеризуют числовые характеристики распределения.

Практическая часть.

Задание №1. С помощью случайного датчика сформировать выборку объема n, подчиненную указанному в условии варианта закону распределения. Сгруппировать данные в вариационный ряд, перейти к дискретному. Построить эмпирическую функцию распределения.

Задание №2. Изобразить графически полученные интервальный и дискретный вариационный ряды.

Задание №3. Вычислить числовые характеристики полученных распределений.

Варианты к лабораторной работе №7:

Вариант №1.

Задание №1. Экспоненциальное. Гамма-распределение.

Вариант №2.

Задание №1. Вейбулла. Пуассона.

Вариант №3.

Задание №1. Биномиальное. Логнормальное.

Вариант №4.

Задание №1. Хи-квадрат. Логнормальное.

Вариант №5.

Задание №1.Пуассона. Хи-квадрат.

Вариант №6.

Задание №1. Вейбулла. Экспоненциальное.

Вариант №7.

Задание №1. Экспоненциальное. Пуассона.

Вариант №8.

Задание №1. Биномиальное. Хи-квадрат.

Вариант №9.

Задание №1. Гамма распределение. Биномиальное.

Вариант №10.

Задание №1. Вейбулла. Хи-квадрат.