Лабораторная работа № 3-о

Определение длины волны с помощью дифракционной решетки

Цель работы. Определение длин волн линий спектра ртутной лампы.

КРАТКАЯ ТЕОРИЯ. Вблизи краев отверстий или экранов фронт волны искажается, вследствие чего изменяется направление волнового вектора. Отклонение световых лучей от прямолинейного пути при прохождении света вблизи краев экрана, отверстий (или других неоднородностей) называется дифракцией. Если дифрагированные волны являются когерентными, то дифракция сопровождается интерференционными явлениями.

Различают два вида дифракции: дифракция Френеля и дифракция Фраунгофера. Если источник света и точка наблюдения находятся от препятствия достаточно далеко, так что можно считать падающие и дифрагированные волны плоскими, то в этом случае имеет место дифракция Фраунгофера. Все остальные случаи дифракции относятся к дифракции Френеля. В данной работе изучается дифракция Фраунгофера на дифракционной решетке.

Дифракция Фраунгофера от щели.

Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели. Пусть плоская монохроматическая волна падает нормально плоскости щели шириной а (Рис.1). Оптическая разность хода между крайними лучами MC и ND, идущими от щели в произвольном направлении , равна:

 = NF = asin.

Разобьем щель MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна /2. Всего на ширине щели уложится (:/2) зон.

Очевидно, что число зон Френеля будет зависеть от угла . Из построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю.

Это позволяет записать условия дифракционного минимума (при четном числе зон) и дифракционного максимума (при нечетном числе зон):

min asin =  2m (m = 1,2,3…..) (1)

max asin =  (2m+1) (2)

 = 0 – центральный дифракционный максимум.

M N

 /2

F



C D

Линза

Экран

-3/a -2/a -/a 0 +/a +2/a +3/a

Рис.1

Дифракционная решетка. Одномерная дифракционная решетка – это система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Если ширина щели – а, а ширина непрозрачных участков – b, то величина d = a + b называется постоянной (периодом) дифракционной решетки.

Дифракционная картина от решетки определяется как результат взаимной интерференции волн, идущих от всех щелей. Так как распределение интенсивности на экране зависит только от направления дифрагированных лучей, то перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Это означает, что при множестве щелей дифракционные картины, создаваемые отдельными щелями, будут одинаковыми.

Рассмотрим дифракционную решетку из двух щелей (Рис.2). Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть главные минимумы интенсивности света будут наблюдаться в направлениях, определяемых условием:

Условие главных минимумов: asin =  m (m = 1,2,3…..) (3)

Вследствие взаимной интерференции лучей от двух щелей в некоторых направлениях возникнут дополнительные минимумы. Эти направления определяются условием равенства разности хода лучей, посылаемых от эквивалентных точек (например, M и С), /2, 3/2, 5/2 и т.д.

M N C D MC = d  F  MN = a NC = b К L Линза Экран 0 Рис.2

Условие дополнительных минимумов: dsin =  (2m+1) (4) (m = 0,1,2,3.) Для вывода условий наблюдения главных максимумов рассмотрим лучи, испускаемые одноименными точками щелей (например, лучи МK и CL). Легко видеть, что эти лучи имеют одинаковую разность хода  = dsin. Очевидно, что любому лучу, испущенному первой щелью, можно сопоставить луч, испущенный второй щелью, причем разность их хода будет равна разности хода лучей МK и CL.

Таким образом, действие второй щели и всех последующих щелей будет усиливать действие первой щели, если

dsin =  2m = m (m = 0,1,2,3…..)

Это условие носит название условие главных максимумов:

dsin = m (m = 0,1,2,3…..) (5)

Положение главных максимумов зависит от длины волны. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (m = 0), будут разлагаться в спектр, фиолетовая часть которого будет находиться ближе к центру дифракционной картины, красная – дальше от центра. Это свойство дифракционной решетки разлагать белый свет в дифракционный спектр обусловило ее широкое применение в спектральных приборах.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения длины волны в спектре излучения источника света с помощью дифракционной решетки на оптической скамье собирается установка, включающая источник света S (ртутная лампа), щель Щ, дифракционную решетку Р и линейку Л (рис.3).

Р +2 lm +1 Щ S  -1 L -2 Рис. 3

Щель освещается источником света. Миллиметровая линейка Л укрепляется перпендикулярно к оси оптической скамьи. Штрихи линейки располагаются параллельно штрихам дифракционной решетки. Щель рассматривается через решетку глазом.

На линейку проецируется изображение главных максимумов, положение которых отмечается в таблицах 1, 2 или 3, соответственно, для фиолетовых, зеленых или желтых линий. Угол дифракции определяется из отношения расстояния l_m между максимумом нулевого порядка и центром линии m-го порядка к расстоянию L между щелью и решеткой. После определения синуса угла дифракции из соотношения sin = рассчитывают длину волны соответствующей линии исходя из условия наблюдения главных максимумов (5):

dsin = m (m = 0,1,2,3…..)

ЗАДАНИЕ.

1. Ознакомиться с приборами, применяемыми в данной работе. Определить величину периода дифракционной решетки d, которая указана на ее оправе. Собрать на оптической скамье установку, установив дифракционную решетку на заданном преподавателем расстоянии L от щели; включить ртутную лампу.

2. Измерить не менее 3-х раз положение левого и правого максимумов относительно центрального максимума для фиолетовой линии спектра. Результаты измерений занести в Таблицу 1.

d = …… мм; L = ….... мм Таблица 1

Цвет линии: ФИОЛЕТОВЫЙ
m	lm,лев	lт,прав	 lт 	sinm	ф,i	i
1
2
3
Средн.	ХХХХ	ХХХХ	ХХХХ	ХХХХ

3. Повторить измерения положений левого и правого максимумов для зеленой и желтой линий. Результаты измерений занести, соответственно, в Таблицы 2 и 3.

d = …… мм; L = ……. мм Таблица 2

Цвет линии: ЗЕЛЕНЫЙ
m	lm,лев	lт,прав	 lт 	sinm	з,i	i
1
2
3
Средн.	ХХХХ	ХХХХ	ХХХХ	ХХХХ

d = …… мм; L = ……. мм Таблица 3

Цвет линии: ЖЕЛТЫЙ
m	lm,лев	lт,прав	 lт 	sinm	ж,i	i
1
2
3
Средн.	ХХХХ	ХХХХ	ХХХХ	ХХХХ

4. Рассчитать соответствующие углы дифракции и длины волн фиолетовой, зеленой и желтой линий спектра ртутной лампы.

5. Оценить погрешности измерений .

6. Результаты измерений представить в виде:

Фиолетовая линия	Зеленая линия	Желтая линия
 = (  ) нм  = ….. %	 = (  ) нм  = ….. %	 = (  ) нм  = ….. %

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Уравнение и графическое изображение световой волны. Световой вектор.

2. Энергия, переносимая световой волной. Вектор Пойнтинга. Интенсивность света.

3. В чем заключается явление дифракции света? Когда оно наблюдается? Виды дифракции.

4. Принцип Гюйгенса-Френеля и объяснение на его основе явления дифракции.

5. В чем заключается метод зон Френеля, его применение.

6. В чем заключается различие между дифракцией на одной щели, на двух щелях и на дифракционной решетке.

7. Объяснить наличие главных максимумов, дополнительных минимумов при дифракции света на дифракционной решетке.

8. Показать, как выводится условие наблюдения главных максимумов дифракционной решетки.

9. Почему дифракционная решетка разлагает белый свет в спектр? Применение дифракционных решеток.

10.Как изменится дифракционная картина, если закрыть половину щелей решетки? 1/4? Провести наблюдение.

11.Как изменится дифракционная картина, если на решетку направить волны под большим углом падения? Провести наблюдение.

ЛИТЕРАТУРА.

1. Трофимова Т.И. Курс физики. М.: Высш.шк., 1985., Гл. 23, §§ 177-181.

2. Савельев И.В. Курс общей физики. Кн.2. Электричество и магнетизм. Волны. Оптика. М.:”Наука”, 1998, Гл.XVIII, §§ 125-130.

3. Практикум по общей физике. Под ред. проф. В.Ф.Ноздрева. М., «Просвещение», 1971, Гл.IV, С.250.

ЛАБОРАТОРНАЯ РАБОТА № 4-о

ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ЛИНЗ

ЦЕЛЬ РАБОТЫ: Определение фокусного расстояния собирающей линзы.

КРАТКАЯ ТЕОРИЯ. Геометрическая оптика базируется на законе прямолинейного распространения света в однородных средах и на законах отражения и преломления света. Также используется понятие светового луча. Световой луч – геометрическая линия, вдоль которой распространяется энергия электромагнитных волн.

Преломление на сферической границе. На рис. 1 показан ход параксиальных лучей от точечного источника S₁ через сферическую границу раздела двух сред с показателями преломления n₁ и n₂; i₁ — угол падения, r₁ — угол преломления. В точке S₂ получается изображение.

П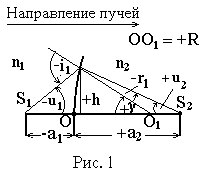 ринято следующее правило знаков: расстояния отсчитываются от вершины О сферической поверхности; отрезки, которые откладываются против хода лучей, записываются со знаком минус, по ходу луча — со знаком плюс; отрезки, которые откладываются по перпендикуляру к оптической оси вверх, записываются со знаком плюс, вниз — со знаком минус; углы отсчитываются от оптической оси S₁S₂, углы падения и преломления — от нормали; если отсчёт идёт по часовой стрелке, то угол записывается со знаком плюс, против часовой стрелки — со знаком минус.

Из чертежа видно, что: , = r₁+u₂, , , На основании закона преломления для параксиальных лучей:

n₁i₁=n₂r₁, n₁(u₁)=n₂(u₂) или

(1)

Tочки S₁ и S₂, являющиеся центрами гомоцентрических пучков, которые преобразуются этой системой, называются сопряжёнными точками. Соотношение (1) называется уравнением сопряжённых точек.

Величина называется оптической силой сферической поверхности.

О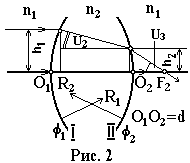 птическая сила линзы. Линзой называется тело из прозрачного материала, которое ограничено двумя сферическими поверхностями. Такие линзы имеют ось симметрии, которая называется главной оптической осью. Линзу будем рассматривать как идеальную оптическую систему. Идеальная оптическая система даёт изображение точечного источника в виде точки. Достаточно хорошим приближением идеальной оптической системы может быть центрированная система, если на неё падают параксиальные пучки. В дальнейшем рассматриваются только идеальные оптические системы.

Построим ход луча, который направлен параллельно главной оптической оси О₁О₁ (рис.2). Среда по обе стороны линзы одинакова (показатель преломления n₁). Толщина линзы d, показатель преломления стекла линзы n₂. Точка F₂, в которой лучи, падающие параллельно главной оптической оси, пересекают оптическую ось, называется фокусом. Применим уравнение (1) к сферическим поверхностям I, II, а затем к линзе в целом. Обозначим оптические силы соответственно

n₁u₁+n₂u₂=₁h_1, (2)

n₂u₂+n₁u₃=₂h_2, (3)

n₁u₁+n₁u₃=h_1. (4)

Учитывая, что:

получим:

(6)

Для тонкой линзы (d << R), поэтому

 = ₁ + ₂. (7)

Кардинальные точки и плоскости оптической системы. Направим луч 1 параллельно оптической оси (рис. 3). Продолжим его до пересечения с продолжением луча, проходящего через фокус F₂, получим точку К₂. Навстречу лучу 1 направим луч 2. Получим точку К₁. Проведём через эти точки плоскости перпендикулярно главной оптической оси.

Т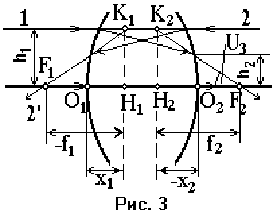 акие плоскости называются главными плоскостями, а точки H₁ и H₂ — главными точками. Главные плоскости являются геометрическим местом сопряжённых точек, которые расположены на одинаковых расстояниях от оптической оси и находятся по одну сторону от неё. Эта пара плоскостей и точек относится к основным (кардинальным) элементам любой идеальной оптической системы.

Расположение главных точек относительно оптических центров сферических поверхностей линзы определяется отрезками x₁ и x₂.

Из рис.3 следует: . Учитывая (2), (4), (5), получим:

Второй парой кардинальных элементов являются фокусы F₁ и F₂ и фокальные плоскости, которые проходят через фокусы перпендикулярно оптической оси. Фокус F₂, расположенный в пространстве изображений, называется задним фокусом, фокус F₁, расположенный в пространстве предметов, называется передним фокусом. Фокус является сопряжённой точкой для бесконечно удалённой точки. Расстояние от главной точки до фокуса называется фокусным расстоянием ( f ).

Фокусное расстояние связано простым соотношением с оптической силой. Из рис. 3 следует:

h₁/f₂=u₃ (10)

Учитывая (4) (при условии u₁=0) , получим:

f₂ = n₁ , ₍₁₁₎

f₁ = n₁. (12)

Если фокусное расстояние выражается в метрах, то оптическая сила выражается в диоптриях. Оптическая система имеет положительную оптическую силу, если передний фокус её F₁ лежит левее точки Н₁, а задний фокус F₂ — правее точки Н₂ (предполагается, что свет распространяется слева направо).

Третьей парой кардинальных элементов являются узловые точки, которые обладают тем свойством, что луч (или его продолжение), входящий в линзу через одну узловую точку, при выходе из неё пройдёт через другую узловую точку под таким же углом (по значению и знаку) к главной оптической оси. Плоскости, проходящие через узловые точки перпендикулярно главной оптической оси, называются узловыми.

Если среда по обе стороны линзы одинакова, узловые и главные плоскости совпадают.

У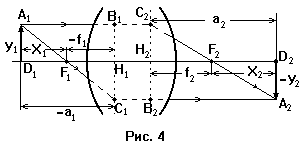 равнение линзы. Построим изображение в линзе (рис. 4). Расположение фокусов и главных точек указано на чертеже. Отсчёт расстояний производится от соответствующих главных плоскостей с учётом правила знаков.

Из подобия треугольников А₂В₂С₂ и F₂Н₂С₂ следует:

; (13)

из подобия треугольников А₁В₁С₁ и F₁Н₁С₁:

. (14)

Из (13) и (14) следует:

. (15)

Это уравнение сопряжённых точек линзы. Если среда по обе стороны линзы одинакова, то f₁ = f₂ = f. Тогда уравнение (15) можно записать в виде:

или . (16)

Для тонкой линзы обе главные плоскости совпадают и проходят через её оптический центр; поэтому a₁, a₂, f₁, f₂ отсчитываются от оптического центра линзы.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА И ИЗМЕРЕНИЯ

Для определения фокусных расстояний используется оптическая скамья, на которой с помощью рейтеров устанавливаются освещённое матовое стекло с прямоугольной сеткой, белый экран и соответствующие линзы.

Определение фокусных расстояний тонких положительных линз.

1-й способ. Перемещением линзы и экрана добиваются получения чёткого изображения сетки на экране. Измеряется по делениям линейки оптической скамьи расстояние а₁ между линзой и сеткой и расстояние а₂ между линзой и экраном.

П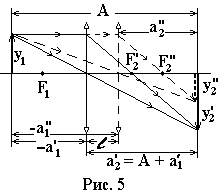 еред измерениями необходимо проверить совпадение указателей на рейтерах с плоскостями, в которых находятся сетка, экран и плоскость тонкой линзы, проходящая через оптический центр. При отсутствии совпадения необходимо вводить поправку при измерениях. Фокусное расстояние рассчитывается по формуле (16) с учётом правила знаков.

Измерения проводятся для 5-10 различных значений а₁ и а₂; одна половина измерений проводится при увеличенном изображении сетки, другая — при уменьшенном изображении сетки. Данные заносятся в таблицу 1.

Таблица 1.

№ п/п	а1, …	1/а1	а2, …	1/а2
1
2
…
…
10

Для проверки формулы (16) строится график, на котором по оси Ох откладываются значения 1/а₁, а по оси Оу - значения 1/а₂; все точки должны располагаться на одной прямой, которая отсекает на осях Oх и Oу отрезки, равные 1/f. Определить среднее значение f.

Оценить погрешность измерений. Следует обратить внимание на то, что фокусное расстояние тонкой линзы имеет смысл определять с точностью до толщины линзы.

2-й способ. Линза, экран и сетка размещаются так же, как и при измерениях первым способом. Измеряется только одно расстояние а₁ (или a₂); измеряются линейные размеры сетки y₁ и линейные размеры её изображения y₂; находится линейное увеличение y₂/y₁; это отношение равно a₂/a₁. Из равенства y₂/y₁= a₂/а₁ находят второе расстояние а₂ (или а₁). Для расчёта f применяется формула (16).

Измерения проводятся для 3 различных значений увеличения (при увеличении больше единицы). Результаты заносят в таблицу 2.

Таблица 2.

№ п/п	а1	у1	у2	у2/у1	а2 = а1	f
1
2
3
Средн.	ххххх	ххххх	ххххх	ххххх	ххххххххх

3-й способ. Если расстояние A между сеткой и экраном будет больше 4f, то посредством перемещения линзы можно получить два изображения предмета  увеличенное и уменьшенное  при неизменном расстоянии A (см. рис.5).

В этом случае уравнение (16) можно представить в следующем виде:

Два корня этого уравнения и соответствуют двум возможным положениям линзы относительно сетки. На рис. 5 указаны два положения линзы и соответствующие построения изображений; большему значению a₁ (по модулю) соответствуют штриховые линии.

Если обозначить разность  = l, то получится расчётная формула:

.

В этом способе измеряется расстояние между сеткой и экраном А и расстояние l между 2-мя положениями линзы, соответствующими увеличенному и уменьшенному изображениям.

Таблица 3.

№ п/п	А	 	 	l	f
1
2
3
Средн.	ххххх	ххххх	ххххх	ххххх

Окончательные результаты представить в виде сравнительной таблицы.

Таблица 4.

1-й способ	2-й способ	3-й способ
f = (f  f) cм  = ….. %	f = (f  f) cм  = ….. %	f = (f  f) cм  = ….. %