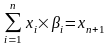- •Стратегии инвестирования на финансовых рынках Семенихин а.И.
- •Введение и обзор
- •Модель Марковица a. Характеристики инвестиционного портфеля и основные допущения модели
- •B. Анализ функции полезности инвесторов
- •С. Результаты комбинирования ценных бумаг Ожидаемая доходность комбинации двух и более ценных бумаг
- •Риск инвестиционного портфеля
- •D. Графическое определение взаимосвязи риска и доходности для инвестиционного портфеля, состоящего из ценных бумаг двух видов
- •E. Соединение графиков доходности и риска для инвестиционного портфеля с двумя видами ценных бумаг
- •F. Эффективные инвестиционные портфели
- •Одноиндексная модель у. Шарпа
- •Модель Тобина
- •Модель capm, рыночная модель
- •Инвестиционный проект как опцион
- •Альтернативные концепции. Гипотеза эффективного рынка
- •Приложение к модели г. Марковица a. Вывод функции полезности и формулы риска для портфеля
- •2. Вывод формулы риска инвестиционного портфеля для ценных бумаг двух типов
- •3. Алгебраическое решение для риска портфеля, содержащего ценные бумаги двух видов
- •B. Элементы теории вероятности
Одноиндексная модель у. Шарпа
Модель Г. Марковица требует определения математического ожидания и дисперсии доходности каждой ценной бумаги, а также ковариации между доходами отдельных ценных бумаг. Последняя операция является особенно трудоемкой. Так, например, для анализа 100 акций необходимо рассчитать около 500 ковариаций.
У. Шарпу удалось упростить модель Г. Марковица, предложив, так называемую, индексную модель. Мы рассмотрим простой вариант – одноиндексную модель У. Шарпа.
В основе одноиндексной модели лежит линейная регрессионная модель, которая связывает доходность какой-либо ценной бумаги с тем или иным рыночным параметром (валовым внутренним продуктом, уровнем инфляции, индексом потребительских цен и т.п.). Шарп У. связывал доходность одной ценной бумаги рыночного портфеля с доходностью всего портфеля, в качестве которого принимал пакет акций, входящих в биржевой индекс S&P500.16
Уравнение
линейной регрессии строится следующим
образом. На основании исторических
данных определяются параметры
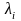 и
и
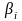 уравнения:
уравнения:
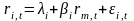 ,
где
,
где
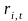 -
доходность
-й
ценной бумаги в момент
-
доходность
-й
ценной бумаги в момент
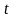 ;
;
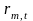 -
доходность рыночного портфеля в момент
;
-
доходность рыночного портфеля в момент
;
- свободный член уравнения, так называемый коэффициент «альфа»;
- коэффициент «бета»
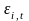 -
случайная ошибка (предполагается, что
математическое ожидание случайной
ошибки равно 0).
-
случайная ошибка (предполагается, что
математическое ожидание случайной
ошибки равно 0).
Неизвестные параметры и регрессионной модели определяются методом наименьших квадратов из условия минимизации суммы квадратов случайной ошибки:
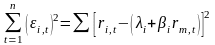
Необходимо взять производные данного выражения по и , и приравнять их нулю.
Минимум случайной ошибки достигается при следующих соотношениях:
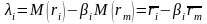 ;
;
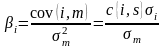
Заметим, что минимум суммы квадратов отклонений достигается тогда, когда отклонения считаются от математического ожидания случайной величины, то есть когда теоретические значения доходности ценной бумаги равные математическому ожиданию доходности.
При минимальной случайной ошибке коэффициент «альфа» равен разнице между среднеарифметической доходностью -й ценной бумаги и среднеарифметической доходностью портфеля, умноженной на коэффициент «бета», а коэффициент «бета» - отношению ковариации -й ценной бумаги с рыночным портфелем к дисперсии портфеля. Напомним, что дисперсия равна ковариации ценной бумаги с самой собой.
Напомним также, что коэффициенты ковариации и корреляции связаны следующими соотношениями:
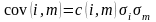
Теперь проведем расчеты необходимых показателей случайных величин (математического ожидания и дисперсии), по имеющимся историческим данным за - моментов времени.
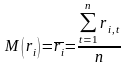
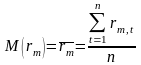
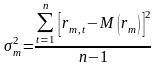


На основе вычисленных показателей случайных величин мы уже можем рассчитать параметры и регрессионного уравнения. Напомним, что:
;
.
Для решения задачи оптимизации портфеля ценных бумаг, подобные расчеты мы должны провести для каждой ценной бумаги из портфеля.
Итак, мы рассчитали параметры регрессионного уравнения, которые дают минимальную величину случайной ошибки. Но нам неизвестна еще эта величина.
Уточним допущения предложенной регрессионной модели:
Математическое ожидание ожидаемой случайной ошибки для всех акций равно 0;
Дисперсия случайных ошибок для всех акций - постоянная величина;
Для каждой акции портфеля отсутствует корреляция между наблюдаемыми на каждом шаге расчета случайными ошибками, то есть
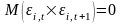 ;
;Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле, то есть
 ;
;Отсутствует корреляция между случайными ошибками регрессионного уравнения и рыночной доходности, то есть
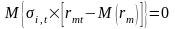 .
.
Теперь мы можем корректно рассчитать дисперсию случайной ошибки для каждой ценной бумаги.
По
определению дисперсии,
 .
Так как
.
Так как
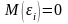 по первому допущению.
по первому допущению.
Поэтому
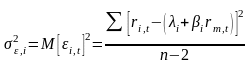
Среднеарифметическое
значение дисперсии случайной ошибки
вычисляется делением на
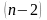 ,
так как две степени свободы были потеряны
при вычислении
и
.
,
так как две степени свободы были потеряны
при вычислении
и
.
Теперь мы можем вычислить среднеарифметическое значение доходности и риск (дисперсию) любой отдельной ценной бумаги портфеля с учетом случайной ошибки. Вернемся к нашей основной регрессионной модели:
, где
- доходность -й ценной бумаги в момент ;
- доходность рыночного портфеля в момент ;
- свободный член уравнения, так называемый коэффициент «альфа»;
- коэффициент «бета»
- случайная ошибка (предполагается, что математическое ожидание случайной ошибки равно 0).
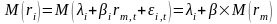 .
.
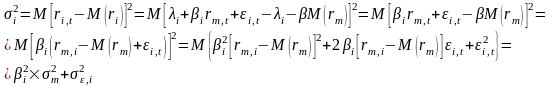
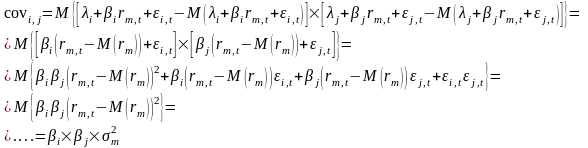
Итак, подведем итоги:
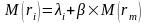

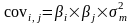
Становится понятным, почему одноиндексная модель оптимизации портфеля ценных бумаг требует меньше расчетов, чем модель Марковица Г. Дело в том, что отпадает необходимость считать парные ковариации по всем ценным бумагам. Одноиндексная модель предполагает, что показатели любой ценной бумаги зависят только от выбранного индекса, его доходности и риска.
Заметим, что риск отдельной ценной бумаги портфеля раскладывается на две составляющих – риск, связанный с колебаниями портфеля в целом, нестабильностью всего рынка, и риск случайной ошибки регрессионного уравнения, то есть неустойчивости самой бумаги:
Разделим
обе части равенства на
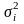 .
Получим:
.
Получим:
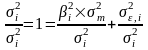
Первое слагаемое показывает, какую долю в суммарном риске ценной бумаги можно описать с помощью регрессионной модели, а какую следует приписать ее неточности.
Мы рассчитали среднеарифметическую доходность и дисперсию каждой ценной бумаги на рынке. Теперь мы можем определить ожидаемую доходность и риск портфеля, состоящего, например, из ценных бумаг.
Математическое ожидание доходности портфеля из ценных бумаг представляется следующим образом:
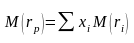 ,
где
,
где
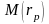 -
математическое ожидание доходности
портфеля из
ценных
бумаг;
-
математическое ожидание доходности
портфеля из
ценных
бумаг;
- доля -й ценной бумаги в портфеле из ценных бумаг;
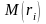 -
математическое ожидание доходности
-й
ценной бумаги.
-
математическое ожидание доходности
-й
ценной бумаги.
Подставим в эту формулу выражение для математического ожидания -й ценной бумаги:
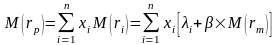
Разделим слагаемые на две части, зависимую и не зависимую от рынка:
 .
.
Для
упрощения записи мы можем представить
рыночный индекс как показатель условной
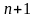 ценной бумаги.
ценной бумаги.
Для этого введем следующее:
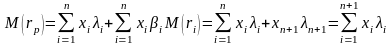 ,
где
,
где
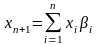 и
и
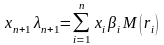
 -
портфельная «бета»
-
портфельная «бета»
Дисперсия портфеля из ценных бумаг:
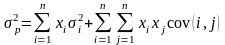
Подставим в формулу выражения, полученные ранее, а именно:
Получим, с учетом условного введения ценной бумаги:
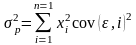 .
.
При этом
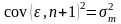 и
и
Сформулируем одноиндексную модель У. Шарпа в целом в сравнении с моделью Г. Марковица.
Модель Г. Марковица:
При условиях:
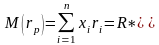
Одноиндексная модель У. Шарпа
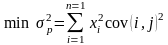 .
.
При условиях: