Контрольные вопросы

1. Что такое силовая линия магнитного поля?

2. В чём выражается принцип суперпозиции для магнитного поля?

3. Сформулируйте закон Био-Савара-Лапласа.

4. В чём выражается правило правого винта?

5. Что является источниками магнитного поля?

6. Какова размерность вектора магнитной индукции в СИ?

7. Используя закон Био-Савара-Лапласа, докажите формулы (11.4). (11.5), (11.6), (11.11).

8. В чем состоит метод определения горизонтальной составляющей индукции магнитного поля Земли? Получите расчётную формулу (11.14).

9. Почему полученное в работе экспериментальное значение горизонтальной составляющей индукции магнитного поля Земли может отличаться от табличного?

Используемая литература

[1] §§ 22.1, 22.2;

[2] §§ 15.2, 15.4, 15.5;

[3] §§ 2.35, 2.37, 2.38, 2.39;

[4] т. 2 §§ 40, 42, 47, 50;

[5] §§ 109, 110, 119.

Лабораторная работа 2-12

Изучение магнитного поля короткой катушки

Цель работы: измерение индукции магнитного поля на оси катушки конечной длины; проверка принципа суперпозиции.

Теоретическое введение

П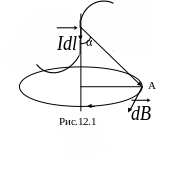 одобно тому, как электрическое поле создается электрическими зарядами, магнитное поле создается электрическими токами. Пусть по тонкому неподвижному проводу течет электрический ток силой I. Рассмотрим малую часть провода, которую будем характеризовать вектором . Этот вектор начинается в произвольной точке провода, его модуль равен длине рассматриваемой части провода, а направление совпадает с направлением тока (рис.12.1).

Элемент тока создает в пространстве магнитное поле, индукция которого в произвольной точке А пространства в вакууме определяется законом Био-Савара-Лапласа:

, (12.1)

где – магнитная постоянная; – радиус-вектор, проведенный от элемента тока до рассматриваемой точки (рис.12.1).

Модуль вектора можно найти по формуле:

(12.2)

где  – угол между векторами и . Формула (12.1) была установлена Лапласом при изучении результатов экспериментальных исследований магнитных полей токов в проводах различной формы, которые были проведены Био и Саваром.

Магнитная индукция, создаваемая всем проводом с током, равна сумме векторов магнитной индукции от каждого малого участка тока. Это утверждение носит название принципа суперпозиции. Согласно этому принципу вектор магнитной индукции поля, созданного всем проводником с током, выражается интегралом:

, (12.3)

где интегрирование производится по всему контуру с током.

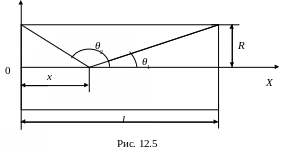
Вычислим индукцию магнитного поля на оси соленоида. Каждый виток соленоида – это круговой ток, поэтому первоначально вычислим индукцию поля на оси кругового витка с током на расстоянии x от центра витка (рис. 12.2).

Элементарная индукция поля, созданного в точке А элементом тока , направлена по правилу буравчика перпендикулярно радиус-вектору , проведенному от элемента тока в точку А (рис.12.2), а ее модуль можно найти из (12.2):

, (12.4)

где α=90⁰ – угол между векторами и . Разложим на две составляющих: – вдоль оси контура (ОХ) и – перпендикулярную оси ОХ, тогда

, . (12.5)

При сложении составляющих магнитного поля , перпендикулярных оси ОА, они компенсируют друг друга вследствие симметрии контура. Поэтому результирующая индукция магнитного поля в точке А направлена вдоль оси кругового тока и равна по модулю:

. (12.6)

Здесь учтено, что величины I, r, β постоянны, а интеграл по контуру равен длине окружности контура. Из рис.12.2 найдем , тогда:

, (12.7)

или:

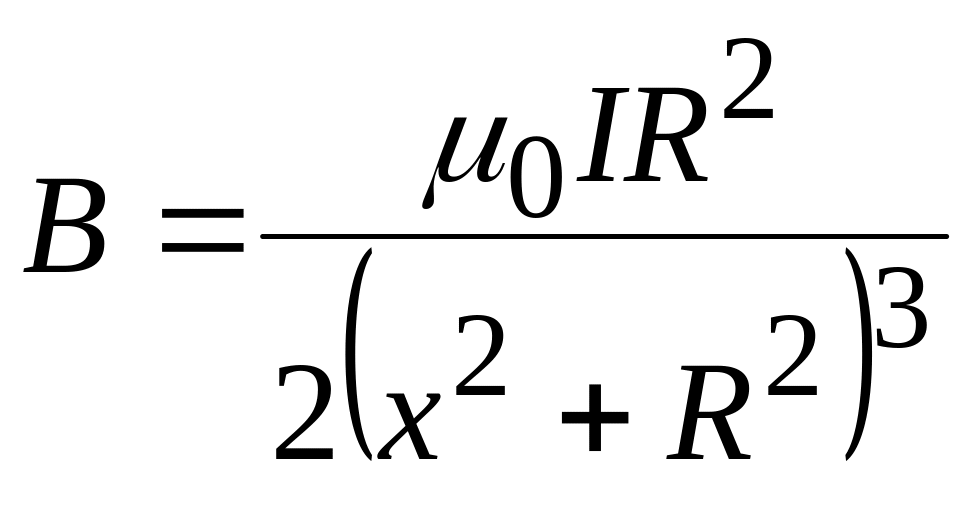. (12.8)

Получим формулу для индукции магнитного поля на оси соленоида длины l и радиуса R, на единицу длины которого приходится витков ( , где N – полное число витков соленоида). На участке длины соленоида будет витков, которые в точке О солено­ида согласно (12.7) создадут индукцию

(12.9)

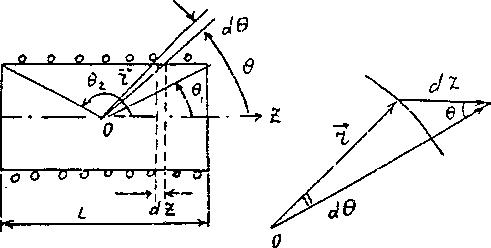
Рис. 12.3 Рис. 12.4

На рис. 12.4 отдельно изображены элемент , радиус-вектор и углы θ и dθ. Из геометрических построений рис. 12.3 и 12.4 следует:

, (12.10)

Подставляем (12.10) в (12.9) и интегрируем в пределах от θ₁ до θ₂:

,

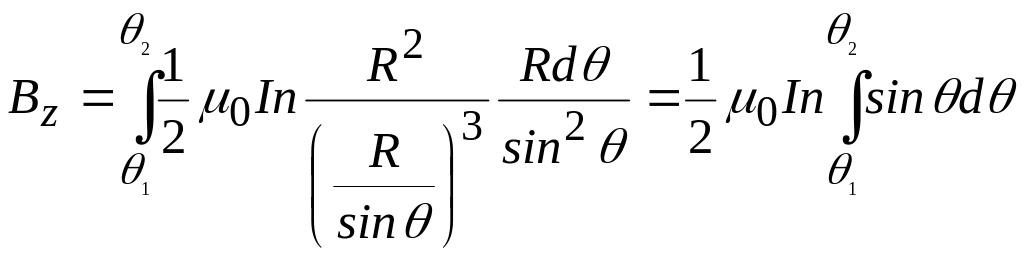. (12.11)

В случае бесконечного соленоида θ₁=0, θ₂=π, и тогда

. (12.12)

Выразим и через x (рис. 12.5) для точек, лежащих на оси соленоида:

, . (12.13)

Подставив (12.13) в (12.11) с учётом того, что , найдём зависимость B(x):

. (12.14)

Эта формула даёт следующие значения магнитной индукции на торцах соленоида и в его середине:

(12.15)

, (12.16)

где D=2R – диаметр соленоида.

Нетрудно убедиться в том, что формула (12.14) справедлива для всех точек на оси соленоида, в том числе при x<0 и x>l . Согласно этой формуле магнитная индукция монотонно убывает до нуля при .

График зависимости B=f(x) изображен на рис. 12.6. При формула (12.16) для магнитной индукции в центре соленоида переходит в полученное ранее выражение (12.12) для бесконечного соленоида.