Почему мы выбрали эту тему:

Изучая геометрию в 7 классе нам больше всего понравилась эта геометрическая фигура, и мы захотели узнать побольше интересного о треугольнике.

Где встречается треугольник в жизни?

Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки. Три точки, образующие треугольник, называются вершинами треугольника, а прямолинейные отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все остальные треугольники невырожденные.

В неевклидовых пространствах в качестве сторон треугольника выступают геодезические линии, которые, как правило, являются криволинейными. Поэтому такие треугольники называют криволинейными.

Элементы треугольника

Треугольник с вершинами A, B и C обозначается как   (см. рис.). Треугольник   имеет три стороны:

• сторона  ;

• сторона  ;

• сторона  .

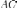Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):

• ;

• ;

• .

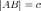Треугольник   имеет следующие углы:

• угол   — угол, образованный сторонами   и   и противолежащий стороне  ;

• угол   — угол, образованный сторонами   и   и противолежащий стороне  ;

• угол   — угол, образованный сторонами   и   и противолежащий стороне  .

Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).

Признаки равенства треугольников

Треугольник на евклидовой плоскости однозначно можно определить по следующим тройкам основных элементов:

• a, b, γ (равенство по двум сторонам и углу лежащему между ними);

• a, β, γ (равенство по стороне и двум прилежащим углам);

• a, b, c (равенство по трём сторонам).

Признаки равенства прямоугольных треугольников:

• по катету и гипотенузе;

• по двум катетам;

• по катету и острому углу;

• по гипотенузе и острому углу.

В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.

Типы треугольников

Типы треугольников
Остроугольный	Тупоугольный	Прямоугольный
Разносторонний	Равнобедренный	Равносторонний

По величине углов

сумма углов треугольника равна 180°.

Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

• Если все углы треугольника острые, то треугольник называется остроугольным;

• Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;

• Если один из углов треугольника 09118000910300прямой (равен 90°), то треугольник называется 0911800103001801809110510300180080прямоугольным. Две стороны, образующие прямой угол, называются 09001051%22катетами"катетами, а сторона, противолежащая прямому углу, называется 00800105010700гипотенузой.

В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.

По числу равных сторон

• Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и 008110501108100биссектриса равнобедренного треугольника, опущенные на основание, совпадают.

• Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

Определения, связанные с треугольником

Все факты, изложенные в этом разделе, из евклидовой геометрии.

Лучи, отрезки и точки

• Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, %22http://ru.wikipedia.org/wiki/%D0%A6%D0%B5%D0%BD%D1%82%D1%80_%D1%82%D1%8F%D0%B6%D0%B5%D1%81%D1%82%D0%B8%22тяжести"центр HYPERLINK "%22центр%20HYPERLINK%20%22http://ru.wikipedia.org/wiki/%D0%A6%D0%B5%D0%BD%D1%82%D1%80_%D1%82%D1%8F%D0%B6%D0%B5%D1%81%D1%82%D0%B8%22тяжести"тяжестинаходится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы. Треугольник с вершинами в серединах называется срединным треугольником.

• Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой %22ортоцентром"ортоцентром треугольника. Треугольник с вершинами в основаниях высот называется ортотреугольником.

• Биссектрисой треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с %22центром%20вписанной%20окружности"центром вписанной окружности (инцентром).

• Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой.

• Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника.

• Серединные перпендикуляры (медиатриссы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.

В равнобедренном треугольнике медиана, высота и биссектриса, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольникразносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.

Чевианы, лежащие на прямых, симметричных медианам относительно биссектрис, называются симедианами. Они проходят через одну точку — %22http://ru.wikipedia.org/wiki/%D0%A2%D0%BE%D1%87%D0%BA%D0%B0_%D0%9B%D0%B5%D0%BC%D1%83%D0%B0%D0%BD%D0%B0%22Лемуана"точку HYPERLINK "%22точку%20HYPERLINK%20%22http://ru.wikipedia.org/wiki/%D0%A2%D0%BE%D1%87%D0%BA%D0%B0_%D0%9B%D0%B5%D0%BC%D1%83%D0%B0%D0%BD%D0%B0%22Лемуана"Лемуана.

Некоторые точки в треугольнике — «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли. Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это — точки Аполлония. Точки   и   такие, что   и   называются точками Брокара.

Прямые

В любом треугольнике центр тяжести, ортоцентр и центр описанной окружности лежат на одной прямой, называемой прямой Эйлера.

Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара. На ней лежат точки Аполлония. Также на одной прямой лежат точки Торричелли и точка Лемуана. Основания внешних биссектрис углов треугольника лежат на одной прямой, называемой осью внешних биссектрис. На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью, она перпендикулярна прямой Эйлера.

Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой %22http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D1%8F%D0%BC%D0%B0%D1%8F_%D0%A1%D0%B8%D0%BC%D1%81%D0%BE%D0%BD%D0%B0%22Симсона"прямой HYPERLINK "%22прямой%20HYPERLINK%20%22http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D1%8F%D0%BC%D0%B0%D1%8F_%D0%A1%D0%B8%D0%BC%D1%81%D0%BE%D0%BD%D0%B0%22Симсона"Симсона данной точки. ПрямыеСимсона диаметрально противоположных точек перпендикулярны.

Треугольники

• Треугольник с вершинами в основаниях чевиан, проведённых через данную точку, называется чевианным треугольником этой точки.

• Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.

• Треугольник ввершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником. Окружностно-чевианный треугольник подобен подерному.

Окружности

• Вписанная окружность — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром.

• Описанная окружность — окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.

• Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их %22радикальный%20центр"радикальный центр — центр вписанной окружности срединного треугольника, называемый точкой Шпикера.

Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера. Центр окружности девяти точек лежит на прямой Эйлера. Окружность девяти точек касается вписанной окружности и трёх вневписанных. Точка касания вписанной окружности и окружности девяти точек называется точкой Фейербаха. Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, ортезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности — окружности Конвея. В любой треугольник можно вписать три окружности таким образом, что каждая из них касается двух сторон треугольника и двух других окружностей. Такие окружности называются окружностями Мальфатти. Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна.

В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром 000010510818гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.

Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна, а отрезки, соединяющие вершины с точками касания вневписанных окружностей — в 020100009000305018точке Нагеля.