2.3.4. Пример решения слау итерационными методами.
Дана система уравнений
Выполним проверку выполнения достаточного условия сходимости.
Проверяем условие диагонального преобладания.
первое уравнение: 4>1+1=2 – выполняется;
второе уравнение: 2<1+5=6 – не выполняется;
третье уравнение: |–1|<1+6=7 – не выполняется.
Таким образом, условие диагонального преобладания для исходной системы уравнений не выполняется и поэтому не может быть гарантирована сходимость итерационных методов к решению. Для данной системы можно добиться выполнения этого условия перестановкой второго и третьего уравнений:
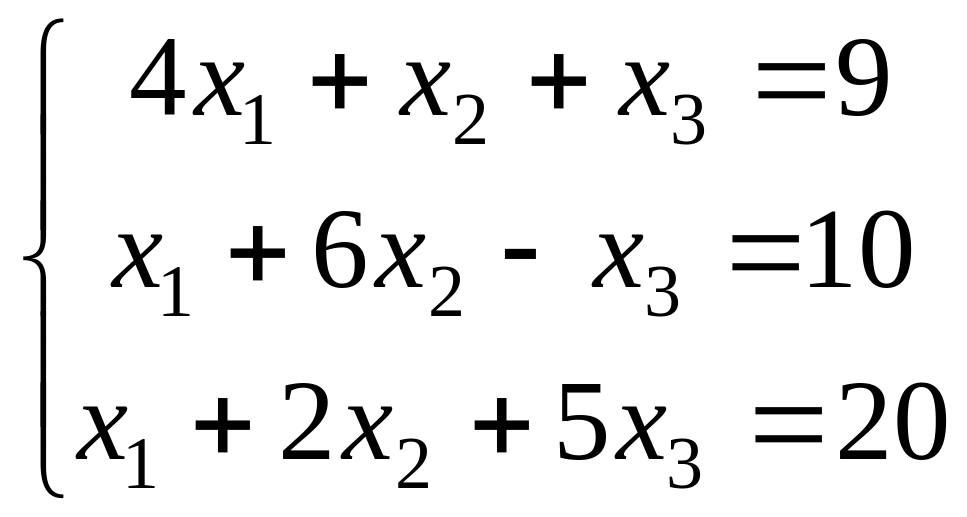
Проверяем условие диагонального преобладания для преобразованной системы:
первое уравнение: 4>1+1=2 – выполняется;
второе уравнение: 6>1+|–1|=2 – выполняется;
третье уравнение: 5>1+2=3 – выполняется.
Решение СЛАУ методом простой итерации.
Схема пересчета в данном случае имеет вид:
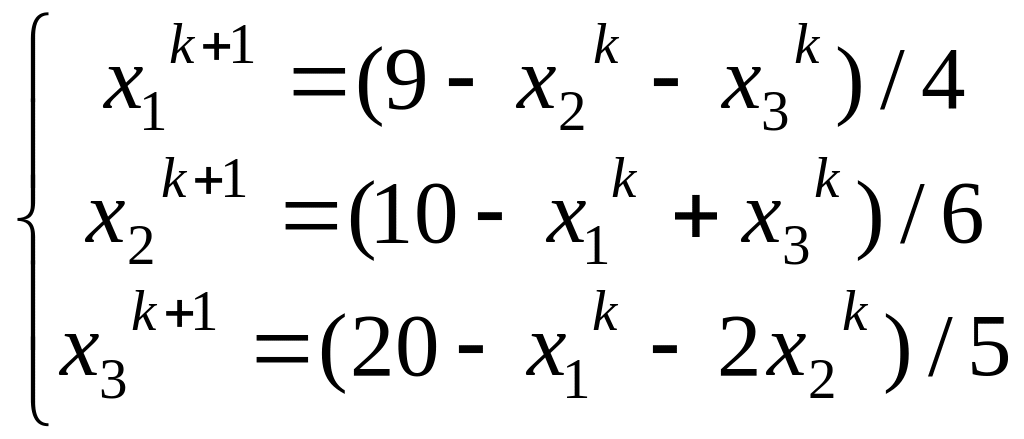
Начальное приближение:
.
Для определения точности приближения воспользуемся нормой вектора
– максимум модуля для элементов вектора.
Первый шаг итерации (
):
.
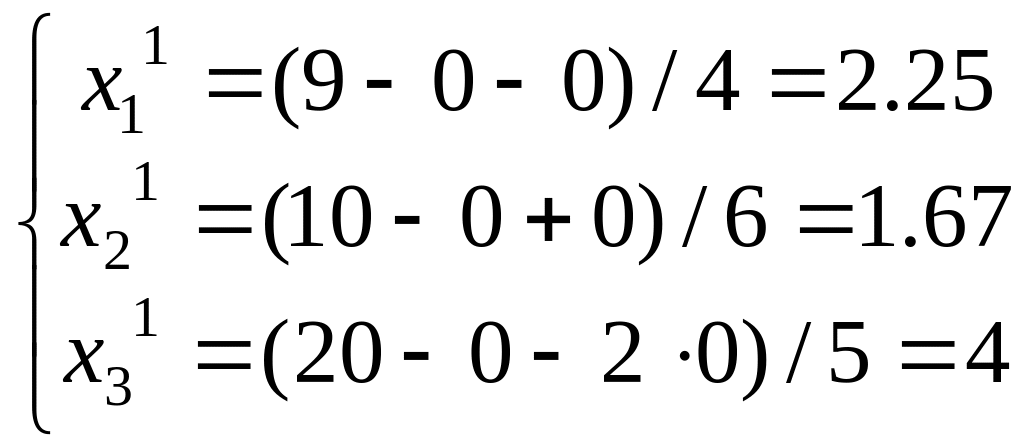
Второй шаг итерации (
):
.
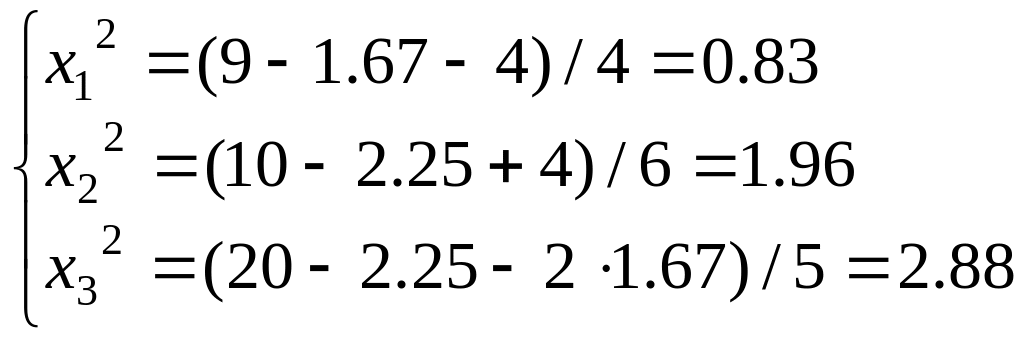
Третий шаг итерации (
):
.
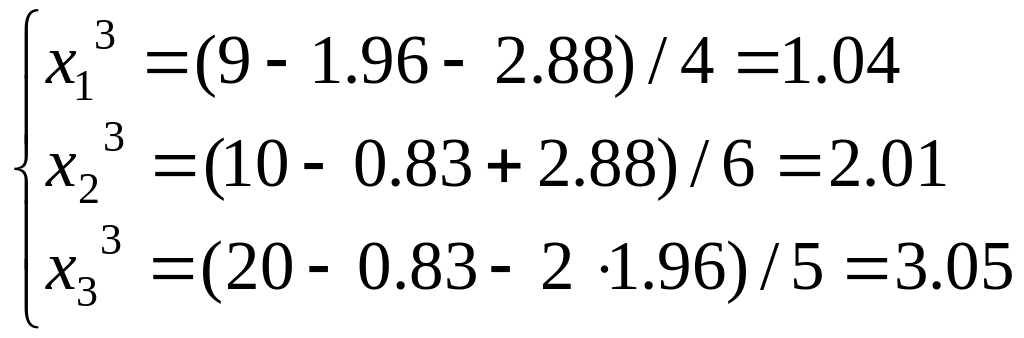
После трех итерационных шагов получаем
приближенное решение СЛАУ:
.
Решение СЛАУ методом Зейделя.
Схема пересчета в данном случае имеет вид:
Начальное приближение: .
Первый шаг итерации ( ):
.
Второй шаг итерации ( ):
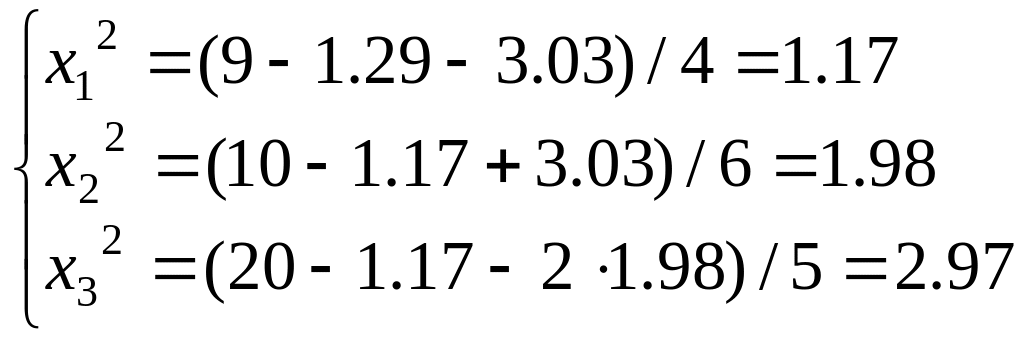
Третий шаг итерации ( ):
.
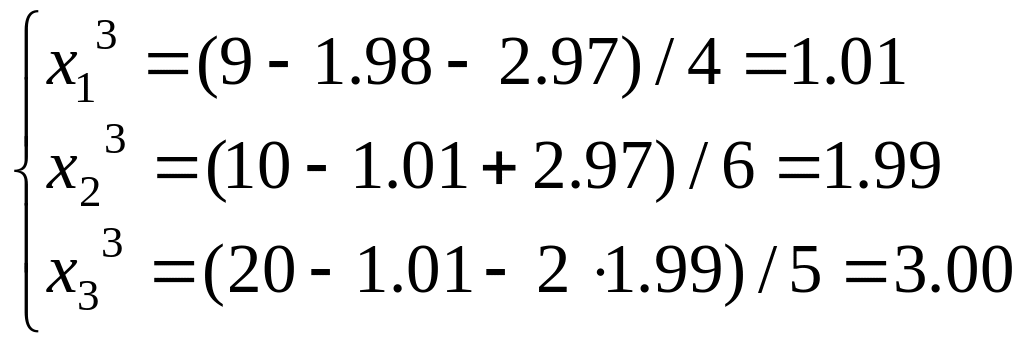
После трех итерационных шагов получаем
приближенное решение СЛАУ:
.
При том, что точное решение данной СЛАУ:
,
– отметим большую точность решения.
полученного методом Зейделя по сравнению
с методом простой итерации за одинаковое
количество итерационных шагов.
2.3.5. Пример программы (лабораторная работа 3).
Варианты задания.
Исходная СЛАУ
,
где
– номер факультета;
– номер группы;
– номер студента по журналу.
Не выполняется условие диагонального преобладания для 1-го и 2-го уранений. Их перестановка позволяет выполнить это условие:
Для определения точности приближения воспользуемся нормой вектора
– норма по модулю.
1. Обычная формулировка
Текст программы на F90
integer,parameter::n=3,kmax=100 real,parameter::s=2,g=3,r=s-g,k=1,r1=s+g+k,a33=2*r1,eps=0.001 real,dimension(n,n)::A=(/4.,1.,s,-1.,5.,g,1.,1.,a33/) real,dimension(n)::b,xk,xk1 b(1)=r+4*k-2;b(2)=r+k+10;b(3)=2*(r*r1+g)+k*s print 100,'matrix A',((a(i,j),j=1,n),i=1,n);print 100,'vector b',b 100 format(/10x,a/(3f10.1)) print 100,'SIMPLE ITERATION'; xk=0; do ki=0,kmax; zk=0; xk1=b; do i=1,n; do j=1,n; if(i/=j) xk1(i)=xk1(i)-a(i,j)*xk(j); enddo; xk1(i)=xk1(i)/a(i,i);zk=zk+abs(xk1(i)-xk(i)); enddo; xk=xk1; if(zk<eps)goto 3 enddo; 3 print '(2x,"ki=",i3,3x,"zk=",f8.6)',ki,zk; print 100,'result',xk print 100,'SEIDEL'; xk=0; do ki=0,kmax; zk=0; do i=1,n; y=b(i) do j=1,n; if(i/=j) y=y-a(i,j)*xk(j); enddo; y=y/a(i,i);zk=zk+abs(y-xk(i)); xk(i)=y enddo; if(zk<eps)goto 4 enddo 4 print '(2x,"ki=",i3,3x,"zk=",f8.6)',ki,zk; print 100,'result',xk
end |
Результаты счета
matrix A
4.0 -1.0 1.0
1.0 5.0 1.0
2.0 3.0 12.0
vector b
1.0 10.0 -4.0
SIMPLE ITERATION
ki= 6 zk=0.000065
result
1.0 2.0 -1.0
SEIDEL
ki= 4 zk=0.000827
result
1.0 2.0 -1.0
Press any key to continue
2. Maтричная формулировка
Текст программы на F90
use dfimsl use linear_operators integer,parameter::n=3,kmax=100 real,parameter::s=2,g=3,r=s-g,k=1,r1=s+g+k,a33=2*r1,eps=0.001 real,dimension(n,n)::A=(/4.,1.,s,-1.,5.,g,1.,1.,a33/),L,U,C1,C2,D real,dimension(n)::b,b1,b2,xk,xk1,di b(1)=r+4*k-2;b(2)=r+k+10;b(3)=2*(r*r1+g)+k*s print 100,'matrix A',((a(i,j),j=1,n),i=1,n);print 100,'vector b',b 100 format(/10x,a/(3f10.1))
D=diag(diagonals(A)); L=0;U=0;do i=1,n-1;do j=i+1,n;U(i,j)=A(i,j);enddo;enddo;L=A-D-U; print 100,'matrix L',((L(i,j),j=1,n),i=1,n); print 100,'matrix D',((d(i,j),j=1,n),i=1,n); print 100,'matrix U',((U(i,j),j=1,n),i=1,n); xk=0 print 100,'SIMPLE ITERATION'; C1=D.ix.(A-D); b1=D.ix.b do ki=0,kmax xk1=b1-matmul(C1,xk) zk=sum(abs(xk1-xk)) xk=xk1;if(zk<eps)goto 1 enddo 1 print '(2x,"ki=",i3,3x,"zk=",f8.6)',ki,zk print 100,'result',xk1 xk=0 print 100,'SEIDEL'; C2=(L+D).ix.U;b2=(L+D).ix.b do ki=0,kmax xk1=b2-matmul(C2,xk) zk=sum(abs(xk1-xk)) xk=xk1;if(zk<eps)goto 2 enddo 2 print '(2x,"ki=",i3,3x,"zk=",f8.6)',ki,zk print 100,'result',xk1
end |
Замечание. Здесь приняты следующие обозначения
,
где
– нижняя треугольная матрица,
– диагональная матрица,
– верхняя треугольная
матрица.
Простая итерация:
,
где
.
Метод Зейделя:
,
где
,
Операторы
use dfimsl
use linear_operators
означают подключение библиотек стандартных подпрограмм dfimsl и linear_operators, соответственно.
В библиотеке linear_operators возможно использовать следующие матричные операции
Математика |
Fortran 90 |
|
A.x.B |
|
.i.A |
|
A.ix.B |
|
A.xi.B |
Результаты счета
matrix A
4.0 -1.0 1.0
1.0 5.0 1.0
2.0 3.0 12.0
vector b
1.0 10.0 -4.0
matrix L
0.0 0.0 0.0
1.0 0.0 0.0
2.0 3.0 0.0
matrix D
4.0 0.0 0.0
0.0 5.0 0.0
0.0 0.0 12.0
matrix U
0.0 -1.0 1.0
0.0 0.0 1.0
0.0 0.0 0.0
SIMPLE ITERATION
ki= 6 zk=0.000065
result
1.0 2.0 -1.0
SEIDEL
ki= 4 zk=0.000827
result
1.0 2.0 -1.0
Press any key to continue