
Контрольная работа
Логические операции
Краткая теория
В алгебре высказываний вводится пять операций над высказываниями: одноместная операция отрицания, и двуместная операция конъюнкция, дизъюнкция, импликация и эквивалентность. Определения этих операций проще всего представить в виде таблицы, где истина представляется значением 1, а ложь значением о.
Таблица логических операций
а |
B |
|
|
|
|
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Иногда
для упрощения записи скобки при
образовании сложных высказываний
опускают при этом порядок логических
операций, определяется так: -,
![]() .
.
Равносильность формул
Две
формулы f(x1,
x2,
…, xn),
g(x1,
x2,
…, xn)
называются равносильными (f(x1,
x2,
…, xn)
![]() g(x1,
x2,
…, xn)),
если для любых конкретных высказываний
x1
= a1,
x2
= a2,
…, xn
= an
их значения совпадают.
Очевидно если формулы f,
g
равносильны, то их таблицы истинности
совпадают. Отсюда доказать равносильность
двух формул можно, построив их таблицы
истинности. Другой способ доказательства
связан с использованием равносильных
преобразований формул, основанных на
лемме о замене: именно, если
g(x1,
x2,
…, xn)),
если для любых конкретных высказываний
x1
= a1,
x2
= a2,
…, xn
= an
их значения совпадают.
Очевидно если формулы f,
g
равносильны, то их таблицы истинности
совпадают. Отсюда доказать равносильность
двух формул можно, построив их таблицы
истинности. Другой способ доказательства
связан с использованием равносильных
преобразований формул, основанных на
лемме о замене: именно, если
![]() и h(x1,
x2,
…, xi,
…, xn)
– произвольная формула, то
и h(x1,
x2,
…, xi,
…, xn)
– произвольная формула, то
h(x1, x2, …, f, …, xn) h(x1, x2, …, g, …, xn)
Конъюнктивная нормальная форма (к.Н.Ф.)
Теорема 1. Любая формула f (x1, …, xn) в алгебре высказываний имеет равносильную ей к.н.ф.
При преобразовании формулы f (x1, …, xn) в к.н.ф. используются в указанной очередности равносильности:

Теорема 2. Формула f является тавтологией тогда и только тогда, когда в её к.н.ф. в каждом дизъюнктивном одночлене какая-то переменная встречается вместе со своим отрицанием
Дизъюнктивная нормальная форма (д.Н.Ф.)
Теорема 3. Любая формула f(x1, …, xn) в алгебре высказываний имеет равносильную ей д.н.ф.
При преобразовании формулы f(x1, …, xn) в д.н.ф. используются в указанной очередности равносильности:
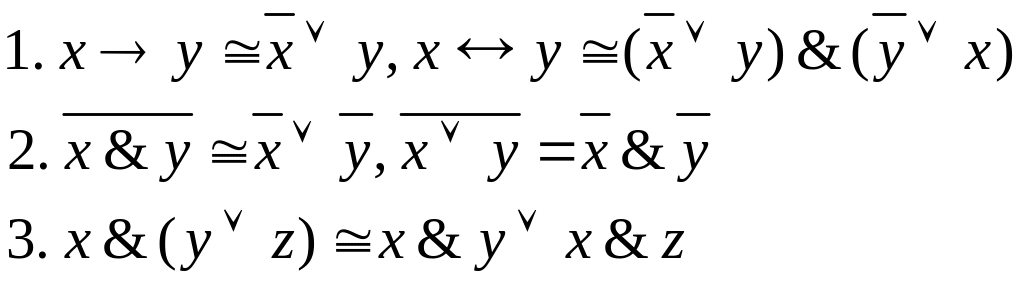
Пример выполнения задания1
Задание 1. Решить систему логических уравнений двумя способами
Вариант 0.
![]()
1-ый способ: Решаем первое уравнение системы. Отыскав все решения первого уравнения, выбираем из них те, которые удовлетворяют второму уравнению.
![]() либо
а = о, либо
либо
а = о, либо
![]() отсюда решениями первого уравнения
будут
отсюда решениями первого уравнения
будут
а = 0, в = 0, с = 0
а = 0, в = 0, с = 1
а = 0, в = 1, с = 0
а = 0, в = 1, с = 1
а = 1, в = 1, с = 1
Подставив найденные решения во второе уравнение, найдем решение системы
0
 0
0 0 = 1 ≠ 0
0 = 1 ≠ 00 0 1 = 0 = 0
0 1 0 = 0 = 0
0 1 1 = 1 ≠ 0
1 1 1 = 1 ≠ 0
Таким образом решениями системы будут 2-е и 3-е решения первого уравнения, т.е.
1) а = 0, б = 0, с = 1
2) а = 0, б = 1, с = 0
2-ой способ. Строим таблицы истинности для левых частей первого и второго уравнений и подчеркиваем строки в которых их значения совпадают с соответствующими значениями первых частей уравнений.
|
|
|
(1) |
|
(2) |
|
а |
б |
с |
в |
а(1) |
а в |
(2) с |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Решения: 1) а = 0, б = 0, с =1.
2) а = 0, в = 1, с = 0
Пример выполнения задания2
Задание 2. Доказать равносильность формул с помощью
а) таблиц истинности,
б) равносильных преобразований.
Вариант 0.
![]()
Решение:
1-ый способ: Строим таблицы истинности для формул f и g.
p |
q |
R |
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
Из построенных таблиц для f и g видно, что их значение для конкретных высказываний совпадают.
2-ой способ: Приведём формулу f равносильными преобразованиями к формуле g.

Преобразование
1 осуществляется с использованием
равносильности
![]() .
Преобразование 2 осуществляется с
использованием дистрибутивности
операции & относительно
.
Преобразование 2 осуществляется с
использованием дистрибутивности
операции & относительно
![]() к двум первым скобкам.
к двум первым скобкам.
Преобразование 3 осуществляется с использованием следующих равносильностей:

Преобразование 4 осуществляется с использованием дистрибутивности операции & относительно . Преобразование 5 осуществляется с использованием равносильностей в), г), использованных при преобразовании 3.
Пример выполнения задания3
Задание 3. Найдите конъюнктивную нормальную форму формулы F. Является ли формула F тавтологией?
Вариант 0.
![]()
Решение:

Последнее
выражение является к.н.ф., так как
представляет собой конъюнкцию
дизъюнктивных одночленов Д1
=
![]() ,
Д2
=
,
Д2
=
![]() ,
Д3
= z,
Д4
=
,
Д3
= z,
Д4
=
![]() .
Очевидно формула f
не является тавтологией, так как условие
теоремы 2 не выполняется.
.
Очевидно формула f
не является тавтологией, так как условие
теоремы 2 не выполняется.
Пример выполнения задания 4
Задание 4. Найти д.н.ф. формулы f. Является ли формула f противоречием.
Вариант 0.
![]()
Решение:

Поскольку полученная формула является дизъюнкцией конъюнктивных одночленов, то это д.н.ф. Согласно теореме 2 она равносильна 0, т.е. является противоречием.
