§2. Некоторые приёмы решения систем нелинейных уравнений

Рассмотрим систему двух уравнений относительно двух неизвестных:

,

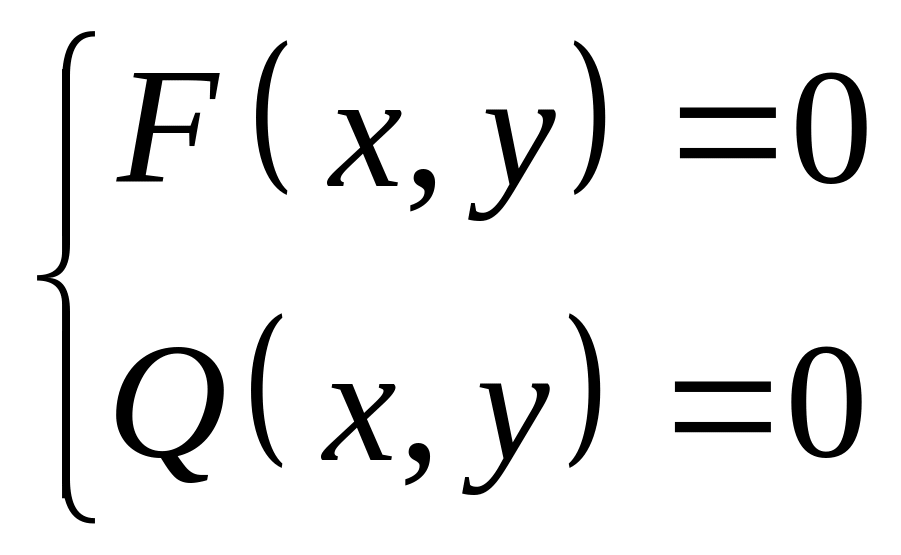(1)

в которой хотя бы одно из выражений или не является линейным по х или по у. Нет универсального способа решения систем вида (1), хотя основным методом аналитического решения остаётся метод исключения одной неизвестной. Перечислим некоторые приёмы решения таких систем, наиболее часто применяемые на практике.

1. Исключение одной неизвестной в простейшем случае, когда в системе есть линейное уравнение

ПРИМЕР

Решим систему .

Решение

;

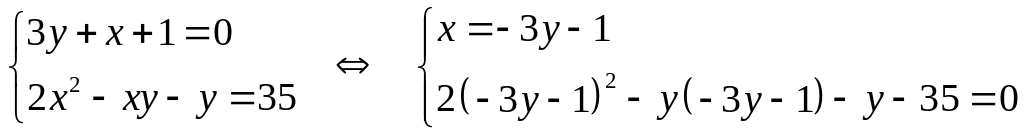решаем второе уравнение относительно у:

;

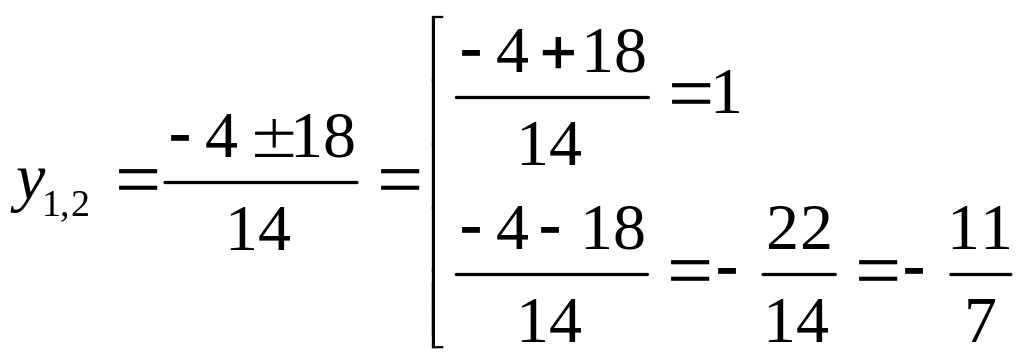продолжаем решать систему с найденными значениями у:

система .

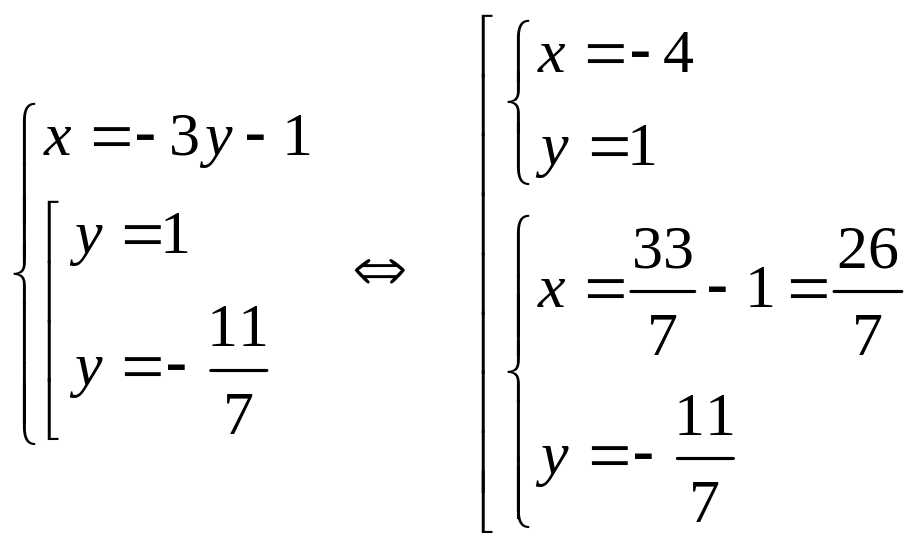Система имеет два решения, которые подтвердим проверкой.

Проверка:

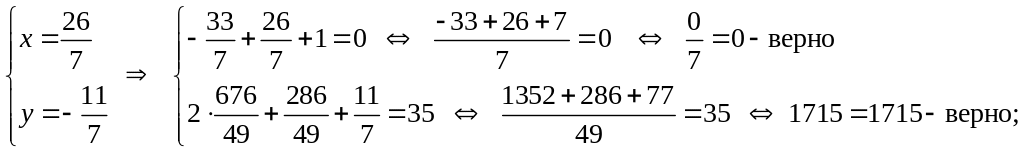
так как каждое из двух найденных решений удовлетворяет всем уравнениям данной системы, то эти решения являются правильными.

Ответ: , .

2. Преобразование системы с целью получить линейное уравнение.

ПРИМЕР

Решим систему .

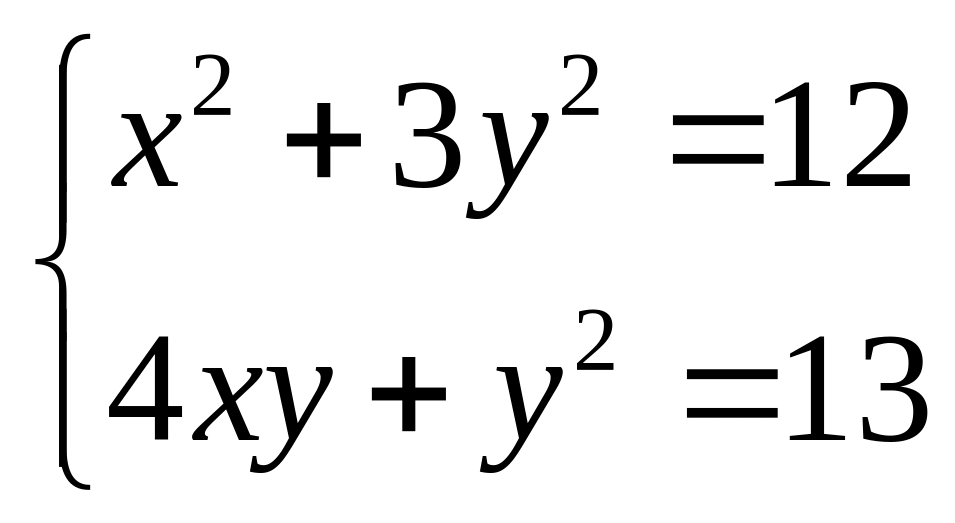Решение

Получим линейное уравнение алгебраическим сложением уравнений данной системы:

Теперь заменяем в исходной системе одно из уравнений на совокупность полученных двух линейных уравнений и далее заменяем систему на совокупность двух систем, в каждой из которых исключаем одну неизвестную способом подстановки:

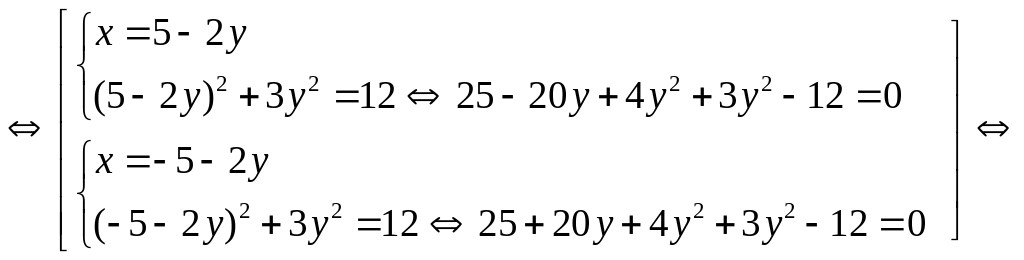
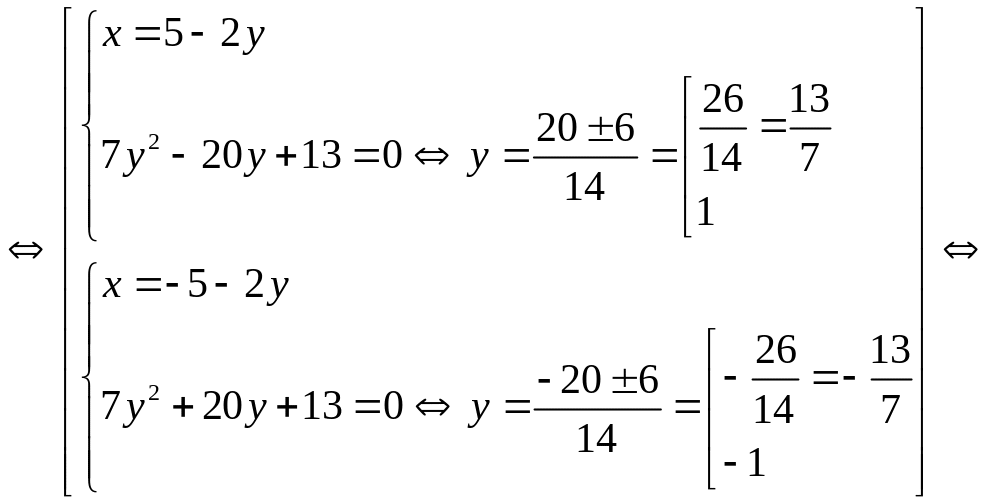
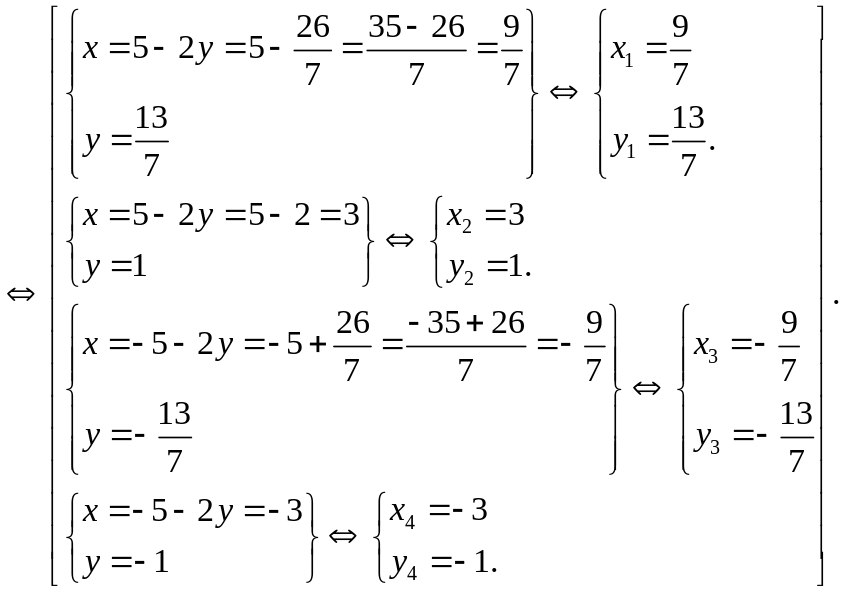
Система имеет четыре решения, которые подтверждаем проверкой, подставив каждое решение в оба уравнения исходной системы.

Проверка:

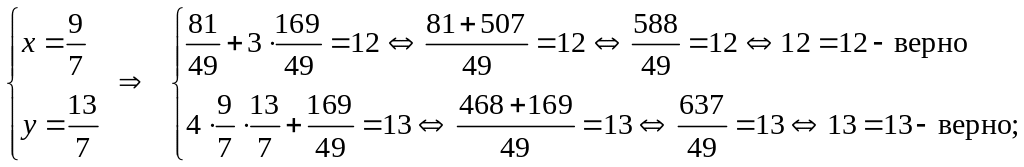
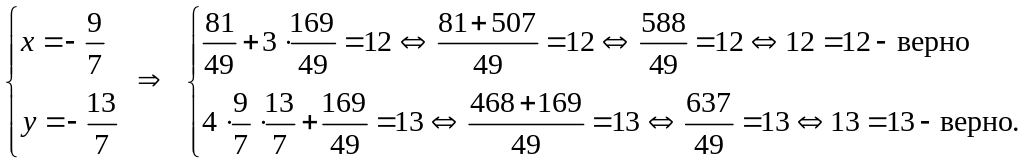
Ответ: , , , .

3. Введение вспомогательной неизвестной (частичная замена неизвестных)

ПРИМЕР

Решим систему уравнений

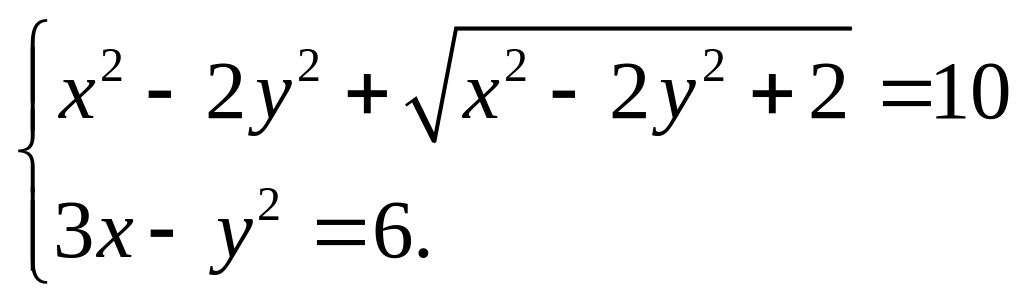
Решение

Введём в первом уравнении вспомогательную неизвестную , учитывая далее, что ; тогда в первом уравнении все слагаемые можно выразить через :

;

первое уравнение системы преобразуется к виду квадратного уравнения только относительно с ограничением на неизвестную:

.

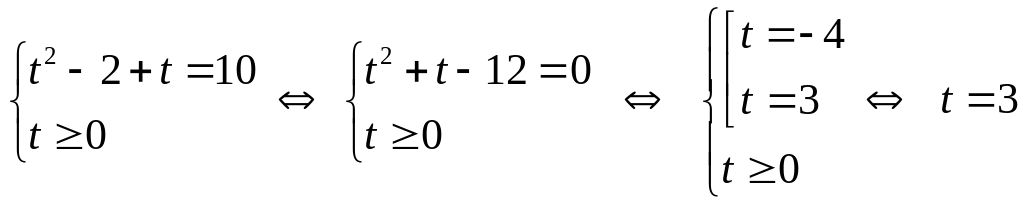Таким образом вычислено, что , и для этого вычисления использовано первое уравнение. Поэтому исходная система равносильна системе, в которой первое уравнение заменено на равенство , а второе уравнение оставлено прежним:

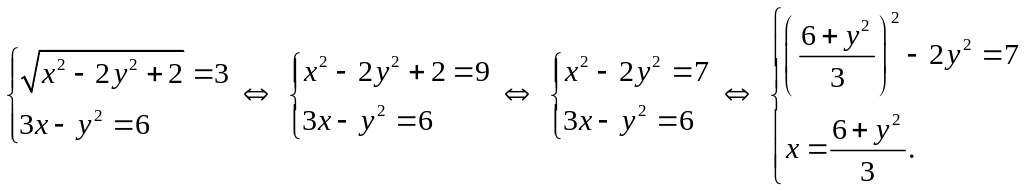
Выйдем теперь из системы с уравнением относительно у:

.

Возвращаемся в систему:

.

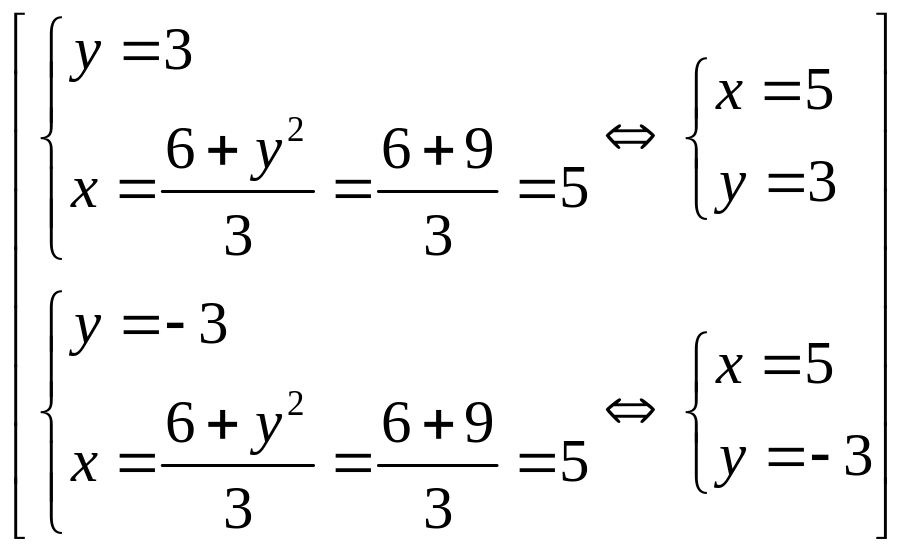Проверка:

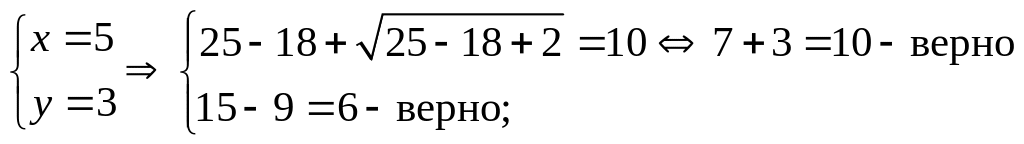
– эта пара удовлетворяет исходной системе, так как в систему входит только .

Ответ: , .

4. Полная замена неизвестных

ПРИМЕР

Решим следующую систему .

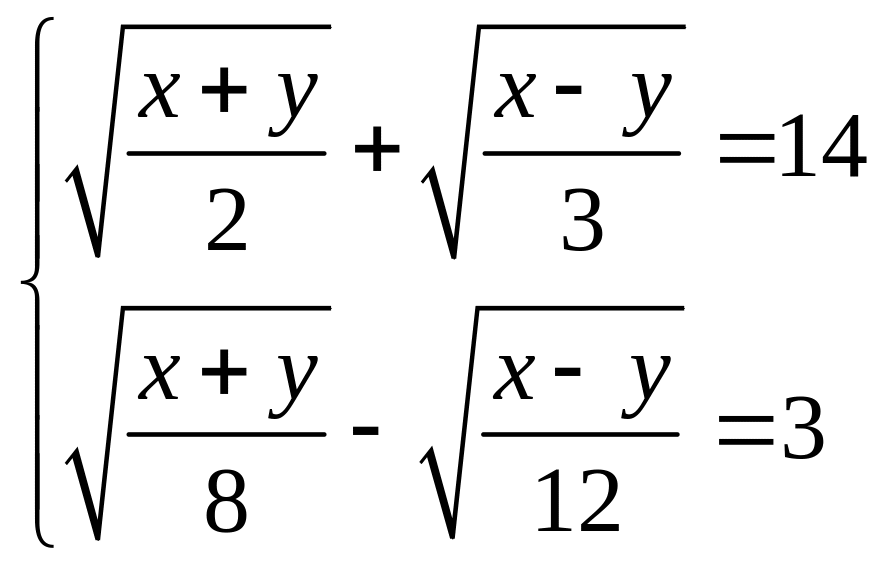Решение

Заменим две неизвестные х и у на две другие неизвестные u и v по формулам:

.

Тогда данная система относительно х,у преобразуется к равносильной системе относительно неизвестных u,v:

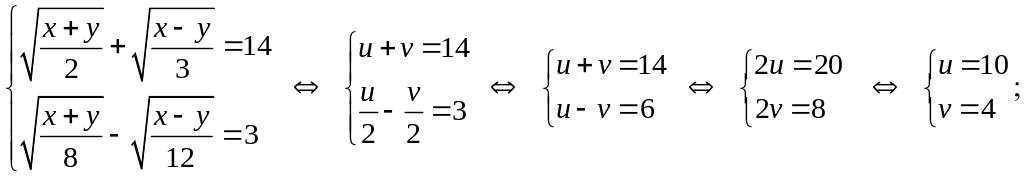
теперь выполняем обратную замену неизвестных:

.

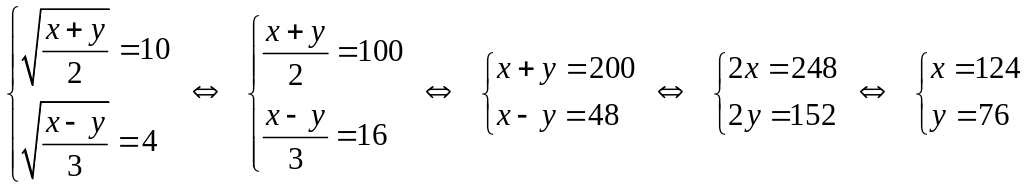Проверка:

Ответ: .