6.3. Бесконечно малые величины.

Функция называется бесконечно малой величиной при , или при , если ее предел равен нулю.

Функция называется бесконечно малой величиной при , если для любого, даже сколь угодно малого числа , найдется такое число (зависящее от ), что для всех и удовлетворяющих условию , будет верно неравенство .

Теорема. Если функция f(x) имеет при ( ) предел, равный А, то ее можно представить в виде суммы этого числа А и бесконечно малой при ( ).

.

Обратная теорема. Если функцию f(x) можно представить как сумму числа А и бесконечно малой при ( ), то число А есть предел этой функции при ( ).

Свойства бесконечно малых величин.

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию (в том числе на постоянную, на другую бесконечно малую) есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

6.4. Бесконечно большие величины.

Функция называется бесконечно большой величиной при или при , если ее предел равен бесконечности.

Определение. Функция называется бесконечно большой величиной при , если для любого, даже сколь угодно большого числа , найдется такое число (зависящее от ), что для всех и удовлетворяющих условию , будет верно неравенство .

Свойства бесконечно больших величин.

1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.

Связь между бесконечно малыми и бесконечно большими величинами.

Если функция есть бесконечно малая величина при ( ), то функция является бесконечно большой при ( ). И обратно, если функция есть бесконечно большая величина при ( ), то функция является бесконечно малой при ( ).

6.5. Основные теоремы о пределах. Признаки существования предела.

Пусть и – функции, для которых существуют пределы ( ): и

1. Функция не может иметь более одного предела.

2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. .

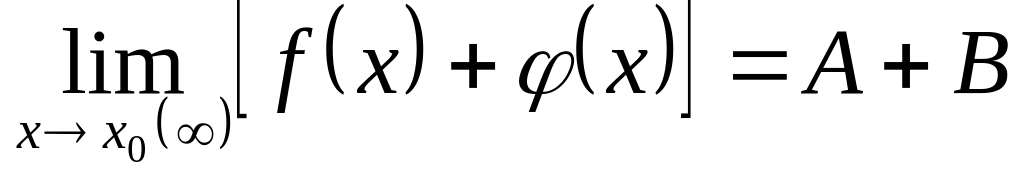3. Предел произведения конечного числа функций равен произведению пределов этих функций, т.е. .

4. Постоянный множитель можно выносить за знак предела.

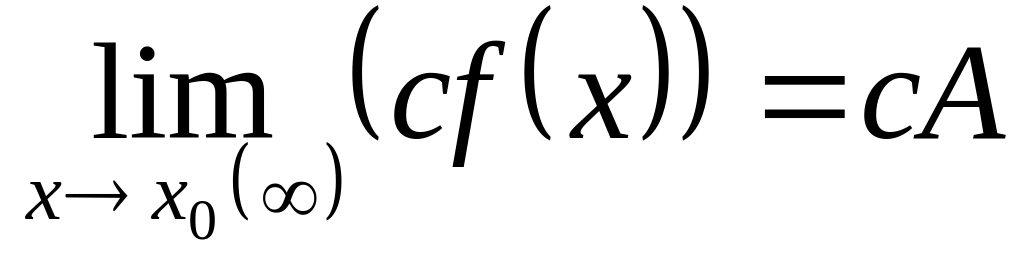
5. Предел частного двух функций равен частному пределов этих функций (при условии, что предел знаменателя не равен нулю), т.е. .

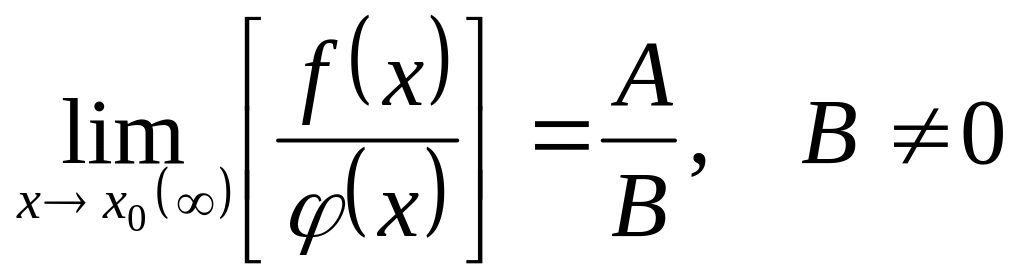6. Если , , 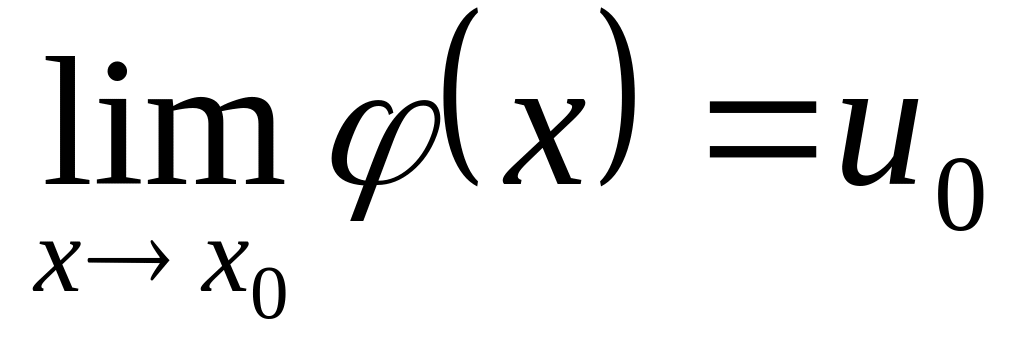то предел сложной функции .

7. Если в некоторой окрестности точки (или при достаточно больших значениях х) , то

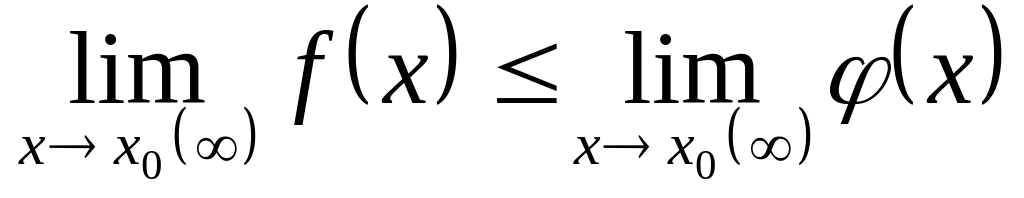
Теорема 1. Если числовая последовательность монотонна и ограниченна, то она имеет предел.

Теорема 2. Если в некоторой окрестности точки (или при достаточно больших значениях х) функция заключена между двумя функциями и , имеющими одинаковый предел А, то функция имеет тот же предел А