§4. Условная вероятность

Правило умножения вероятностей

Пусть А и В некоторые события, причем Р(В) > О. Условной вероятностью события А при условии В (обозначается Р(А |В)) называется вероятностью события А, найденная при условии, что событие В произошло. Эта вероятность находится по формуле

Аналогично определяется условная вероятность события В при условии А

Из этих формул следует:

Теорема 3. (Правило умножения вероятностей). Вероятность произведения двух событий равна произведению вероятности одного из них ин условную вероятность другого при условии, что первое событие произошло:

или

Понятие условной вероятности, так же как и правило умножения вероятностей, естественным образом обобщаются на случай произвольного числа событий. А именно, в случае п событий имеем

.

Независимые события

Событие А называется независимым от события В, если вероятность события А не зависит от того, осуществилось или нет событие В.

В этом случае условная вероятность события А при условии В равна безусловной вероятности события А, т. е. выполняется равенство .

Если событие А не зависит от события В то и событие В не зависит от А. Оба события при этом называются независимыми.

Таким образом, два события называются независимыми, если появление одного из них не меняет вероятности появления другого.

Для независимых событий правило умножения вероятностей принимает

Р(АВ) = P(А)· P(В).

Эта формула часто используется в качестве определения независимых событий.

События A₁, А₂, ..., А_n называются независимыми (или независимыми в совокупности), если вероятность каждого из них не зависит от осуществления или неосуществления любого числа остальных событий.

В случае п независимых событий имеем .

События A₁, А₂, ..., А_n называются попарно—независимыми, если любые два события A_i и А_j ( ) из этого набора независимы.

Независимые события A₁, А₂, ..., А_n являются попарно—независимыми. Обратное, вообще говоря, неверно.

Вероятность суммы совместных событий

Теорема 4. Вероятность суммы двух совместных событий есть сумма их вероятностей минус вероятность их произведения, т. е.

Р(А + В)= P(А) + P(D) - Р(АВ).

Для трех событий А, В и С имеем:

Р(А + В + С) = Р(А) + Р(В) + Р(С) — Р(АВ) – Р(АС) — Р(ВС) + Р(АВС).

В случае трех и большего числа событий для нахождения вероятности суммы S этих событий проще найти вероятность противоположного события , а затем воспользоваться равенством .

4.1. Брошены две игральные кости. Найти вероятность того, что на первой кости выпало 2 очка при условии, что сумма очков выпавших на двух костях меньше 6.

Решим задачу двумя способами.

1. Пусть событие А = {на первой кости выпало 2 очка}, событие В = {сумма очков, выпавших на двух костях меньше 6}. Событие В состоит из 10 элементарных событий:

В = ((1, 1), (1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (2, 2), (2,3), (3, 2)}.

Событие А, определяемое условием В (это значит, что исходы, благоприятствующие событию А, отбираются среди исходов, составляющих событие В), состоит из трех элементарных исходов опыта: (2,1), (2, 2), (2, 3). Поэтому искомая вероятность равна .

2. Пространство элементарных событий состоит из 36 элементов: Ω = {(1, 1), (1, 2), … , (6, 6)}. Для вычисления вероятности Р(А, В) воспользуемся формулой . Так как А = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2,6)},

В = {(1, 1), (1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (2, 2), (2, 3), (3, 2)}, то АВ ={(2, 1), (2, 2), (2, 3)}

По классическому определению вероятности , , . Поэтому

4.2. Из стандартного набора домино (28 штук) берется наудачу одна кость. Какова вероятность того что эта кость будет дублем (т.е. будет иметь вид 1—1, 4 – 4 и т.д.), если известно что сумма очков на ней четное число?

4.3. Найти вероятность того, что при бросании трех игральных костей хотя бы на одной выпадет 5 очков при условии, что на всех костях выпали грани с нечетным числом очков? с четным числом очков?

4.4. Вероятность попадания в цель равна 0,3, а вероятность ее уничтожения равна 0,05. Найти вероятность того, что при попадании в цель она будет уничтожена.

4.5. В произвольном порядке выписываются 2 буквы И и 2 буквы С. Найти вероятность того, что обе буквы С стоят рядом при условии, что последняя по порядку буква есть буква И.

4.6. Известно что события А и В независимы. Доказать, что события А и В также независимы.

О По условию . А так как , то ). Итак , т.е. события и В — независимы.

4.7. В урне находится 4 шара: красный, синий, черный и трехцветный (красно-сине-черный) шар. Из урны извлекается один шар. Исследовать на независимость события: К = {извлеченный шар имеет красный цвет}, С = {извлеченный шар имеет синий цвет}, Ч = {извлеченный шар имеет черный цвет}.

О Множество возможных исходов опыта таково: Ω = {К; С; Ч; КСЧ}, где буква К означает что извлечен шар красного цвета и т. д.

Очевидно, что .

Событиям К · С, К · Ч, С · Ч благоприятствует лишь один исход — это шар КСЧ (имеет все 3 цвета).

Значит , и .

Следовательно, события К и С, К и Ч, С и Ч независимы. Тем не менее, события К, С и Ч не являются независимыми в совокупности. Действительно, , а , т.е. .

4.8. Брошены три игральные кости. Событие А = {на 1-й и 2-й кости выпало одинаковое число очков}, событие В = {на 2-й и 3-й кости выпало одинаковое количество очков}, событие С = {на 1-й и 3й кости выпало одинаковое количество очков}. Будут ли события А, В и С:

а) попарно независимы;

б) независимы в совокупности?

4.9. Из колоды в 36 карт вытаскивается наудачу одна. Зависимы ли события А = {вытащен валет} и В = {вытащена карта черной масти}?

4.10. Доказать, что если события А и В независимы, то события и А, и также независимы.

4.11. В урне находится а белых и b черных шаров, причем а > 2 и b > 2. Из нее извлекаются два шара по схеме выбора с возвращением. Пусть событие А₁ = {первый шар белый}, А₂ = = {второй шар белый}. Найти Р(А₁), Р(А₂), Р(А₁ · А₂), Р(А₁│А₂) и Р(А₂│А₁). Выяснить: являются ли события А₁ и А₂ независимыми? совместными?

4.12. В урне 4 белых и 3 черных шара. Из нее вынимают 2 шара. Найти вероятность того, что оба шара белые. Рассмотреть выборки:

а) без возвращения; б) с возвращением.

О Пусть событие А₁ = {первый шар белый}, событие А₂ = {второй шар белый}. Тогда событие А = {оба шара белые} наступит, если осуществится и событие А₁ и событие А₂, т.е. А = А₁ · А₂.

а) События А₁ и А₂ зависимы, т. к. Наступление события А₁ влияет на вероятность события А₂ (шаров в урне останется 6, из них только 3 белых). Поэтому

б) Если после первого извлечения шар возвращается в урну, то события А₁ и А₂ — независимы, откуда

4.13. Задачу 3.6 решить другим способом используя правило умножения вероятностей для n событий.

О Рассмотрим следующие события: А = {получится слово АНАНАС}, А₁ = {первой, выбранной наудачу буквой, будет буква А}, А₂ = {второй – Н}, А₃ = {третьей А}, А₄ = {четвертой — Н}, А₅ = {пятой А}, А₆ = {шестой — С}. Тогда А = А₁ · А₂ · А₃ · А₄ · А₅ · А₆. Применяя правило умножения вероятностей, имеем

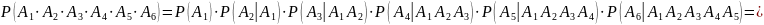
4.14. Из колоды в 36 карт наудачу вынимаются три карты (без возврата). Какова вероятность того, что среди них не будет ни одной шестерки?

4.15. Среди 100 лотерейных билетов есть 10 выигрышных. Какова вероятность того что 2 наудачу выбранных билета окажутся выигрышными?

4.16. Только один из 9 ключей подходит к данному замку. Как вероятность того, что придется опробовать 5 ключей для открывания замка?

4.17. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,3, второй — 0,4, третий – 0,5. По условиям приема события, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.

4.18. В ящике содержатся 9 белых, 6 черных и 5 зеленых шар. Наудачу вынимается один шар. Найти вероятность того, что он окажется либо черным либо зеленым.

О Пусть событие А = {извлеченный шар окажется черным}, В = {извлеченный шар окажется зеленым}, тогда событие С = {извлеченный шар окажется либо черным, либо зеленым} представляет собой сумму несовместных событий А и В, т. е. С = А + В. Поэтому

Вероятность извлечения черного или зеленого шара можно было бы найти без использования теоремы сложения вероятностей; ведь имеется 11 равновозможных благоприятных событию С исходов:

4.19. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания первого стрелка равна 0,7, а второго – 0,8. Найти вероятность того, что мишень будет поражена. А если стрелки делают по два выстрела?

О Пусть событие А_i = {попадание в мишень первым стрелком при i-м выстреле}, событие B_i = {попадание в мишень вторым стрелком при i-м выстреле}, i = 1, 2; событие С = {мишень поражена}.

Сначала решим задачу для случая, когда стрелки делают по одному выстрелу.

Первое решение. По условию Р(А₁) = Р(А₂) = 0,7, Р(В₁) = P(В₂) = 0,8.

Событие С = А₁ + В₁ состоит в том, что при одном залпе мишень будет поражена хотя бы одним стрелком.

Так как события А₁ и В₁ совместны, то Р(С) = Р(А₁ + В₁) = Р(А₁) + Р(В₁) — Р(А₁ · В₁).

События А₁ и В₁ независимы, поэтому Р(A₁ · В₁) = Р(А₁) · P(B₁), откуда

Р(С) = Р(А₁ + В₁) = Р(А₁) + Р(В₁) — Р(А₁ · В₁) = 0,7 + 0,8 — 0,7 · 0,8 = 0,94.

Второе решение.

Поражение цели (С) означает, что: в нее попал первый стрелок, а второй промазал ( ); или попал второй стрелок, а первый промазал ( ; или попали оба стрелка (А₁ · В₁). Тогда

По правилу сложения вероятностей несовместных событий получаем

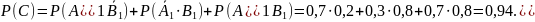
Третье решение.

Найдем вероятность события противоположного событию С. Очевидно, что = {оба стрелка промахнулись}. Так как события и независимы, то

Следовательно, Р(С) = 1 — Р ( ) = 1 — 0,06 = 0,94.

Если стрелки делают по два выстрела в мишень, то событию С благоприятствует 15 исходов данного опыта (стрельба по мишеням) из 16 возможных исходов. Такими исходами являются, например, следующие: , , , , и т.д. Поэтому проще найти вероятность противоположного события = {все четыре выстрела промах}. Имеем

Следовательно, Р(С) = 1—Р( ) = 1 — 0,003б = 0,9964.

4.20. Среди партии из 100 изделий имеется 10 бракованных. С целью контроля из этой партии отбираются наугад 7 изделий. Если среди них окажется более двух бракованных, то бракуется партия изделий. Какова вероятность того, что партия изделий будет забракована?

О Партия бракуется, если среди 7 изделий бракованными будет не менее трех; не бракуется, если среди 7 изделий бракованных ноль, одно или два.

Пусть событие А₀ = {среди 7 изделий нет бракованных}, событие А₁ = {среди 7 изделий есть одно бракованное}, событие А₂ = {среди 7 изделий — два бракованных}. Тогда событие А = {партия изделий принимается} можно представить в виде А = А₀ + А₁ + А₂. И так как события А₀, А₁, А₂ несовместны, то Р(А) = Р(А₀ + А₁ + А₂) = Р(А₀) + Р(А₁) + Р(А₂).

Найдем вероятность Р(А₀) используя классическое определение вероятности. Отобрать 7 деталей из 100 можно способами. Событию А₀ благоприятствует случаев. Следовательно, . Аналогично находим, что

Таким образом

Следовательно, вероятность того, что партия изделий будет забракована, равна Р( ) = 1 — Р(А) = = 1 — 0,98 = 0,02.

4.21. Один студент выучил 20 из 25 вопросов программы, а второй - только 15. Каждому из них задают по одному вопросу. Найти вероятность того, что правильно ответят:

а) оба студента; б) только первый студент;

в) только один из них; г) хотя бы один из студентов.

4.22. В одной комнате находятся 4 девушки и 7 юношей, в другой – 10 девушек и 5 юношей. Наудачу выбирают по одному человеку из каждой комнаты. Найти вероятность того, что оба окажутся юношами или оба — девушками.

4.23. Монета бросается до первого появления герба. Какова вероятность того, что понадобится четное число бросков?

4.24. При включении зажигания двигатель начнет работать с вероятностью 0,9. Какова вероятность того, что для запуска двигателя придется включать зажигание не более трех раз?

4.25. Электрическая цепь составлена по схеме, приведенной на рисунке 9. Элементы с номерами 1 2 3 могут выйти из строя независимо друг от друга с вероятностями, равными соответственно 0,10; 0,15; 0,20. Какова вероятность разрыва цепи?

Рис. 9

4.26. Устройство состоит из

а) пяти последовательно включенных элементов;

б) пяти параллельно включенных элементов.

Вероятность безотказной работы каждого из них равна 0,80. Определить вероятность безотказной работы всего устройства, полагая, что отказы отдельных элементов независимы.

4.27. Какова вероятность того, что наудачу написанную дробь :

а) можно сократить на 2; б) нельзя сократить на 6?

4.28. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Какова вероятность попадания при одном выстреле?